

10/11/2023

Làm sao để có câu trả lời hay nhất?
- Luôn có GIẢI THÍCH các bước giải
- Không copy câu trả lời của Timi
- Không sao chép trên mạng
- Không spam câu trả lời để nhận điểm
- Spam sẽ bị khóa tài khoản



10/11/2023

16/11/2023

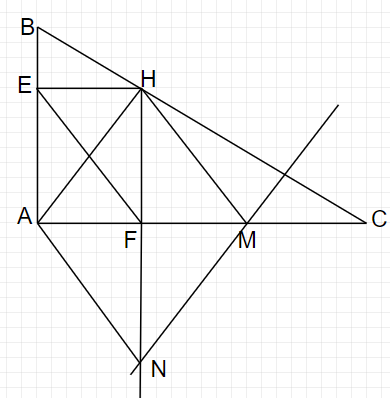
a) Xét tứ giác $\displaystyle AEHF$ có: $\displaystyle \widehat{EAF} =\widehat{AEH} =\widehat{AFH} =90^{0}$
$\displaystyle \Rightarrow AEHF$ là hình chữ nhật (dhnh)
b) $\displaystyle AEHF$ là hình chữ nhật nên $\displaystyle EH//AF$ và $\displaystyle EH=AF$
mà F là trung điểm của AM nên $\displaystyle AF=FM$
Do đó $\displaystyle EH//FM$ và $\displaystyle EH=FM$
Xét tứ giác $\displaystyle EFHM$ có: $\displaystyle EH//FM$ và $\displaystyle EH=FM$
$\displaystyle \Rightarrow EFHM$ là hình bình hành (dhnb)
c) Xét tứ giác $\displaystyle AEFN$ có $\displaystyle AE//FN( //HF)$ và $\displaystyle AE=FN( =HF)$
$\displaystyle \Rightarrow AEFN$ là hình bình hành (dhnb)
$\displaystyle \Rightarrow EF//AN$
Mà $\displaystyle EFHM$ là hình bình hành (cmt) $\displaystyle \Rightarrow EF//HM$
$\displaystyle \Rightarrow AN//HM( //EF)$
Xét tứ giác $\displaystyle AHMN$ có $\displaystyle AH//MN$ (gt)
$\displaystyle AN//HM$ (cmt)
$\displaystyle \Rightarrow AHMN$ là hình bình hành (dhnb)
Mà $\displaystyle AM\perp HN$ (gt)
$\displaystyle \Rightarrow AHMN$ là hình thoi (dhnb)

10/11/2023
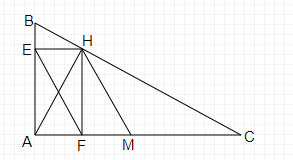
a, Vì $\displaystyle \vartriangle ABC$ vuông tại A nên $\displaystyle \widehat{EAF} =90^{0}$
Vì HE vuông góc AB tại E, HF vuông góc AC tại F nên $\displaystyle \widehat{AEH} =\widehat{AFH} =90^{0}$
Xét tứ giác AEHF có: $\displaystyle \widehat{EAF} =\ \widehat{AEH} =\widehat{AFH} =90^{0}$
$\displaystyle \Rightarrow $Tứ giác AEHF là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
Vậy tứ giác AEHF là hình chữ nhật
b, Vì tứ giác AEHF là hình chữ nhật nên $\displaystyle \begin{cases}
FM=EH & \\
FA\parallel EH &
\end{cases}$ (tính chất hình chữ nhật)
Vì F là trung điểm của AM nên $\displaystyle AF=FM$
Do đó $\displaystyle EH=FM$
Xét tứ giác EFMH có: $\displaystyle \begin{cases}
EH=FM & \\
EH\parallel FM\ ( do\ FA\parallel EH) &
\end{cases}$
Do đó tứ giác EFMH là hình bình hành (dấu hiệu nhận biết hình chữ nhật)
Đăng nhập hoặc Tạo tài khoản miễn phí!

 Điện thoại: 1900636019
Điện thoại: 1900636019
 Email: info@fqa.vn
Email: info@fqa.vn
LIÊN KẾT
- Hỏi đáp bài tập
- Giải bài tập SGK
- Cẩm nang
- Đề ôn luyện
- Điều khoản & chính sách
- Sitemap
- Liên hệ
- Đánh giá và góp ý
FQA.vn Nền tảng kết nối cộng đồng hỗ trợ giải bài tập học sinh trong khối K12. Sản phẩm được phát triển bởi CÔNG TY TNHH CÔNG NGHỆ GIA ĐÌNH (FTECH CO., LTD)
Copyright © 2025 fqa.vn All Rights Reserved












