Cho tam giác ABC vuông tại A , AB

Question

Cho tam giác ABC vuông tại A , AB < AC ,trung tuyến BN .Đường thẳng qua N // với BC cắt AB tại M đường thẳng qua N và vuông góc với AC cắt BC tại D
        a, tứ giác BMND là hình gì ? vì sao?
        b, biết BC = 10 cm . tính độ dài đoạn thẳng MN?
        c, trên tia đối của tia CA lấy điểm F sao cho CA = 2.CF . Trên BN lấy hai điểm l và E sao cho BI = IE = EN . Chứng minh rằng : AE , IF , BC đồng quy

Darlingg · Accepted Answer

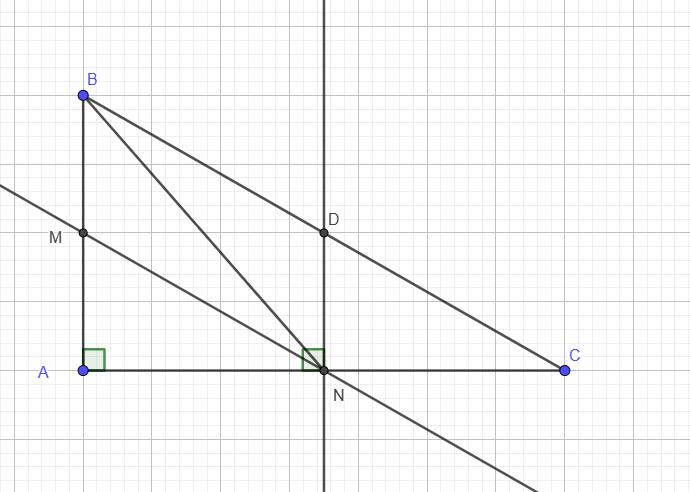
a) Có: $\displaystyle \Delta ABC$ vuông tại $\displaystyle A\Rightarrow AB\bot AC$
TĐB: $\displaystyle DN\bot AC$
$\displaystyle \Rightarrow AB//DN\ hay\ BM//DN$
TĐB: $\displaystyle MN//BC\Rightarrow MN//BD$
Tứ giác $\displaystyle BMND$ có:
$\displaystyle BM//DN$
$\displaystyle MN//BD$
$\displaystyle \Rightarrow BMND$ là hình bình hành.
b) Có $\displaystyle MN//BC$ mà $\displaystyle N$ là trung điểm $\displaystyle AC\Rightarrow M$ là trung điểm $\displaystyle AB$
$\displaystyle MN$ là đường trung bình $\displaystyle \Delta ABC$
$\displaystyle \Rightarrow MN=\frac{BC}{2} =\frac{10}{2} =5\ ( cm)$

Timi · Answer

1. Đây là một bài toán hình học trong tam giác vuông. Chúng ta cần sử dụng các định lý và quy tắc hình học để giải quyết bài toán này.

a. Để xác định loại hình của tứ giác BMND, ta cần phân tích các góc và cạnh của nó. Ta biết rằng tam giác ABC là tam giác vuông tại A, nên góc BAC = 90 độ. Vì BN là trung tuyến, nên NB = NC. Đường thẳng qua N song song với BC cắt AB tại M, và đường thẳng qua N vuông góc với AC cắt BC tại D.

Ta có:
   - Góc BNC = 180 - góc BAC (góc ngoài của tam giác ABC)
   - Góc BNM = góc BNC (vì BN là trung tuyến)
   - Góc BNM = góc BAC (vì góc BAC = 90 độ)
   - Góc BNM = 90 độ

Vậy tứ giác BMND là một hình chữ nhật vì có một góc vuông.

b. Để tính độ dài đoạn thẳng MN, ta cần sử dụng các quy tắc hình học và thông tin đã cho. Ta biết rằng BC = 10 cm và đường thẳng qua N // với BC.

Ta có:
   - Góc BNM = 90 độ (theo phần a)
   - Góc BNM = góc BAC = 90 độ (vì tam giác ABC là tam giác vuông tại A)

Vì đường thẳng qua N // với BC, ta có góc BNM = góc MBC (cặp góc đồng quy).

Vậy góc MBC = 90 độ.

Do đó, tam giác MBC cũng là tam giác vuông tại M.

Theo định lý Pythagoras, trong tam giác vuông MBC, ta có:

$MC^2 = MB^2 + BC^2$

$MC^2 = MB^2 + 10^2$

Ta cần tìm độ dài đoạn thẳng MN, nên ta cần tính độ dài của MC. Để làm điều này, ta cần biết độ dài của MB.

Tuy nhiên, thông tin về độ dài của MB không được cho trong đề bài. Vì vậy, không thể tính được độ dài đoạn thẳng MN.

c. Để chứng minh AE, IF, BC đồng quy, ta cần sử dụng các quy tắc hình học và thông tin đã cho.

Ta biết rằng trên tia đối của tia CA, ta lấy điểm F sao cho CA = 2CF. Trên BN, ta lấy hai điểm I và E sao cho BI = IE = EN.

Ta cần chứng minh rằng AE, IF, BC đồng quy. Để làm điều này, ta cần chứng minh rằng tứ giác AEIF là một tứ giác điều hòa.

Tuy nhiên, không có thông tin trong đề bài để chứng minh điều này. Vì vậy, không thể chứng minh AE, IF, BC đồng quy.

2. Do không có đủ thông tin trong đề bài để giải quyết các phần bài toán, chúng ta không thể tiến hành giải quyết từng bước cụ thể.

nguyễn đức chính 8A · Answer

{"userId":5120043,"userName":"Nguyễn Trinh"}

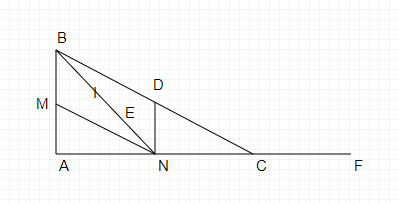
c,

Gọi giao điểm của hai đường chéo hình binh hành BMND là O

Xét tam giác ABC có BN là đường phân giác và BE=2/3 BN

Nên E là trọng tâm tam giác ABC

CMT ta có E thuộc MC

Mà AD là trung tuyến tam giác ABC (vì DN // AB , N là trung điểm AC)

Do đó A,E,D thẳng hàng

Xét tam giác INF có E là trung điểm IN (BI=IE=EN)và C là trung điểm NF(AC=2CF)

⇒EC là đường trung bình tam giác INF ⇒EC // DF(1)

Vì BMND là hình bình hành ⇒ BN cắt MD tại tung điểm mỗi đường hay OM=OD và OB=OM

Ta có E ∈ ON⇒OE+EN=ON

I∈BO⇒BI+IO=BO

Mà BO=ON và BI=EN Nên OI=OE

XÉT tứ giác IMED có MD cắt IE tại trung điểm O mỗi đường nên IMED là hình bình hành ⇒ME//ID hay EC//ID(2)

Từ (1)và (2)⇒I,D,F thẳng hàng

Ta có I,D,F thẳng hàng, và A,E,D thẳng hàng và D ∈ BC

⇒ AE, IF,BC đồng quy

CHÚC BẠN HỌC TỐT

sweettt · Answer

a.
N là trung điểm của AC (BN là trung tuyến)
MN//BD
$\displaystyle \begin{array}{{>{\displaystyle}l}}
DN\bot AC\
BM\bot AC\
\Rightarrow DN//BM
\end{array}$
Suy ra BMND là hình bình hành
b.
M là trung điểm của AC
MN//BC
Suy ra MN là đường trung bình
$\displaystyle \Rightarrow MN=\frac{BC}{2} =5( cm)$

Cho tam giác ABC vuông tại A , AB < AC ,trung tuyến BN .Đường thẳng qua N // với BC cắt AB tại M đường thẳng qua N và vuông góc với AC cắt BC tại D a, tứ giác BMND là hình gì ? vì sao? b, biết BC = 1...