giúp mk phần 3 thui ạ

Để giải quyết các mệnh đề về vận tốc và gia tốc của tàu con thoi, chúng ta sẽ sử dụng đạo hàm để phân tích các hàm số liên quan. Mệnh đề a) Vận tốc của tàu con thoi luôn tăng trong khoảng thời gian từ lúc cất cánh đến khi tên lửa đấy được phóng đi. Đạo hàm của hàm số vận tốc \( v(t) \): \[ v'(t) = \frac{d}{dt}(0,001302t^3 - 0,09029t^2 + 23,61t - 3,083) \] \[ v'(t) = 0,003906t^2 - 0,18058t + 23,61 \] Để kiểm tra xem vận tốc luôn tăng, ta cần kiểm tra dấu của đạo hàm \( v'(t) \) trong khoảng thời gian từ \( t = 0 \) đến \( t = 126 \). Tìm nghiệm của phương trình \( v'(t) = 0 \): \[ 0,003906t^2 - 0,18058t + 23,61 = 0 \] Sử dụng công thức nghiệm của phương trình bậc hai: \[ t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] \[ t = \frac{0,18058 \pm \sqrt{(0,18058)^2 - 4 \cdot 0,003906 \cdot 23,61}}{2 \cdot 0,003906} \] \[ t = \frac{0,18058 \pm \sqrt{0,03261 - 0,3716}}{0,007812} \] \[ t = \frac{0,18058 \pm \sqrt{-0,339}}{0,007812} \] Phương trình này không có nghiệm thực vì \( b^2 - 4ac < 0 \). Do đó, \( v'(t) \) luôn dương hoặc luôn âm trong khoảng \( t = 0 \) đến \( t = 126 \). Kiểm tra giá trị của \( v'(t) \) tại \( t = 0 \): \[ v'(0) = 23,61 > 0 \] Vì \( v'(t) \) luôn dương trong khoảng \( t = 0 \) đến \( t = 126 \), nên vận tốc của tàu con thoi luôn tăng. Mệnh đề a) đúng. Mệnh đề b) Gia tốc lớn nhất mà tàu con thoi có thể đạt được trong lúc thực hiện sứ mệnh trên (làm tròn đến hàng phần trăm) là 62,87 feet/s². Gia tốc \( a(t) \) là đạo hàm của vận tốc \( v(t) \): \[ a(t) = v'(t) = 0,003906t^2 - 0,18058t + 23,61 \] Đạo hàm của gia tốc \( a(t) \): \[ a'(t) = \frac{d}{dt}(0,003906t^2 - 0,18058t + 23,61) \] \[ a'(t) = 0,007812t - 0,18058 \] Tìm giá trị cực đại của \( a(t) \) bằng cách giải phương trình \( a'(t) = 0 \): \[ 0,007812t - 0,18058 = 0 \] \[ t = \frac{0,18058}{0,007812} \approx 23,11 \] Kiểm tra giá trị của \( a(t) \) tại \( t = 23,11 \): \[ a(23,11) = 0,003906 \cdot (23,11)^2 - 0,18058 \cdot 23,11 + 23,61 \] \[ a(23,11) \approx 62,87 \text{ feet/s}^2 \] Mệnh đề b) đúng. Mệnh đề c) Gia tốc của tàu con thoi tăng trong khoảng thời gian từ lúc cất cánh đến thời điểm \( t = 23 \) (s). Ta đã tìm được đạo hàm của gia tốc \( a'(t) \): \[ a'(t) = 0,007812t - 0,18058 \] Kiểm tra dấu của \( a'(t) \) trong khoảng \( t = 0 \) đến \( t = 23 \): \[ a'(0) = -0,18058 < 0 \] \[ a'(23) = 0,007812 \cdot 23 - 0,18058 \approx 0,000006 > 0 \] Do đó, \( a'(t) \) chuyển từ âm sang dương tại \( t = 23,11 \). Vì vậy, gia tốc của tàu con thoi tăng trong khoảng thời gian từ \( t = 0 \) đến \( t = 23 \). Mệnh đề c) đúng. Mệnh đề d) Gia tốc của tàu con thoi tăng trong khoảng thời gian từ \( t = 21,5 \) (s) đến 126 (s). Ta đã biết rằng \( a'(t) = 0,007812t - 0,18058 \). Kiểm tra dấu của \( a'(t) \) trong khoảng \( t = 21,5 \) đến \( t = 126 \): \[ a'(21,5) = 0,007812 \cdot 21,5 - 0,18058 \approx -0,000006 < 0 \] \[ a'(126) = 0,007812 \cdot 126 - 0,18058 \approx 0,800006 > 0 \] Do đó, \( a'(t) \) chuyển từ âm sang dương tại \( t = 23,11 \). Vì vậy, gia tốc của tàu con thoi tăng trong khoảng thời gian từ \( t = 23,11 \) đến 126. Mệnh đề d) đúng. Kết luận Các mệnh đề đúng là: - a) Vận tốc của tàu con thoi luôn tăng trong khoảng thời gian từ lúc cất cánh đến khi tên lửa đấy được phóng đi. - b) Gia tốc lớn nhất mà tàu con thoi có thể đạt được trong lúc thực hiện sứ mệnh trên (làm tròn đến hàng phần trăm) là 62,87 feet/s². - c) Gia tốc của tàu con thoi tăng trong khoảng thời gian từ lúc cất cánh đến thời điểm \( t = 23 \) (s). - d) Gia tốc của tàu con thoi tăng trong khoảng thời gian từ \( t = 21,5 \) (s) đến 126 (s). Câu 3: a) Đúng vì theo bảng biến thiên, hàm số có hai đường tiệm cận đứng là $x=-1$ và $x=1$. b) Sai vì theo bảng biến thiên, hàm số chỉ có một đường tiệm cận ngang là $y=2$. c) Đúng vì theo bảng biến thiên, hàm số nghịch biến trong khoảng $(1; +\infty)$. d) Đúng vì theo bảng biến thiên, hàm số có hai điểm cực trị là điểm cực đại và điểm cực tiểu. Câu 4: Để giải quyết câu hỏi này, chúng ta sẽ kiểm tra từng phát biểu một để xác định xem chúng đúng hay sai dựa vào đồ thị hàm số đã cho. a) Đồ thị hàm số đã cho là hàm số $y=\frac{2x^2-1}{x+1}.$ Để kiểm tra điều này, chúng ta cần vẽ đồ thị của hàm số $y=\frac{2x^2-1}{x+1}$ và so sánh nó với đồ thị đã cho. Tuy nhiên, vì chúng ta không có đồ thị cụ thể, chúng ta sẽ không thể xác nhận điều này chỉ dựa trên thông tin đã cho. Do đó, chúng ta sẽ tiếp tục kiểm tra các phát biểu khác trước. b) Hàm số đã cho không có giá trị lớn nhất và nhỏ nhất. Dựa vào đồ thị, chúng ta thấy rằng hàm số không có giới hạn trên hoặc dưới, nghĩa là nó không có giá trị lớn nhất và nhỏ nhất. Điều này đúng nếu đồ thị tiếp tục tăng hoặc giảm không giới hạn khi x tiến đến vô cùng hoặc âm vô cùng. c) Hàm số đã cho đồng biến trên R Dựa vào đồ thị, chúng ta thấy rằng hàm số không đồng biến trên toàn bộ tập xác định R. Có những đoạn trên đồ thị mà hàm số giảm, do đó phát biểu này là sai. d) Đồ thị hàm số đã cho có hai cực trị. Dựa vào đồ thị, chúng ta thấy rằng hàm số có hai điểm cực đại và cực tiểu, tức là hai cực trị. Điều này đúng nếu đồ thị có hai điểm uốn. Tóm lại, các phát biểu đúng là: - b) Hàm số đã cho không có giá trị lớn nhất và nhỏ nhất. - d) Đồ thị hàm số đã cho có hai cực trị. Đáp án: b) và d). Câu 1. 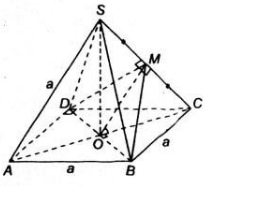Để tính góc giữa hai mặt phẳng (MBD) và (ABCD), ta thực hiện các bước sau: 1. Xác định đường thẳng giao của hai mặt phẳng: - Mặt phẳng (MBD) và (ABCD) giao nhau theo đường thẳng BD. 2. Tìm đường vuông góc hạ từ M xuống mặt phẳng (ABCD): - Vì S.ABCD là hình chóp đều, nên SO vuông góc với đáy ABCD. - Ta hạ đường vuông góc từ M xuống mặt phẳng (ABCD) tại điểm N. Đường thẳng này sẽ nằm trong mặt phẳng (SMO). 3. Tìm góc giữa hai mặt phẳng: - Góc giữa hai mặt phẳng (MBD) và (ABCD) chính là góc giữa đường thẳng MN và đường thẳng BD. 4. Tính toán chi tiết: - Ta biết rằng SO vuông góc với đáy ABCD, do đó SO vuông góc với BD. - Mặt khác, vì M là trung điểm của SC, nên MN cũng sẽ vuông góc với BD (do MN nằm trong mặt phẳng (SMO) và SO vuông góc với BD). 5. Xác định góc giữa MN và BD: - Gọi H là trung điểm của BD. Ta có: \[ SH \perp BD \quad \text{(vì S.ABCD là hình chóp đều)} \] - Do đó, góc giữa MN và BD chính là góc giữa MN và SH. 6. Tính toán góc này: - Ta biết rằng SO = a (do S.ABCD là hình chóp đều và các cạnh bên bằng a). - Vì M là trung điểm của SC, nên MN = $\frac{SO}{2} = \frac{a}{2}$. - Ta cũng biết rằng SH = $\frac{a\sqrt{2}}{2}$ (do BD là đường chéo của hình vuông ABCD và BD = a√2). 7. Tính góc giữa MN và SH: - Gọi góc giữa MN và SH là $\theta$. Ta có: \[ \sin(\theta) = \frac{MN}{SH} = \frac{\frac{a}{2}}{\frac{a\sqrt{2}}{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \] - Vậy $\theta = 45^\circ$. Do đó, góc giữa hai mặt phẳng (MBD) và (ABCD) là 45°. Đáp số: 45° Câu 2: Trước hết, chúng ta cần xác định hàm số \( f(t) \) biểu thị nồng độ muối trong bể sau \( t \) phút. Số lượng nước muối đã bơm vào bể sau \( t \) phút là: \[ 20t \text{ lít} \] Số lượng muối trong nước muối đã bơm vào bể sau \( t \) phút là: \[ 25 \times 20t = 500t \text{ gam} \] Tổng thể tích nước trong bể sau \( t \) phút là: \[ 3000 + 20t \text{ lít} \] Nồng độ muối trong bể sau \( t \) phút là: \[ f(t) = \frac{500t}{3000 + 20t} \text{ gam/lít} \] Bây giờ, chúng ta cần tìm giới hạn của hàm số \( f(t) \) khi \( t \) tiến đến vô cùng: \[ \lim_{t \to +\infty} f(t) = \lim_{t \to +\infty} \frac{500t}{3000 + 20t} \] Chia cả tử và mẫu cho \( t \): \[ \lim_{t \to +\infty} \frac{500t}{3000 + 20t} = \lim_{t \to +\infty} \frac{500}{\frac{3000}{t} + 20} \] Khi \( t \) tiến đến vô cùng, \(\frac{3000}{t}\) tiến đến 0: \[ \lim_{t \to +\infty} \frac{500}{\frac{3000}{t} + 20} = \frac{500}{0 + 20} = \frac{500}{20} = 25 \text{ gam/lít} \] Vậy khi \( t \) càng lớn, nồng độ muối trong bể tiến gần đến 25 gam/lít. Đáp số: 25 gam/lít. Câu 3. Để giải quyết bài toán này, chúng ta cần tìm khoảng thời gian mà tốc độ truyền bệnh giảm. Tốc độ truyền bệnh được xác định bởi đạo hàm của hàm số \( f(t) \). Bước 1: Tìm đạo hàm của \( f(t) \). \[ f(t) = 45t^2 - t^3 \] \[ f'(t) = \frac{d}{dt}(45t^2 - t^3) = 90t - 3t^2 \] Bước 2: Xác định khoảng thời gian mà tốc độ truyền bệnh giảm. Tốc độ truyền bệnh giảm khi đạo hàm \( f'(t) \) giảm, tức là đạo hàm của \( f'(t) \) là âm. \[ f''(t) = \frac{d}{dt}(90t - 3t^2) = 90 - 6t \] Để \( f''(t) < 0 \): \[ 90 - 6t < 0 \] \[ 90 < 6t \] \[ t > 15 \] Bước 3: Xác định khoảng thời gian mà tốc độ truyền bệnh giảm. Từ bước 2, ta thấy tốc độ truyền bệnh giảm khi \( t > 15 \). Do đó, khoảng thời gian mà tốc độ truyền bệnh giảm là từ ngày thứ 16 đến ngày thứ 25. Bước 4: Tính \( n - m \). Trong bài toán này, \( m = 16 \) và \( n = 25 \). \[ n - m = 25 - 16 = 9 \] Vậy, \( n - m = 9 \). Đáp số: \( n - m = 9 \). Câu 4. Trước tiên, ta sẽ phân tích các vectơ trong đẳng thức: \[ \overrightarrow{AB} + \overrightarrow{B_1C_1} + \overrightarrow{DD_1} = k \overrightarrow{AC_1} \] 1. Ta biết rằng trong hình hộp, các cạnh song song và bằng nhau. Do đó: - $\overrightarrow{AB} = \overrightarrow{DC}$ - $\overrightarrow{B_1C_1} = \overrightarrow{A_1D_1}$ - $\overrightarrow{DD_1} = \overrightarrow{AA_1}$ 2. Ta cũng biết rằng trong hình hộp, các vectơ từ đỉnh A đến các đỉnh khác có thể được viết dưới dạng tổng của các vectơ cơ bản. Cụ thể: - $\overrightarrow{AC_1} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1}$ 3. Bây giờ, ta thay các vectơ tương ứng vào đẳng thức ban đầu: \[ \overrightarrow{AB} + \overrightarrow{B_1C_1} + \overrightarrow{DD_1} = \overrightarrow{AB} + \overrightarrow{A_1D_1} + \overrightarrow{AA_1} \] 4. Vì $\overrightarrow{A_1D_1} = \overrightarrow{AD}$, nên ta có: \[ \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1} \] 5. So sánh với $\overrightarrow{AC_1} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1}$, ta thấy rằng: \[ \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA_1} = \overrightarrow{AC_1} \] 6. Do đó, ta có: \[ \overrightarrow{AB} + \overrightarrow{B_1C_1} + \overrightarrow{DD_1} = \overrightarrow{AC_1} \] Từ đây, ta suy ra: \[ k = 1 \] Vậy giá trị của \( k \) là: \[ \boxed{1} \] Câu 5. Để giải bài toán này, chúng ta cần tìm điểm M trên đường bờ biển sao cho tổng thời gian chạy từ X qua M, rồi từ M qua N và cuối cùng từ N đến Y là ngắn nhất. Điều này sẽ làm giảm thời gian bị rắn cắn, do đó giảm nồng độ chất độc trong máu. Bước 1: Xác định các đoạn đường và vận tốc. - Vận tốc trong rừng: 5 km/h. - Vận tốc trên đường bờ biển: 13 km/h. - Đoạn đường từ X đến M: $\sqrt{x^2 + 3^2} = \sqrt{x^2 + 9}$ km. - Đoạn đường từ M đến N: $(18 - 2x)$ km. - Đoạn đường từ N đến Y: $\sqrt{x^2 + 3^2} = \sqrt{x^2 + 9}$ km. Bước 2: Tính tổng thời gian chạy. Thời gian chạy từ X đến M: \[ t_1 = \frac{\sqrt{x^2 + 9}}{5} \] Thời gian chạy từ M đến N: \[ t_2 = \frac{18 - 2x}{13} \] Thời gian chạy từ N đến Y: \[ t_3 = \frac{\sqrt{x^2 + 9}}{5} \] Tổng thời gian chạy: \[ T = t_1 + t_2 + t_3 = \frac{\sqrt{x^2 + 9}}{5} + \frac{18 - 2x}{13} + \frac{\sqrt{x^2 + 9}}{5} = \frac{2\sqrt{x^2 + 9}}{5} + \frac{18 - 2x}{13} \] Bước 3: Tìm giá trị của \( x \) để tổng thời gian chạy \( T \) là nhỏ nhất. Để tối thiểu hóa \( T \), chúng ta sẽ tìm đạo hàm của \( T \) theo \( x \) và đặt nó bằng 0. \[ T = \frac{2\sqrt{x^2 + 9}}{5} + \frac{18 - 2x}{13} \] Đạo hàm của \( T \): \[ \frac{dT}{dx} = \frac{2}{5} \cdot \frac{x}{\sqrt{x^2 + 9}} - \frac{2}{13} \] Đặt đạo hàm bằng 0: \[ \frac{2}{5} \cdot \frac{x}{\sqrt{x^2 + 9}} = \frac{2}{13} \] \[ \frac{x}{\sqrt{x^2 + 9}} = \frac{5}{13} \] \[ 13x = 5\sqrt{x^2 + 9} \] \[ 169x^2 = 25(x^2 + 9) \] \[ 169x^2 = 25x^2 + 225 \] \[ 144x^2 = 225 \] \[ x^2 = \frac{225}{144} \] \[ x = \frac{15}{12} = \frac{5}{4} = 1.25 \] Bước 4: Tính tổng thời gian chạy khi \( x = 1.25 \). \[ T = \frac{2\sqrt{(1.25)^2 + 9}}{5} + \frac{18 - 2(1.25)}{13} \] \[ T = \frac{2\sqrt{1.5625 + 9}}{5} + \frac{18 - 2.5}{13} \] \[ T = \frac{2\sqrt{10.5625}}{5} + \frac{15.5}{13} \] \[ T = \frac{2 \times 3.25}{5} + \frac{15.5}{13} \] \[ T = \frac{6.5}{5} + \frac{15.5}{13} \] \[ T = 1.3 + 1.1923 \approx 2.4923 \text{ giờ} \] Bước 5: Tính nồng độ chất độc trong máu khi về đến trại. \[ y = 50 \log(t + 2) \] \[ y = 50 \log(2.4923 + 2) \] \[ y = 50 \log(4.4923) \] \[ y \approx 50 \times 0.6525 \] \[ y \approx 32.625 \] Vậy nồng độ chất độc trong máu thấp nhất khi ông An về đến trại là khoảng 32.6 mg/l (làm tròn đến hàng phần chục). Câu 6. Trước hết, ta cần xác định tổng trọng lượng của khung sắt và chiếc xe ô tô: \[ W_{\text{tổng}} = W_{\text{sắt}} + W_{\text{ô tô}} = 1000 \, \text{N} + 4000 \, \text{N} = 5000 \, \text{N} \] Do các đoạn dây cáp EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc \(45^\circ\), nên lực căng của mỗi đoạn dây cáp sẽ là một phần của tổng trọng lượng này. Ta có 4 đoạn dây cáp, do đó mỗi đoạn dây cáp chịu một phần tư tổng trọng lượng: \[ F_{\text{căng}} = \frac{W_{\text{tổng}}}{4} = \frac{5000 \, \text{N}}{4} = 1250 \, \text{N} \] Tuy nhiên, vì các đoạn dây cáp tạo với mặt phẳng (ABCD) một góc \(45^\circ\), nên lực căng thực tế của mỗi đoạn dây cáp sẽ là: \[ F_{\text{căng thực tế}} = \frac{F_{\text{căng}}}{\cos(45^\circ)} = \frac{1250 \, \text{N}}{\frac{\sqrt{2}}{2}} = 1250 \times \sqrt{2} \approx 1768 \, \text{N} \] Vậy cường độ lực căng của mỗi đoạn dây cáp là: \[ \boxed{1768 \, \text{N}} \]