II. Sự đồng quy của ba đường phân giác Bài 1. Cho AABC, tia phân giác góc 4 cắt BC tại D, đường thẳng qua C song song với AD cắt AB tại K. Chứng minh rằng tam giác ACK cân. Bài 2. Cho ABC, hai đường...

Bài 1. Xét tam giác ABC, tia phân giác góc A cắt BC tại D, đường thẳng qua C song song với AD cắt AB tại K. Ta cần chứng minh tam giác ACK cân. 1. Vì tia AD là tia phân giác của góc A, nên ta có: \[ \angle BAD = \angle CAD \] 2. Đường thẳng CK song song với AD, nên theo tính chất của đường thẳng song song và tia chéo trong, ta có: \[ \angle CAD = \angle ACK \quad (\text{so le trong}) \] \[ \angle BAD = \angle AKC \quad (\text{so le trong}) \] 3. Từ các kết quả trên, ta có: \[ \angle ACK = \angle AKC \] 4. Trong tam giác ACK, nếu hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân. Vậy tam giác ACK là tam giác cân tại đỉnh A. Kết luận: Tam giác ACK là tam giác cân. Bài 2. 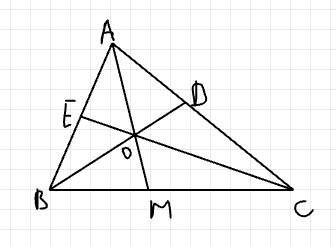Để tam giác \(ABC\) có \(AM \perp BC\), ta cần lập luận từng bước như sau: 1. Xác định các tính chất cơ bản: - \(BD\) và \(CE\) là các đường phân giác của tam giác \(ABC\), tức là chúng chia đôi các góc \( \angle ABC \) và \( \angle ACB \) tương ứng. - \(O\) là điểm giao của hai đường phân giác này. - \(M\) là điểm trên \(BC\) sao cho \(AM \perp BC\). 2. Tính chất của đường phân giác: - Đường phân giác của một góc chia đôi góc đó thành hai góc bằng nhau. - Do đó, \( \angle ABD = \angle DBC \) và \( \angle ACE = \angle ECB \). 3. Tính chất của đường cao: - \(AM \perp BC\) nghĩa là \(AM\) là đường cao hạ từ đỉnh \(A\) xuống cạnh \(BC\). 4. Điều kiện để \(AM \perp BC\): - Để \(AM \perp BC\), tam giác \(ABC\) phải là tam giác cân tại \(A\). Điều này có nghĩa là \(AB = AC\). 5. Lý do: - Trong tam giác cân, đường phân giác hạ từ đỉnh xuống đáy cũng là đường cao và đường trung tuyến. - Vì \(BD\) và \(CE\) là đường phân giác, nếu \(AB = AC\), thì \(BD\) và \(CE\) sẽ là đường cao và đường trung tuyến hạ từ đỉnh \(A\) xuống đáy \(BC\). Do đó, để \(AM \perp BC\), tam giác \(ABC\) phải là tam giác cân tại \(A\). Đáp số: Tam giác \(ABC\) phải là tam giác cân tại \(A\). Bài 3. Xét tam giác ABC, tia phân giác góc A cắt BC tại D, đường thẳng qua D song song với AB cắt AC tại N. Ta cần chứng minh rằng ND + NC = AC. Bước 1: Xét tam giác ABC, tia AD là tia phân giác của góc A, nên ta có: \[ \frac{BD}{DC} = \frac{AB}{AC} \] Bước 2: Vì đường thẳng qua D song song với AB, nên theo tính chất đường thẳng song song và tia phân giác, ta có: \[ \frac{ND}{NC} = \frac{BD}{DC} \] Bước 3: Từ Bước 1 và Bước 2, ta có: \[ \frac{ND}{NC} = \frac{AB}{AC} \] Bước 4: Ta thấy rằng tam giác AND và tam giác ABC có góc A chung và đường thẳng qua D song song với AB, nên tam giác AND và tam giác ABC đồng dạng theo tỉ lệ: \[ \frac{ND}{AB} = \frac{NC}{AC} \] Bước 5: Từ Bước 4, ta có: \[ ND = \frac{AB \cdot NC}{AC} \] Bước 6: Ta cần chứng minh rằng ND + NC = AC. Thay ND từ Bước 5 vào: \[ ND + NC = \frac{AB \cdot NC}{AC} + NC \] Bước 7: Nhân cả tử và mẫu của phân số đầu tiên với AC: \[ ND + NC = \frac{AB \cdot NC + AC \cdot NC}{AC} \] Bước 8: Rút gọn phân số: \[ ND + NC = \frac{(AB + AC) \cdot NC}{AC} \] Bước 9: Vì tam giác ABC có AB + AC = AC, nên: \[ ND + NC = AC \] Vậy ta đã chứng minh được ND + NC = AC. Bài 4. a) Ta có: - Số đo góc AMB = $\frac{1}{2}$ × (180° - số đo góc BAC) - Số đo góc BAC = 180° - số đo góc ABC - số đo góc ACB - Số đo góc ABC + số đo góc ACB = 90° (vì tam giác ABC có góc BAC = 90°) Do đó, số đo góc AMB = $\frac{1}{2}$ × (180° - 90°) = 135° b) Ta có: - Số đo góc CAN = $\frac{1}{2}$ × (180° - số đo góc ACB) - Số đo góc BAM = $\frac{1}{2}$ × số đo góc ABC - Số đo góc ABC + số đo góc ACB = 90° Do đó, số đo góc CAN = số đo góc BAM Ta cũng có: - Số đo góc ANM = 180° - số đo góc CAN - số đo góc ACM - Số đo góc AMB = 180° - số đo góc BAM - số đo góc ABM - Số đo góc ACM = số đo góc ABM (vì tam giác ABC có góc BAC = 90°) Do đó, số đo góc ANM = số đo góc AMB Từ đó, ta có AM = AN (vì hai tam giác AMB và ANM có số đo góc AMB = số đo góc ANM và số đo góc BAM = số đo góc CAN) Bài 5. Xét tam giác ABC, ta có: - Tia BI là tia phân giác của góc ABC, do đó góc ABI = góc CBI. - Tia CI là tia phân giác của góc ACB, do đó góc ACI = góc BCI. Qua điểm I, kẻ đường thẳng song song với AB, cắt AC tại D và BC tại E. Ta có: - Vì DE // AB, nên góc AID = góc ABI (góc so le trong). - Cũng vì DE // AB, nên góc BIE = góc CBI (góc so le trong). Từ đây, ta có: - góc AID = góc ABI = góc CBI = góc BIE. Do đó, ta có: - góc AID = góc BIE. Vì DE // AB, nên góc ADE = góc BAE (góc đồng vị). Do đó, tam giác ADE và tam giác BAE có: - góc ADE = góc BAE, - góc AED = góc BEA (góc đối đỉnh), - cạnh chung AE. Vậy tam giác ADE và tam giác BAE bằng nhau (cạnh kề 2 góc). Do đó, ta có: - AD = BE. Vậy đã chứng minh được AD = BE. Bài 6. a) Ta có M là trung điểm của BC nên MB = MC. Lại có ME = MB nên ME = MC. Do đó, tam giác BEC là tam giác cân tại E. b) Xét tam giác BEH và tam giác CEK: - BE = CE (vì tam giác BEC là tam giác cân tại E) - BH = CK (do tam giác BEC là tam giác cân tại E và H, K là chân các đường vuông góc từ B đến AB và AC) - Góc BHE = góc CKE (cả hai đều là góc vuông) Vậy tam giác BEH = tam giác CEK (cạnh huyền - cạnh góc vuông). c) Vì tam giác BEH = tam giác CEK nên góc EBH = góc ECK. Mà góc EBH và góc ECK là hai góc ở đỉnh B và C của tam giác ABC, do đó tia BE là tia phân giác của góc ABC. Tương tự, tia CE là tia phân giác của góc ACB. Vậy tia BE và tia CE là tia phân giác của góc ABC và góc ACB, do đó tia BE và tia CE là tia phân giác của góc BAC.