hộ bài này với ạ

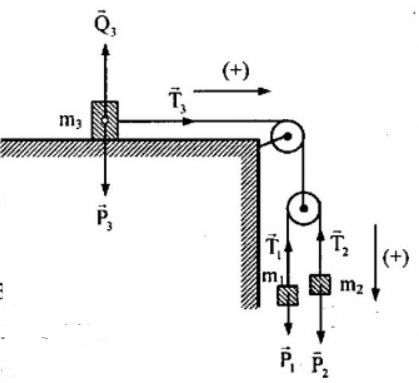
Gọi $\vec{a}_0$ là gia tốc ròng rọc động đối với mặt đất; $\vec{a}_1$, $\vec{a}_2$ lần lượt là gia tốc của vật $m_1, m_2$ đối với ròng rọc. Theo công thức cộng gia tốc:
$
\vec{a}_3=-\vec{a}_0 ; \vec{a}_1=\vec{a}_1^{\prime}+\vec{a}_0 ; \vec{a}_2=\vec{a}_2+\vec{a}_0
$

Áp dụng định luật II Niu-tơn cho từng vật:
$
\begin{aligned}
& \overrightarrow{\mathrm{T}}_3+\overrightarrow{\mathrm{P}}_3+\overrightarrow{\mathrm{Q}}_3=\mathrm{m}_3 \overrightarrow{\mathrm{a}} \\
& \overrightarrow{\mathrm{P}}_1+\overrightarrow{\mathrm{T}}_1=\mathrm{m}_1 \overrightarrow{\mathrm{a}}_1 \\
& \overrightarrow{\mathrm{P}}_2+\overrightarrow{\mathrm{T}}_2=\mathrm{m}_2 \overrightarrow{\mathrm{a}}_2
\end{aligned}
$

Chiếu (1) lên chiều chuyển động của $\mathrm{m}_3$ ta được:
$
\mathrm{T}_3=\mathrm{m}_3 \mathrm{a}_3=\mathrm{m}_3 \mathrm{a}_0
$

Chiếu (2), (3) lên phương thẳng đứng, chiều dương hướng xuống dươi, ta được:
$
\begin{aligned}
& \mathrm{P}_1-\mathrm{T}_1=\mathrm{m}_1 \mathrm{a}_1 \Rightarrow \mathrm{P}_1-\mathrm{T}_1=\mathrm{m}_1\left(\mathrm{a}_1+\mathrm{a}_0\right) \\
& \mathrm{P}_2-\mathrm{T}_2=\mathrm{m}_2 \mathrm{a}_2 \Rightarrow \mathrm{P}_2-\mathrm{T}_2=\mathrm{m}_2\left(\mathrm{a}_2+\mathrm{a}_0\right)
\end{aligned}
$

Vì dây không dãn, bỏ qua khối lượng của ròng rọc nên:
$
\mathrm{a}_1^{\prime}=-\mathrm{a}_2, \mathrm{~T}_1=\mathrm{T}_2 \Rightarrow \mathrm{T}_3=2 \mathrm{~T}_1 \text {. }
$

Từ (5) và (6) ta được: $\mathrm{P}_1-\mathrm{P}_2=\mathrm{m}_1\left(\mathrm{a}_1^{\prime}+\mathrm{a}_0\right)-\mathrm{m}_2\left(\mathrm{a}_2^{\prime}+\mathrm{a}_0\right)$
$
\Rightarrow\left(m_1-m_2\right) g=\left(m_1-m_2\right) a_0+\left(m_1+m_2\right) a_1^{\prime}
$

Lấy (4) cộng (5) ta được: $\mathrm{m}_1 \mathrm{~g}=\frac{\mathrm{m}_3 \mathrm{a}_0}{2}+\mathrm{m}_1\left(\mathrm{a}_1^{\prime}+\mathrm{a}_0\right)$
$
\begin{aligned}
& \Rightarrow m_1 g=\left(\frac{m_3}{2}+m_1\right) a_0+m_1 a_1^{\prime} \\
& \Rightarrow a_1^{\prime}=g-\left(\frac{m_3}{2 m_1}+1\right) a_0
\end{aligned}
$

Thay (8) vào (7) ta được:
$
\begin{aligned}
& \left(m_1-m_2\right) g=\left(m_1-m_2\right) a_0+\left(m_1+m_2\right)\left[g-\left(\frac{m_3}{2 m_1}+1\right) a_0\right] \\
& \Rightarrow\left[m_2-m_1+\left(m_1+m_2\right)\left(\frac{m_3}{2 m_1}+1\right)\right] a_0=\left(m_2-m_1+m_1+m_2\right) g \\
& \Rightarrow a_0=\frac{4 m_1 m_2 g}{4 m_1 m_2+m_3\left(m_1+m_2\right)}=\frac{4.1 .2 .10}{41.2+4(1+2)}=4 \mathrm{~m} / \mathrm{s}^2
\end{aligned}
$

Thay $\mathrm{a}_0$ vào (8) ta được: $\mathrm{a}_1^{\prime}=\mathrm{g}-\left(\frac{\mathrm{m}_3}{2 \mathrm{~m}_1}+1\right) \mathrm{a}_0=10-\left(\frac{4}{2.1}+1\right)=-2 \mathrm{~m} / \mathrm{s}^2$
Gia tốc của vật $1: a_1=a_1^{\prime}+a_0=-2+4=2 \mathrm{~m} / \mathrm{s}^2$
Vậy: Gia tốc của $\mathrm{m}_1$ là $\mathrm{a}_1=2 \mathrm{~m} / \mathrm{s}^2$.