Câu 3.
Để giải quyết câu hỏi này, chúng ta sẽ kiểm tra từng phần một cách chi tiết.
a) Hàm số có 2 điểm cực trị.
Đầu tiên, ta tìm đạo hàm của hàm số \( y = \frac{x^2 + 2x - 1}{x - 1} \):
\[ y' = \frac{(x^2 + 2x - 1)'(x - 1) - (x^2 + 2x - 1)(x - 1)'}{(x - 1)^2} \]
\[ y' = \frac{(2x + 2)(x - 1) - (x^2 + 2x - 1)}{(x - 1)^2} \]
\[ y' = \frac{2x^2 + 2x - 2x - 2 - x^2 - 2x + 1}{(x - 1)^2} \]
\[ y' = \frac{x^2 - 2x - 1}{(x - 1)^2} \]
Để tìm điểm cực trị, ta giải phương trình \( y' = 0 \):
\[ \frac{x^2 - 2x - 1}{(x - 1)^2} = 0 \]
\[ x^2 - 2x - 1 = 0 \]
Phương trình này có hai nghiệm thực:
\[ x = 1 + \sqrt{2} \quad \text{và} \quad x = 1 - \sqrt{2} \]
Vậy hàm số có 2 điểm cực trị. Đáp án đúng.
b) Đồ thị (C) có tiệm cận đứng là đường thẳng có phương trình \( x = 1 \).
Tiệm cận đứng của hàm số \( y = \frac{x^2 + 2x - 1}{x - 1} \) là giá trị của \( x \) làm mẫu số bằng 0:
\[ x - 1 = 0 \Rightarrow x = 1 \]
Vậy đồ thị (C) có tiệm cận đứng là đường thẳng \( x = 1 \). Đáp án đúng.
c) Hàm số nghịch biến trên khoảng \( (0;2) \).
Ta đã tìm được đạo hàm của hàm số:
\[ y' = \frac{x^2 - 2x - 1}{(x - 1)^2} \]
Để kiểm tra tính chất tăng giảm của hàm số trên khoảng \( (0;2) \), ta xét dấu của đạo hàm \( y' \) trên khoảng này.
- Khi \( x \in (0; 1 - \sqrt{2}) \cup (1 + \sqrt{2}; 2) \), đạo hàm \( y' < 0 \) (hàm số nghịch biến).
- Khi \( x \in (1 - \sqrt{2}; 1) \cup (1; 1 + \sqrt{2}) \), đạo hàm \( y' > 0 \) (hàm số đồng biến).
Do đó, hàm số không nghịch biến trên toàn bộ khoảng \( (0;2) \). Đáp án sai.
d) M là điểm bất kì thuộc đồ thị (C). Tích khoảng cách từ M đến tiệm cận đứng và tiệm cận xiên của đồ thị (C) bằng \( \sqrt{2} \).
Để tìm tiệm cận xiên, ta chia tử cho mẫu:
\[ y = \frac{x^2 + 2x - 1}{x - 1} = x + 3 + \frac{2}{x - 1} \]
Khi \( x \to \infty \), \( \frac{2}{x - 1} \to 0 \), vậy tiệm cận xiên là \( y = x + 3 \).
Gọi M có tọa độ \( (x_0, y_0) \). Khoảng cách từ M đến tiệm cận đứng \( x = 1 \) là \( |x_0 - 1| \).
Khoảng cách từ M đến tiệm cận xiên \( y = x + 3 \) là:
\[ \frac{|x_0 - y_0 + 3|}{\sqrt{1^2 + (-1)^2}} = \frac{|x_0 - (x_0 + 3 + \frac{2}{x_0 - 1}) + 3|}{\sqrt{2}} = \frac{|\frac{-2}{x_0 - 1}|}{\sqrt{2}} = \frac{2}{|x_0 - 1|\sqrt{2}} \]
Tích khoảng cách:
\[ |x_0 - 1| \cdot \frac{2}{|x_0 - 1|\sqrt{2}} = \frac{2}{\sqrt{2}} = \sqrt{2} \]
Vậy tích khoảng cách từ M đến tiệm cận đứng và tiệm cận xiên của đồ thị (C) bằng \( \sqrt{2} \). Đáp án đúng.
Kết luận
Đáp án đúng là:
a) Đúng
b) Đúng
c) Sai
d) Đúng
Câu 4.
Để giải quyết câu hỏi này, chúng ta sẽ thực hiện các bước sau:
1. Tìm vận tốc của chất điểm theo thời gian \( t \).
2. Kiểm tra các lựa chọn đã cho.
Bước 1: Tìm vận tốc của chất điểm theo thời gian \( t \).
Vận tốc \( v(t) \) của chất điểm là đạo hàm của phương trình chuyển động \( s(t) \):
\[ v(t) = \frac{ds}{dt} = \frac{d}{dt}(t^3 - 3t^2 + 8t + 1) = 3t^2 - 6t + 8 \]
Bước 2: Kiểm tra các lựa chọn đã cho.
a) Vận tốc của chất điểm tại thời điểm \( t = 3 \) (giây) bằng 8 m/s.
\[ v(3) = 3(3)^2 - 6(3) + 8 = 3 \cdot 9 - 18 + 8 = 27 - 18 + 8 = 17 \text{ m/s} \]
Vậy, lựa chọn a) sai.
b) Tại thời điểm mà chất điểm di chuyển được 13m, vận tốc khi đó bằng 8 m/s.
Phương trình chuyển động là \( s(t) = t^3 - 3t^2 + 8t + 1 \). Ta cần tìm \( t \) sao cho \( s(t) = 13 \):
\[ t^3 - 3t^2 + 8t + 1 = 13 \]
\[ t^3 - 3t^2 + 8t - 12 = 0 \]
Ta thử nghiệm các giá trị \( t \):
- Nếu \( t = 2 \):
\[ 2^3 - 3(2)^2 + 8(2) - 12 = 8 - 12 + 16 - 12 = 0 \]
Vậy \( t = 2 \) là nghiệm của phương trình. Bây giờ kiểm tra vận tốc tại \( t = 2 \):
\[ v(2) = 3(2)^2 - 6(2) + 8 = 3 \cdot 4 - 12 + 8 = 12 - 12 + 8 = 8 \text{ m/s} \]
Vậy, lựa chọn b) đúng.
c) Vận tốc nhỏ nhất của chất điểm là 5 m/s.
Để tìm vận tốc nhỏ nhất, ta cần tìm giá trị cực tiểu của hàm \( v(t) = 3t^2 - 6t + 8 \). Ta tính đạo hàm của \( v(t) \):
\[ v'(t) = \frac{d}{dt}(3t^2 - 6t + 8) = 6t - 6 \]
Đặt \( v'(t) = 0 \):
\[ 6t - 6 = 0 \]
\[ t = 1 \]
Kiểm tra giá trị của \( v(t) \) tại \( t = 1 \):
\[ v(1) = 3(1)^2 - 6(1) + 8 = 3 - 6 + 8 = 5 \text{ m/s} \]
Vậy, vận tốc nhỏ nhất của chất điểm là 5 m/s. Lựa chọn c) đúng.
d) Gia tốc tại thời điểm chất điểm đạt vận tốc nhỏ nhất bằng \( 2 \text{ m/s}^2 \).
Gia tốc \( a(t) \) là đạo hàm của vận tốc \( v(t) \):
\[ a(t) = \frac{dv}{dt} = \frac{d}{dt}(3t^2 - 6t + 8) = 6t - 6 \]
Tại thời điểm \( t = 1 \) (khi đạt vận tốc nhỏ nhất):
\[ a(1) = 6(1) - 6 = 0 \text{ m/s}^2 \]
Vậy, lựa chọn d) sai.
Kết luận: Các lựa chọn đúng là b) và c).
Đáp án: b) và c).
Câu 1.
Tổng số cách chọn 2 quả bóng từ 2 hộp là $10\times 12=120$ cách.
Số cách chọn 2 quả bóng có ít nhất 1 quả bóng ghi số 4 hoặc 6 là $(2+2)\times 12-(2+2)=48$ cách.
Suy ra Số cách chọn 2 quả bóng không có quả bóng nào ghi số 4 hoặc 6 là $120-48=72$ cách.
Vậy xác suất để hai quả bóng lấy được không có quả bóng nào ghi số 4 hoặc ghi số 6 là $\frac{72}{120}=\frac{3}{5}$.
Suy ra $a+b=3+5=8$.
Câu 2.
Đầu tiên, ta xác định tọa độ của con chim bói cá và con cá trong hệ tọa độ Oxyz.
Con chim bói cá cách mặt nước 2m, cách mặt phẳng (Oxz) là 3m và cách mặt phẳng (Oyz) là 1m. Do đó, tọa độ của con chim bói cá là \( (3; 1; 2) \).
Con cá cách mặt nước 50cm (tức là 0,5m), cách mặt phẳng (Oxz) là 1m và cách mặt phẳng (Oyz) là 1,5m. Do đó, tọa độ của con cá là \( (1; 1,5; 0,5) \).
Khi con chim bói cá phóng thẳng xuống vị trí con cá, nó sẽ đi qua điểm B, tức là điểm tiếp xúc với mặt nước. Mặt nước là mặt phẳng z = 0, do đó tọa độ của điểm B sẽ có dạng \( (a; b; 0) \).
Ta cần tìm tọa độ của điểm B. Ta thấy rằng đường thẳng từ con chim bói cá đến con cá sẽ có phương hướng từ \( (3; 1; 2) \) đến \( (1; 1,5; 0,5) \). Phương trình tham số của đường thẳng này là:
\[
\begin{cases}
x = 3 + t(1 - 3) \\
y = 1 + t(1,5 - 1) \\
z = 2 + t(0,5 - 2)
\end{cases}
\]
\[
\begin{cases}
x = 3 - 2t \\
y = 1 + 0,5t \\
z = 2 - 1,5t
\end{cases}
\]
Để tìm tọa độ của điểm B, ta đặt \( z = 0 \):
\[ 2 - 1,5t = 0 \]
\[ 1,5t = 2 \]
\[ t = \frac{2}{1,5} = \frac{4}{3} \]
Thay \( t = \frac{4}{3} \) vào phương trình tham số:
\[
\begin{cases}
x = 3 - 2 \left(\frac{4}{3}\right) = 3 - \frac{8}{3} = \frac{9}{3} - \frac{8}{3} = \frac{1}{3} \\
y = 1 + 0,5 \left(\frac{4}{3}\right) = 1 + \frac{2}{3} = \frac{3}{3} + \frac{2}{3} = \frac{5}{3} \\
z = 0
\end{cases}
\]
Do đó, tọa độ của điểm B là \( \left( \frac{1}{3}; \frac{5}{3}; 0 \right) \).
Bây giờ, ta tính \( T = 5a + 15b + 25c \):
\[ T = 5 \left( \frac{1}{3} \right) + 15 \left( \frac{5}{3} \right) + 25(0) \]
\[ T = \frac{5}{3} + \frac{75}{3} + 0 \]
\[ T = \frac{80}{3} \]
Vậy, \( T = \frac{80}{3} \).
Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh

 0
0



 0
0
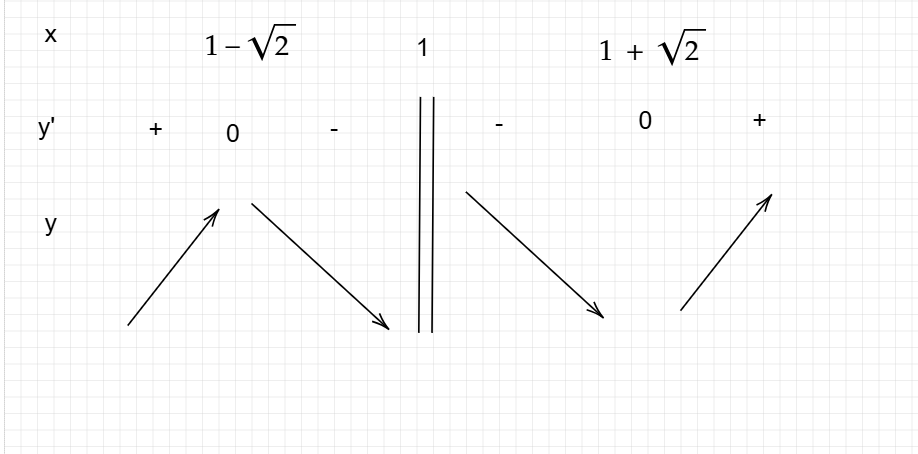
 0
0



