Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
24/12/2024
trả lời câu hỏi

 0
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



24/12/2024
 0
0
25/12/2024
Câu 3:
Giả sử vận tốc của máy bay theo hướng đông sang tây là , vận tốc của luồng gió theo hướng đông bắc sang tây nam là và vận tốc mới của máy bay chính là thỏa mãn . Ta cần tính độ dài vectơ .
Theo bài ra ta có: km/h, ∣ km/h,
.
Biểu diễn bài toán như hình vẽ dưới đây:
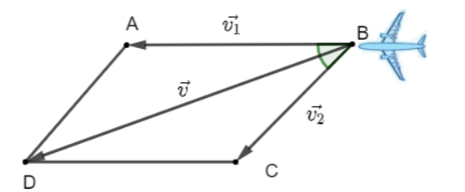
Khi đó ta có: ABCD là hình bình hành có .
Suy ra .
Ta cần tính độ dài đoạn thẳng BD, đây chính là độ dài vectơ →v .
Áp dụng định lí sin trong tam giác ABD, ta có:
BD2 = AD2 + AB2 – 2 . AD . AB . cosA
= 402 + 7002 – 2 . 40 . 700 . cos135°
≈ 531 197, 98
Suy ra BD ≈ 728,83 (km/h).
Vậy tốc độ mới của máy bay sau khi gặp gió thổi là 728,83 km/h.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
3 giờ trước
3 giờ trước
10 giờ trước
Top thành viên trả lời



