nhtbfggfnghfmg

CÂU 12: Để tính chiều dài đường cao \( BH \) trong tam giác vuông \( ABC \) với \( AB = 4,5 \, cm \) và \( BC = 6 \, cm \), ta thực hiện các bước sau: 1. Tính diện tích tam giác \( ABC \): Diện tích tam giác \( ABC \) được tính bằng công thức: \[ S_{ABC} = \frac{1}{2} \times AB \times BC = \frac{1}{2} \times 4,5 \times 6 = 13,5 \, cm^2 \] 2. Áp dụng công thức tính diện tích tam giác với đường cao: Diện tích tam giác \( ABC \) cũng có thể được tính bằng công thức: \[ S_{ABC} = \frac{1}{2} \times AC \times BH \] Trong đó, \( AC \) là cạnh huyền của tam giác \( ABC \). 3. Tính cạnh huyền \( AC \): Áp dụng định lý Pythagoras: \[ AC = \sqrt{AB^2 + BC^2} = \sqrt{4,5^2 + 6^2} = \sqrt{20,25 + 36} = \sqrt{56,25} = 7,5 \, cm \] 4. Tính đường cao \( BH \): Ta đã biết diện tích tam giác \( ABC \) là 13,5 cm² và cạnh huyền \( AC \) là 7,5 cm. Do đó: \[ 13,5 = \frac{1}{2} \times 7,5 \times BH \] Giải phương trình này để tìm \( BH \): \[ 13,5 = \frac{7,5}{2} \times BH \implies 13,5 = 3,75 \times BH \implies BH = \frac{13,5}{3,75} = 3,6 \, cm \] Vậy, đường cao \( BH \) bằng 3,6 cm. Đáp án đúng là C. 3,6 cm. Câu 13: Để phân thức $M=\frac{1}{x^2-2x}$ có nghĩa, mẫu số của phân thức phải khác 0. Ta có: \[ x^2 - 2x \neq 0 \] Phân tích mẫu số thành nhân tử: \[ x(x - 2) \neq 0 \] Điều này có nghĩa là: \[ x \neq 0 \quad \text{và} \quad x - 2 \neq 0 \] Từ đó ta có: \[ x \neq 0 \quad \text{và} \quad x \neq 2 \] Vậy điều kiện của x để phân thức có nghĩa là: \[ x \neq 2 \quad \text{và} \quad x \neq 0 \] Do đó, đáp án đúng là: D. $x \neq 2; x \neq 0$ Câu 14: Để tính độ dài BM trong tam giác ABC, ta sẽ sử dụng Định lý Cosin. Trước tiên, ta cần tìm góc BAC. Bước 1: Tính góc BAC bằng Định lý Cosin trong tam giác ABC: \[ \cos(\angle BAC) = \frac{AB^2 + AC^2 - BC^2}{2 \cdot AB \cdot AC} \] Thay các giá trị đã biết vào: \[ \cos(\angle BAC) = \frac{6^2 + 9^2 - 12^2}{2 \cdot 6 \cdot 9} = \frac{36 + 81 - 144}{108} = \frac{-27}{108} = -\frac{1}{4} \] Bước 2: Tính độ dài BM bằng Định lý Cosin trong tam giác ABM: \[ BM^2 = AB^2 + AM^2 - 2 \cdot AB \cdot AM \cdot \cos(\angle BAC) \] Thay các giá trị đã biết vào: \[ BM^2 = 6^2 + 4^2 - 2 \cdot 6 \cdot 4 \cdot \left(-\frac{1}{4}\right) \] \[ BM^2 = 36 + 16 + 12 = 64 \] Do đó: \[ BM = \sqrt{64} = 8 \text{ cm} \] Vậy độ dài BM là 8 cm. Đáp án đúng là: A. 8 cm. Câu 15: Để tìm giá trị của \( x \) sao cho \( N = 0 \), ta làm như sau: 1. Xác định điều kiện xác định (ĐKXĐ): Ta cần đảm bảo rằng mẫu số của phân thức không bằng 0. \[ x^2 - 4x + 4 \neq 0 \] Ta nhận thấy rằng: \[ x^2 - 4x + 4 = (x - 2)^2 \] Do đó: \[ (x - 2)^2 \neq 0 \implies x \neq 2 \] 2. Tìm giá trị của \( x \) sao cho \( N = 0 \): Để phân thức \( N \) bằng 0, tử số của phân thức phải bằng 0 (vì mẫu số không bằng 0): \[ x^2 - 4 = 0 \] Ta giải phương trình này: \[ x^2 - 4 = 0 \implies (x - 2)(x + 2) = 0 \] Từ đây, ta có hai trường hợp: \[ x - 2 = 0 \quad \text{hoặc} \quad x + 2 = 0 \] Giải các phương trình này: \[ x = 2 \quad \text{hoặc} \quad x = -2 \] 3. Kiểm tra điều kiện xác định: Ta đã xác định \( x \neq 2 \) để mẫu số không bằng 0. Do đó, giá trị \( x = 2 \) bị loại bỏ. Vậy, giá trị duy nhất còn lại là: \[ x = -2 \] Đáp án: C. \( x = -2 \) Bài 1: a) $\frac{2x+1}{3x+2}-\frac{x-3}{3x+2}$ - Để thực hiện phép trừ hai phân thức có cùng mẫu số, ta trừ hai tử số và giữ nguyên mẫu số: \[ \frac{2x+1}{3x+2} - \frac{x-3}{3x+2} = \frac{(2x+1)-(x-3)}{3x+2} = \frac{2x+1-x+3}{3x+2} = \frac{x+4}{3x+2} \] b) $\frac{5x-7}{x-4} + \frac{x+2}{x^2-16} : \frac{x+2}{4-x}$ - Trước tiên, ta nhận thấy rằng $x^2 - 16 = (x-4)(x+4)$ và $4-x = -(x-4)$. Do đó: \[ \frac{x+2}{x^2-16} : \frac{x+2}{4-x} = \frac{x+2}{(x-4)(x+4)} : \frac{x+2}{-(x-4)} = \frac{x+2}{(x-4)(x+4)} \times \frac{-(x-4)}{x+2} = \frac{-1}{x+4} \] - Tiếp theo, ta cộng hai phân thức: \[ \frac{5x-7}{x-4} + \frac{-1}{x+4} = \frac{(5x-7)(x+4) - (x-4)}{(x-4)(x+4)} = \frac{5x^2 + 20x - 7x - 28 - x + 4}{(x-4)(x+4)} = \frac{5x^2 + 12x - 24}{(x-4)(x+4)} \] c) $\frac{x-y}{x^2+2x} \cdot \frac{x^2-4}{x-y}$ - Ta nhận thấy rằng $x^2 + 2x = x(x+2)$ và $x^2 - 4 = (x-2)(x+2)$. Do đó: \[ \frac{x-y}{x(x+2)} \cdot \frac{(x-2)(x+2)}{x-y} = \frac{(x-y)(x-2)(x+2)}{x(x+2)(x-y)} = \frac{x-2}{x} \] d) $\frac{2x+10}{(x-3)^2} : \frac{x+5}{x^2-9}$ - Ta nhận thấy rằng $x^2 - 9 = (x-3)(x+3)$. Do đó: \[ \frac{2x+10}{(x-3)^2} : \frac{x+5}{(x-3)(x+3)} = \frac{2(x+5)}{(x-3)^2} \cdot \frac{(x-3)(x+3)}{x+5} = \frac{2(x+3)}{x-3} \] e) $\frac{x-3}{2x-1} - \frac{x-1}{2x+1}$ - Để thực hiện phép trừ hai phân thức, ta tìm mẫu số chung là $(2x-1)(2x+1)$: \[ \frac{x-3}{2x-1} - \frac{x-1}{2x+1} = \frac{(x-3)(2x+1) - (x-1)(2x-1)}{(2x-1)(2x+1)} = \frac{2x^2 + x - 6x - 3 - (2x^2 - x - 2x + 1)}{(2x-1)(2x+1)} = \frac{2x^2 - 5x - 3 - 2x^2 + 3x - 1}{(2x-1)(2x+1)} = \frac{-2x - 4}{(2x-1)(2x+1)} = \frac{-2(x+2)}{(2x-1)(2x+1)} \] Đáp số: a) $\frac{x+4}{3x+2}$ b) $\frac{5x^2 + 12x - 24}{(x-4)(x+4)}$ c) $\frac{x-2}{x}$ d) $\frac{2(x+3)}{x-3}$ e) $\frac{-2(x+2)}{(2x-1)(2x+1)}$ Bài 2: a) Điều kiện xác định của A: Phân thức $\frac{3x^2+6x}{x^2-4}$ có mẫu thức là $x^2 - 4$. Để phân thức này có nghĩa, mẫu thức phải khác 0. $x^2 - 4 \neq 0$ $(x - 2)(x + 2) \neq 0$ Do đó, $x \neq 2$ và $x \neq -2$. Vậy điều kiện xác định của A là $x \neq 2$ và $x \neq -2$. b) Rút gọn A: $\frac{3x^2+6x}{x^2-4} = \frac{3x(x+2)}{(x-2)(x+2)}$ = $\frac{3x}{x-2}$ (với điều kiện $x \neq -2$) c) Tính giá trị của A tại $x = -1$: Thay $x = -1$ vào biểu thức đã rút gọn: $A = \frac{3(-1)}{-1-2} = \frac{-3}{-3} = 1$ Vậy giá trị của A tại $x = -1$ là 1. d) Tìm giá trị lớn nhất của P biết $P = A : \frac{x^3-2x^2+3x}{x-2}$: $P = \frac{3x}{x-2} : \frac{x^3-2x^2+3x}{x-2}$ = $\frac{3x}{x-2} \times \frac{x-2}{x^3-2x^2+3x}$ = $\frac{3x}{x^3-2x^2+3x}$ = $\frac{3x}{x(x^2-2x+3)}$ = $\frac{3}{x^2-2x+3}$ Ta thấy rằng $x^2 - 2x + 3 = (x - 1)^2 + 2$, do đó $x^2 - 2x + 3$ luôn lớn hơn hoặc bằng 2 (vì $(x - 1)^2$ luôn lớn hơn hoặc bằng 0). Vậy $\frac{3}{x^2-2x+3}$ sẽ đạt giá trị lớn nhất khi mẫu số nhỏ nhất, tức là khi $x^2 - 2x + 3 = 2$. Giải phương trình $x^2 - 2x + 3 = 2$: $x^2 - 2x + 1 = 0$ $(x - 1)^2 = 0$ $x = 1$ Khi $x = 1$, giá trị của P là: $P = \frac{3}{1^2 - 2 \cdot 1 + 3} = \frac{3}{2}$ Vậy giá trị lớn nhất của P là $\frac{3}{2}$, đạt được khi $x = 1$. Bài 3: a) Ta có $\Delta DIK$ vuông tại D có đường cao DE. Xét $\Delta DIK$ và $\Delta EID$, ta có: - Cả hai tam giác đều có góc D chung. - Cả hai tam giác đều có góc vuông tại I và E lần lượt. Do đó, theo tiêu chí góc-góc, ta có $\Delta DIK \sim \Delta EID$. b) Áp dụng định lý Pythagoras trong tam giác vuông DIK, ta có: \[ IK^2 = DI^2 + DK^2 \] \[ IK^2 = 9^2 + 12^2 \] \[ IK^2 = 81 + 144 \] \[ IK^2 = 225 \] \[ IK = \sqrt{225} \] \[ IK = 15 \text{ cm} \] Áp dụng tính chất của tam giác vuông có đường cao hạ từ đỉnh góc vuông, ta có: \[ DE = \frac{DI \times DK}{IK} \] \[ DE = \frac{9 \times 12}{15} \] \[ DE = \frac{108}{15} \] \[ DE = 7.2 \text{ cm} \] Áp dụng tính chất của tam giác vuông có đường cao hạ từ đỉnh góc vuông, ta có: \[ EK = \frac{DK^2}{IK} \] \[ EK = \frac{12^2}{15} \] \[ EK = \frac{144}{15} \] \[ EK = 9.6 \text{ cm} \] Đáp số: - IK = 15 cm - DE = 7.2 cm - EK = 9.6 cm Bài 4: Để chứng minh đẳng thức $\frac{x+1}{x-2}-\frac{2x-1}{x^2-4}-\frac x{x+2}=\frac{3x+3}{x^2-4}$, ta thực hiện các bước sau: Bước 1: Xác định điều kiện xác định (ĐKXĐ): - Các phân thức có mẫu số là $x-2$, $x^2-4$, và $x+2$. Ta cần đảm bảo các mẫu số này khác 0. - Điều kiện xác định là: $x \neq 2$, $x \neq -2$. Bước 2: Quy đồng mẫu số các phân thức: - Mẫu số chung của các phân thức là $(x-2)(x+2)$. - Ta có: \[ \frac{x+1}{x-2} = \frac{(x+1)(x+2)}{(x-2)(x+2)} \] \[ \frac{2x-1}{x^2-4} = \frac{2x-1}{(x-2)(x+2)} \] \[ \frac{x}{x+2} = \frac{x(x-2)}{(x+2)(x-2)} \] Bước 3: Thực hiện phép trừ các phân thức: - Ta có: \[ \frac{(x+1)(x+2)}{(x-2)(x+2)} - \frac{2x-1}{(x-2)(x+2)} - \frac{x(x-2)}{(x+2)(x-2)} \] - Kết hợp các phân thức lại: \[ \frac{(x+1)(x+2) - (2x-1) - x(x-2)}{(x-2)(x+2)} \] Bước 4: Rút gọn tử số: - Ta có: \[ (x+1)(x+2) = x^2 + 3x + 2 \] \[ -(2x-1) = -2x + 1 \] \[ -x(x-2) = -x^2 + 2x \] - Cộng các biểu thức trên: \[ x^2 + 3x + 2 - 2x + 1 - x^2 + 2x = 3x + 3 \] Bước 5: Viết kết quả cuối cùng: - Ta có: \[ \frac{3x + 3}{(x-2)(x+2)} = \frac{3x + 3}{x^2 - 4} \] Vậy, ta đã chứng minh được đẳng thức $\frac{x+1}{x-2}-\frac{2x-1}{x^2-4}-\frac x{x+2}=\frac{3x+3}{x^2-4}$. Bài 5: a) Ta có: $\Delta AHD$ vuông tại $H$ và $\Delta CKD$ vuông tại $K$. Ta thấy $\Delta AHD$ và $\Delta CKD$ có: - $AD = BC$ (tính chất hình bình hành) - $\angle ADH = \angle BCK$ (hai góc so le trong) - $\angle AHD = \angle CKB = 90^\circ$ (vì $AH \perp CD$ và $CK \perp AB$) Do đó, theo trường hợp bằng nhau thứ 2 (cạnh kề 2 góc vuông), ta có $\Delta AHD = \Delta CKD$. Từ đó suy ra $AH = CK$ và $DH = BK$. b) Ta có $AH \perp CD$ và $CK \perp AB$, nên $AH$ và $CK$ là các đường cao hạ từ đỉnh $A$ và $C$ xuống đáy $CD$ và $AB$ tương ứng. Xét tam giác $AIH$ và tam giác $DIK$, ta thấy: - $\angle AIH = \angle DIK$ (góc chung) - $\angle AHI = \angle DKA = 90^\circ$ (vì $AH \perp CD$ và $CK \perp AB$) Do đó, theo trường hợp bằng nhau thứ 1 (góc - cạnh - góc), ta có $\Delta AIH \sim \Delta DIK$. Từ đó suy ra tỉ lệ thức: $\frac{IA}{ID} = \frac{IH}{IK}$. Nhân cả 2 vế với $ID \times IK$, ta được: $IA \times ID = IH \times IK$. Đáp số: $IA \times ID = IH \times IK$. Bài 6: Ta có: $x + y + z = 0$ (1) Bước 1: Bình phương cả hai vế của (1): $(x + y + z)^2 = 0^2$ $x^2 + y^2 + z^2 + 2xy + 2yz + 2zx = 0$ Bước 2: Sắp xếp lại phương trình: $x^2 + y^2 + z^2 = -2(xy + yz + zx)$ Bước 3: Xét mẫu số của biểu thức $A$: $(x - y)^2 + (y - z)^2 + (z - x)^2$ Bước 4: Mở rộng các bình phương: $(x - y)^2 = x^2 - 2xy + y^2$ $(y - z)^2 = y^2 - 2yz + z^2$ $(z - x)^2 = z^2 - 2zx + x^2$ Bước 5: Cộng các biểu thức trên: $(x - y)^2 + (y - z)^2 + (z - x)^2 = x^2 - 2xy + y^2 + y^2 - 2yz + z^2 + z^2 - 2zx + x^2$ $= 2(x^2 + y^2 + z^2) - 2(xy + yz + zx)$ Bước 6: Thay $x^2 + y^2 + z^2 = -2(xy + yz + zx)$ vào mẫu số: $2(x^2 + y^2 + z^2) - 2(xy + yz + zx) = 2(-2(xy + yz + zx)) - 2(xy + yz + zx)$ $= -4(xy + yz + zx) - 2(xy + yz + zx)$ $= -6(xy + yz + zx)$ Bước 7: Thay vào biểu thức $A$: $A = \frac{x^2 + y^2 + z^2}{(x - y)^2 + (y - z)^2 + (z - x)^2}$ $= \frac{-2(xy + yz + zx)}{-6(xy + yz + zx)}$ $= \frac{1}{3}$ Vậy $A = \frac{1}{3}$. 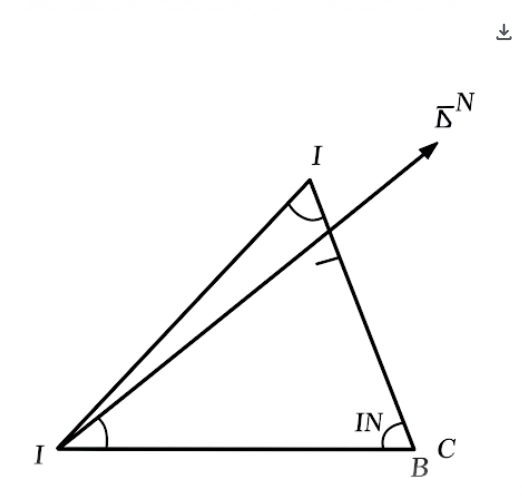Bài 7: a) Ta có $\Delta BNI$ và $\Delta BAC$ có: - $\widehat{B}$ chung - $\widehat{BNI} = \widehat{BAC} = 90^\circ$ Do đó, $\Delta BNI \sim \Delta BAC$ (góc - góc) b) Biết $AB = 8$ cm, $BC = 10$ cm. Ta cần tính $BN$. Vì $I$ là trung điểm của $AB$, nên $BI = \frac{AB}{2} = \frac{8}{2} = 4$ cm. Ta có $\Delta BNI \sim \Delta BAC$, nên ta có tỉ lệ: \[ \frac{BN}{BA} = \frac{BI}{BC} \] Thay các giá trị đã biết vào: \[ \frac{BN}{8} = \frac{4}{10} = \frac{2}{5} \] Từ đó, ta có: \[ BN = 8 \times \frac{2}{5} = \frac{16}{5} = 3.2 \text{ cm} \] c) Để chứng minh $I\widehat{AN} = \widehat{CAN}$, ta sẽ sử dụng kết quả từ câu a. Ta đã chứng minh $\Delta BNI \sim \Delta BAC$. Do đó, ta có: \[ \frac{BN}{BA} = \frac{BI}{BC} \] Từ đây, ta có: \[ BN \cdot BC = BI \cdot BA \] Ta cũng có $\Delta BAN \sim \Delta BCI$ (cạnh - góc - cạnh), do đó: \[ \widehat{BAN} = \widehat{BCI} \] Vì $\widehat{BAN} = \widehat{BCI}$, nên ta có: \[ I\widehat{AN} = \widehat{CAN} \] Đáp số: a) $\Delta BNI \sim \Delta BAC$ b) $BN = 3.2$ cm c) $I\widehat{AN} = \widehat{CAN}$