hình như mình sai câu 2 tự luận đg k ạ

Câu 1. Để giải quyết câu hỏi này, chúng ta sẽ kiểm tra từng phát biểu một. a) Tỉ lệ phần trăm của chất khoáng là 35%. - Từ biểu đồ hình quạt tròn, ta thấy rằng chất khoáng chiếm 35%. - Phát biểu này đúng. b) Thành phần chiếm tỉ lệ cao nhất là nước. - Từ biểu đồ, ta thấy rằng nước chiếm 40%, là tỉ lệ phần trăm cao nhất. - Phát biểu này đúng. c) Tỉ số thành phần của chất mùn so với thành phần không khí là $\frac{1}{5}$. - Chất mùn chiếm 10% và không khí chiếm 50%. - Tỉ số của chất mùn so với không khí là $\frac{10\%}{50\%} = \frac{1}{5}$. - Phát biểu này đúng. d) Muốn thu 125 kg mùn thì cần 2500 kg đất. - Chất mùn chiếm 10% trong tổng lượng đất. - Để thu được 125 kg mùn, ta cần tính tổng lượng đất cần thiết. - Ta có: 10% của tổng lượng đất = 125 kg. - Tổng lượng đất cần thiết = $\frac{125}{10\%} = \frac{125}{0,1} = 1250$ kg. - Phát biểu này sai vì cần 1250 kg đất, không phải 2500 kg. Kết luận: - Phát biểu a) đúng. - Phát biểu b) đúng. - Phát biểu c) đúng. - Phát biểu d) sai. Đáp án: a) Đúng, b) Đúng, c) Đúng, d) Sai. Câu 2. a) Số đo góc C là $70^0$ - Ta biết tổng ba góc trong một tam giác bằng $180^0$. - Số đo góc C là: $180^0 - (\widehat{A} + \widehat{B}) = 180^0 - (70^0 + 50^0) = 60^0$. - Vậy số đo góc C là $60^0$, không phải $70^0$. b) Cạnh đối diện với góc C là AB . AC - Cạnh đối diện với góc C là cạnh AB. c) Cạnh lớn nhất là BC, cạnh nhỏ nhất là - Trong tam giác, cạnh đối diện với góc lớn nhất sẽ là cạnh lớn nhất. Vì $\widehat{A} = 70^0$ là góc lớn nhất, nên cạnh BC là cạnh lớn nhất. - Cạnh nhỏ nhất là cạnh đối diện với góc nhỏ nhất. Vì $\widehat{C} = 60^0$ là góc nhỏ nhất, nên cạnh nhỏ nhất là cạnh AB. d) Giả sử $AC=2~cm,~AB=5~cm.$ Độ dài cạnh BC là 8cm. - Theo bất đẳng thức tam giác, tổng độ dài hai cạnh bất kỳ phải lớn hơn độ dài cạnh còn lại. - Ta kiểm tra: $AC + AB = 2~cm + 5~cm = 7~cm < 8~cm$ (không thỏa mãn bất đẳng thức tam giác). - Do đó, độ dài cạnh BC không thể là 8 cm. Đáp số: a) Số đo góc C là $60^0$. b) Cạnh đối diện với góc C là AB. c) Cạnh lớn nhất là BC, cạnh nhỏ nhất là AB. d) Độ dài cạnh BC không thể là 8 cm. Câu 1. a) Dân số Việt Nam năm 2019 là 97 triệu người. b) Dân số Việt Nam năm 1999 là 77 triệu người. Dân số Việt Nam năm 2009 tăng số phần trăm so với năm 1999 là (87 – 77) x 100 : 77 = 12,987% Đáp số: a) 97 triệu người b) 12,987% Câu 2 a) Tập hợp A gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là: \[ A = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\} \] b) Biến cố "Số xuất hiện trên thẻ là số chẵn" bao gồm các số: 2, 4, 6, 8, 10, 12. Tập hợp các kết quả có thể xảy ra của biến cố này là: \[ B = \{2, 4, 6, 8, 10, 12\} \] Số lượng các kết quả có thể xảy ra của biến cố này là 6. Xác suất của biến cố "Số xuất hiện trên thẻ là số chẵn" là: \[ P(B) = \frac{\text{số lượng các kết quả có thể xảy ra của biến cố}}{\text{số lượng các kết quả có thể xảy ra của toàn bộ biến cố}} = \frac{6}{12} = \frac{1}{2} \] c) Biến cố "Số xuất hiện trên thẻ là số nguyên tố" bao gồm các số: 2, 3, 5, 7, 11. Tập hợp các kết quả có thể xảy ra của biến cố này là: \[ C = \{2, 3, 5, 7, 11\} \] Số lượng các kết quả có thể xảy ra của biến cố này là 5. Xác suất của biến cố "Số xuất hiện trên thẻ là số nguyên tố" là: \[ P(C) = \frac{\text{số lượng các kết quả có thể xảy ra của biến cố}}{\text{số lượng các kết quả có thể xảy ra của toàn bộ biến cố}} = \frac{5}{12} \] Đáp số: a) \( A = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\} \) b) \( P(B) = \frac{1}{2} \) c) \( P(C) = \frac{5}{12} \) Câu 3. Để tính giá trị của biểu thức \( M = 3xz^2 - 2y \) tại \( x = 2 \), \( y = -1 \), \( z = -3 \): Bước 1: Thay giá trị của \( x \), \( y \), và \( z \) vào biểu thức \( M \): \[ M = 3 \cdot 2 \cdot (-3)^2 - 2 \cdot (-1) \] Bước 2: Tính giá trị của \( (-3)^2 \): \[ (-3)^2 = 9 \] Bước 3: Thay giá trị này vào biểu thức: \[ M = 3 \cdot 2 \cdot 9 - 2 \cdot (-1) \] Bước 4: Thực hiện phép nhân: \[ 3 \cdot 2 = 6 \] \[ 6 \cdot 9 = 54 \] \[ 2 \cdot (-1) = -2 \] Bước 5: Thay kết quả của các phép nhân vào biểu thức: \[ M = 54 - (-2) \] Bước 6: Thực hiện phép trừ: \[ 54 - (-2) = 54 + 2 = 56 \] Vậy giá trị của biểu thức \( M \) tại \( x = 2 \), \( y = -1 \), \( z = -3 \) là 56. 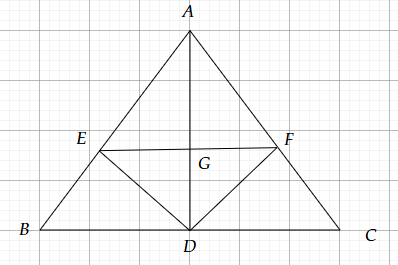Câu 4. a) Ta có: - \(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\)) - \(AD\) là tia phân giác của góc \(A\), nên \(\angle BAD = \angle CAD\) - \(AD\) chung Do đó, theo trường hợp bằng nhau thứ hai (cạnh kề hai góc bằng nhau), ta có: \[ \Delta ABD = \Delta ACD \] b) Vì \(\Delta ABD = \Delta ACD\), nên các cạnh tương ứng bằng nhau: - \(BD = CD\) - \(DE \perp AB\) và \(DF \perp AC\) Do đó, \(DE\) và \(DF\) là các đường cao hạ từ \(D\) xuống \(AB\) và \(AC\) tương ứng. Vì \(\Delta ABD = \Delta ACD\), nên các đường cao hạ từ đỉnh \(D\) xuống các cạnh \(AB\) và \(AC\) sẽ bằng nhau: \[ DE = DF \] c) Ta có: - \(DE \perp AB\) và \(DF \perp AC\) - \(DE = DF\) (chứng minh ở phần b) Gọi \(G\) là giao điểm của \(AD\) và \(EF\). Ta cần chứng minh \(EF // BC\). Xét tam giác \(ADE\) và tam giác \(ADF\): - \(DE = DF\) (chứng minh ở phần b) - \(AD\) chung - \(\angle ADE = \angle ADF = 90^\circ\) (vì \(DE \perp AB\) và \(DF \perp AC\)) Do đó, theo trường hợp bằng nhau thứ ba (cạnh huyền và một cạnh góc vuông), ta có: \[ \Delta ADE = \Delta ADF \] Vì \(\Delta ADE = \Delta ADF\), nên các góc tương ứng bằng nhau: - \(\angle AED = \angle AFD\) Mặt khác, \(AD\) là tia phân giác của góc \(A\), nên: - \(\angle BAD = \angle CAD\) Do đó, ta có: - \(\angle EAD = \angle FAD\) Vì \(\angle EAD = \angle FAD\) và \(\angle AED = \angle AFD\), nên \(EF\) song song với \(BC\) (theo dấu hiệu nhận biết hai đường thẳng song song). Vậy ta đã chứng minh được \(EF // BC\). Đáp số: \(EF // BC\) - HẾT - Chúc các em tự tin và làm bài tốt.