Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
rdrdrdrdrd4s4s4srs

 0
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



19/03/2025
 0
0
19/03/2025
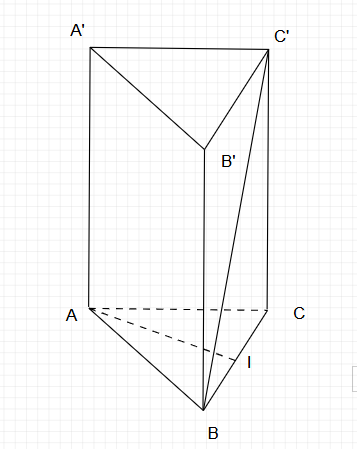
Tam giác ABC đều có I là trung điểm của BC
⟹ AI là trung tuyến đồng thời là đường cao
⟹ $\displaystyle AI\bot BC\equiv I$ (1)
Lăng trụ ABC.A'B'C' có $\displaystyle A'A\bot ( ABC)$
⟹ $\displaystyle C'C\bot ( ABC) \equiv C$
⟹ $\displaystyle C'C\bot AI$ (2)
Từ (1); (2) ⟹ $\displaystyle AI\bot ( BCC'B')$
Có $\displaystyle BC'\subset ( BCC'B')$
⟹ $\displaystyle AI\bot BC'$
⟹ $\displaystyle ( AI,BC') =90^{0}$
 0
0
19/03/2025
Huệ Mỹ Vậy ta hãy phân tích bài toán về hình lăng trụ tam giác đều \( ABC \cdot A'B'C' \) với các chi tiết sau:
**Bài toán tóm tắt:**
1. Đáy \( ABC \) là một tam giác đều cạnh \( a \).
2. \( A'A \) vuông góc với mặt phẳng \( (ABC) \) và \( A'A = 2a \).
3. \( I \) là trung điểm của cạnh \( BC \).
4. Yêu cầu tính góc giữa hai đường thẳng \( AI \) và \( BC \).
**Giải bài toán:**
Để tính góc giữa hai đường thẳng, ta sử dụng công thức:
\[
\cos \theta = \frac{\vec{u} \cdot \vec{v}}{\|\vec{u}\| \cdot \|\vec{v}\|}
\]
Với:
- \(\vec{u} = \overrightarrow{AI}\) (đường thẳng từ \( A \) đến \( I \)).
- \(\vec{v} = \overrightarrow{BC}\) (đường thẳng cạnh đáy).
1. **Tọa độ điểm và vector:**
- Đặt \( A(0, 0, 0) \), \( B(a, 0, 0) \), \( C\left(\frac{a}{2}, \frac{a\sqrt{3}}{2}, 0\right) \).
- Trung điểm \( I \left(\frac{3a}{4}, \frac{a\sqrt{3}}{4}, 0\right) \).
- Điểm \( A'(0, 0, 2a) \).
2. **Vector \(\overrightarrow{AI}\):**
\[
\overrightarrow{AI} = \left(\frac{3a}{4}, \frac{a\sqrt{3}}{4}, 2a\right)
\]
3. **Vector \(\overrightarrow{BC}\):**
\[
\overrightarrow{BC} = \left(-\frac{a}{2}, \frac{a\sqrt{3}}{2}, 0\right)
\]
4. **Tích vô hướng:**
\[
\vec{u} \cdot \vec{v} = \frac{3a}{4} \cdot \left(-\frac{a}{2}\right) + \frac{a\sqrt{3}}{4} \cdot \frac{a\sqrt{3}}{2} + 2a \cdot 0
\]
5. **Độ lớn vector:**
Tính \(\|\vec{u}\|\) và \(\|\vec{v}\|\).
Dựa vào các bước này, bạn có thể tự tính toán hoặc mình tiếp tục giải chi tiết từng phần nhé! 😊
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
06/12/2025
Top thành viên trả lời



