Giúp mình với!

Câu 1 1. Thực hiện các phép tính sau: \[ A = 1\frac{13}{15} \cdot (0,5)^2 \cdot 3 + \left(\frac{8}{15} - 1\frac{19}{60}\right) : 1\frac{23}{24} \] \[ B = \left(\frac{1}{2^2} - 1\right) \cdot \left(\frac{1}{3^2} - 1\right) \cdot \left(\frac{1}{4^2} - 1\right) \cdots \left(\frac{1}{2025^2} - 1\right) \] Phép tính A: \[ 1\frac{13}{15} = \frac{28}{15} \] \[ (0,5)^2 = 0,25 = \frac{1}{4} \] \[ \frac{8}{15} - 1\frac{19}{60} = \frac{8}{15} - \frac{79}{60} = \frac{32}{60} - \frac{79}{60} = -\frac{47}{60} \] \[ 1\frac{23}{24} = \frac{47}{24} \] Do đó: \[ A = \frac{28}{15} \cdot \frac{1}{4} \cdot 3 + \left(-\frac{47}{60}\right) : \frac{47}{24} \] \[ = \frac{28}{15} \cdot \frac{3}{4} + \left(-\frac{47}{60}\right) \cdot \frac{24}{47} \] \[ = \frac{28 \cdot 3}{15 \cdot 4} + \left(-\frac{47 \cdot 24}{60 \cdot 47}\right) \] \[ = \frac{84}{60} + \left(-\frac{24}{60}\right) \] \[ = \frac{84 - 24}{60} \] \[ = \frac{60}{60} \] \[ = 1 \] Phép tính B: \[ \frac{1}{n^2} - 1 = \frac{1 - n^2}{n^2} = \frac{(1-n)(1+n)}{n^2} \] Do đó: \[ B = \left(\frac{(1-2)(1+2)}{2^2}\right) \cdot \left(\frac{(1-3)(1+3)}{3^2}\right) \cdots \left(\frac{(1-2025)(1+2025)}{2025^2}\right) \] \[ = \left(\frac{-1 \cdot 3}{2^2}\right) \cdot \left(\frac{-2 \cdot 4}{3^2}\right) \cdots \left(\frac{-2024 \cdot 2026}{2025^2}\right) \] Nhận thấy các phân số liên tiếp sẽ triệt tiêu dần: \[ B = \frac{-1 \cdot 2026}{2 \cdot 2025} = \frac{-2026}{4050} = -\frac{1013}{2025} \] 2. Cho \(\frac{x+2024}{x-2024} = \frac{y+2025}{y-2025}\) (với \(x \neq 2024\) và \(y \neq 2025\)). Chứng minh rằng \(\frac{x}{y} = \frac{2024}{2025}\). Chứng minh: \[ \frac{x+2024}{x-2024} = \frac{y+2025}{y-2025} \] Nhân cả hai vế với \((x-2024)\) và \((y-2025)\): \[ (x+2024)(y-2025) = (x-2024)(y+2025) \] Mở ngoặc: \[ xy - 2025x + 2024y - 2024 \cdot 2025 = xy + 2025x - 2024y - 2024 \cdot 2025 \] Cộng trừ các hạng tử: \[ -2025x + 2024y = 2025x - 2024y \] Di chuyển các hạng tử: \[ 2024y + 2024y = 2025x + 2025x \] \[ 4048y = 4050x \] Chia cả hai vế cho 4048: \[ y = \frac{4050}{4048}x \] \[ y = \frac{2025}{2024}x \] Do đó: \[ \frac{x}{y} = \frac{2024}{2025} \] Đáp số: \[ A = 1 \] \[ B = -\frac{1013}{2025} \] \[ \frac{x}{y} = \frac{2024}{2025} \] Câu 2 1. Ta có: \[ \frac{x-1}{2} = \frac{y-2}{3} = \frac{z-3}{4} \] Gọi $\frac{x-1}{2} = \frac{y-2}{3} = \frac{z-3}{4} = k$ Suy ra: \[ x = 2k + 1, \quad y = 3k + 2, \quad z = 4k + 3 \] Thay vào phương trình $x - 2y + 3z = 14$, ta có: \[ (2k + 1) - 2(3k + 2) + 3(4k + 3) = 14 \] \[ 2k + 1 - 6k - 4 + 12k + 9 = 14 \] \[ 8k + 6 = 14 \] \[ 8k = 8 \] \[ k = 1 \] Vậy: \[ x = 2 \cdot 1 + 1 = 3 \] \[ y = 3 \cdot 1 + 2 = 5 \] \[ z = 4 \cdot 1 + 3 = 7 \] Đáp số: $x = 3, y = 5, z = 7$ 2. Gọi số tấn hàng theo kế hoạch ban đầu đội I, đội II và đội III được giao lần lượt là $a$, $b$, $c$ (tấn). Theo đề bài, ta có: \[ a + b + c = 3030 \] Thực tế, đội I vận chuyển được: \[ a + 0.26a = 1.26a \] Đội II vận chuyển được: \[ b + 0.05b = 1.05b \] Đội III vận chuyển được: \[ c + 0.08c = 1.08c \] Theo đề bài, khối lượng hàng mà ba đội đã vận chuyển được là bằng nhau, tức là: \[ 1.26a = 1.05b = 1.08c \] Gọi $1.26a = 1.05b = 1.08c = k$. Suy ra: \[ a = \frac{k}{1.26}, \quad b = \frac{k}{1.05}, \quad c = \frac{k}{1.08} \] Thay vào phương trình $a + b + c = 3030$, ta có: \[ \frac{k}{1.26} + \frac{k}{1.05} + \frac{k}{1.08} = 3030 \] Tìm chung mẫu số: \[ \frac{k}{1.26} = \frac{100k}{126}, \quad \frac{k}{1.05} = \frac{100k}{105}, \quad \frac{k}{1.08} = \frac{100k}{108} \] Chuyển về cùng mẫu số: \[ \frac{100k}{126} + \frac{100k}{105} + \frac{100k}{108} = 3030 \] Chuyển về cùng mẫu số chung là 1260: \[ \frac{1000k}{1260} + \frac{1200k}{1260} + \frac{1166.67k}{1260} = 3030 \] Cộng các phân số: \[ \frac{3366.67k}{1260} = 3030 \] Nhân cả hai vế với 1260: \[ 3366.67k = 3030 \times 1260 \] \[ 3366.67k = 3817800 \] \[ k = \frac{3817800}{3366.67} \approx 1134 \] Vậy: \[ a = \frac{1134}{1.26} = 900 \] \[ b = \frac{1134}{1.05} = 1080 \] \[ c = \frac{1134}{1.08} = 1050 \] Đáp số: Đội I: 900 tấn, Đội II: 1080 tấn, Đội III: 1050 tấn. Câu 3 1. Ta có: \[ A = \frac{x+1}{x-3} = \frac{(x-3)+4}{x-3} = 1 + \frac{4}{x-3} \] Để A có giá trị lớn nhất, ta cần $\frac{4}{x-3}$ có giá trị lớn nhất. Điều này xảy ra khi $|x-3|$ nhỏ nhất và $x-3$ khác 0. Do đó, giá trị nhỏ nhất của $|x-3|$ là 1 (khi $x = 4$ hoặc $x = 2$). - Khi $x = 4$, ta có: \[ A = 1 + \frac{4}{4-3} = 1 + 4 = 5 \] - Khi $x = 2$, ta có: \[ A = 1 + \frac{4}{2-3} = 1 - 4 = -3 \] Giá trị lớn nhất của A là 5, đạt được khi $x = 4$. 2. Ta có: \[ 3xy - 5x - 6y + 7 = 0 \] \[ 3xy - 5x - 6y + 10 = 3 \] \[ 3x(y - 2) - 6(y - 2) = 3 \] \[ (3x - 6)(y - 2) = 3 \] Ta xét các trường hợp: - $(3x - 6) = 1$ và $(y - 2) = 3$ \[ 3x - 6 = 1 \Rightarrow 3x = 7 \Rightarrow x = \frac{7}{3} \] (loại vì x phải là số nguyên) \[ y - 2 = 3 \Rightarrow y = 5 \] - $(3x - 6) = 3$ và $(y - 2) = 1$ \[ 3x - 6 = 3 \Rightarrow 3x = 9 \Rightarrow x = 3 \] \[ y - 2 = 1 \Rightarrow y = 3 \] - $(3x - 6) = -1$ và $(y - 2) = -3$ \[ 3x - 6 = -1 \Rightarrow 3x = 5 \Rightarrow x = \frac{5}{3} \] (loại vì x phải là số nguyên) \[ y - 2 = -3 \Rightarrow y = -1 \] - $(3x - 6) = -3$ và $(y - 2) = -1$ \[ 3x - 6 = -3 \Rightarrow 3x = 3 \Rightarrow x = 1 \] \[ y - 2 = -1 \Rightarrow y = 1 \] Vậy các cặp số nguyên (x, y) thỏa mãn là: (3, 3), (1, 1). 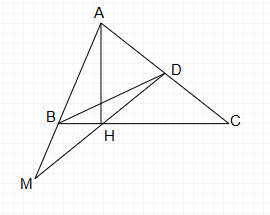Câu 4 a) Xét tam giác BHM có BM = BH nên tam giác BHM là tam giác cân tại B. $\widehat{AMH}=\widehat{MBH}+\widehat{BHM}=\widehat{MBH}+\widehat{BMH}=\widehat{AHB}=\widehat{ACB}.$ b) Ta có $\widehat{MHD}=\widehat{ACD}+\widehat{CAD}.$ Mà $\widehat{MHD}=\widehat{MBH}+\widehat{BMH}=\widehat{MBH}+\widehat{BHM}=\widehat{AHB}=\widehat{ACB}.$ Suy ra $\widehat{ACD}+\widehat{CAD}=\widehat{ACB}.$ Từ đó suy ra $\widehat{CAD}=\widehat{BAD}.$ Xét tam giác ACD và BAD có: $\widehat{CAD}=\widehat{BAD};$ AD là cạnh chung; $\widehat{ADC}=\widehat{ADB}=90^{\circ }.$ Suy ra tam giác ACD và BAD bằng nhau (g.c.gn). Suy ra CD = BD. c) Từ kết quả trên ta có AC = AB. Xét tam giác AHC và AMB có: AC = AB; $\widehat{ACH}=\widehat{AMB};$ HC = MB. Suy ra tam giác AHC và AMB bằng nhau (cạnh kề 2 góc). Suy ra AM = HC. d) Ta có $\widehat{ABD}=\widehat{ACB}+\widehat{CBD}.$ Mà $\widehat{ABC}=2\widehat{ACB}.$ Suy ra $\widehat{ABD}=\widehat{ACB}+\widehat{CBD}=\widehat{ACB}+\widehat{CBH}=\widehat{ABC}=\widehat{ACB}+\widehat{ACB}.$ Từ đó suy ra $\widehat{CBD}=\widehat{ACB}.$ Suy ra $\widehat{CBD}=\widehat{CDB}.$ Suy ra tam giác CBD là tam giác cân tại C. Suy ra BD = CD. Ta có $BD=\frac{CD+AD}{2}=\frac{AC}{2}.$ Mà AC < AB + BC. Suy ra $BD< \frac{AB+BC}{2}.$ Câu 5 Để tìm các số nguyên tố \( x \) và \( y \) thỏa mãn phương trình \( x^2 - 6y^2 = 1 \), chúng ta sẽ thực hiện các bước sau: 1. Kiểm tra các trường hợp nhỏ: - Đầu tiên, chúng ta thử các giá trị nhỏ của \( y \) để xem liệu có thể tìm được \( x \) là số nguyên tố hay không. 2. Thử \( y = 1 \): \[ x^2 - 6 \cdot 1^2 = 1 \implies x^2 - 6 = 1 \implies x^2 = 7 \implies x = \sqrt{7} \] \( x = \sqrt{7} \) không phải là số nguyên, do đó không thỏa mãn. 3. Thử \( y = 2 \): \[ x^2 - 6 \cdot 2^2 = 1 \implies x^2 - 24 = 1 \implies x^2 = 25 \implies x = 5 \] \( x = 5 \) là số nguyên tố, do đó \( (x, y) = (5, 2) \) là một nghiệm. 4. Kiểm tra các giá trị lớn hơn của \( y \): - Chúng ta cần kiểm tra xem liệu có các giá trị khác của \( y \) lớn hơn 2 có thể thỏa mãn phương trình hay không. - Tuy nhiên, khi \( y \) lớn hơn 2, \( 6y^2 \) sẽ lớn hơn 24, và \( x^2 \) sẽ phải lớn hơn 25. Điều này làm tăng khả năng \( x \) không phải là số nguyên tố hoặc không thỏa mãn phương trình. 5. Kết luận: - Từ các phép tính trên, chúng ta thấy rằng \( (x, y) = (5, 2) \) là nghiệm duy nhất thỏa mãn phương trình \( x^2 - 6y^2 = 1 \) với \( x \) và \( y \) là số nguyên tố. Do đó, các số nguyên tố \( x \) và \( y \) thỏa mãn phương trình \( x^2 - 6y^2 = 1 \) là: \[ (x, y) = (5, 2) \]