giúp mình với

Câu 1. Mặt phẳng $(\alpha)$ đi qua điểm $M(5;4;3)$ và cắt các tia Ox, Oy, Oz các đoạn bằng nhau. Suy ra $(\alpha)$ đi qua 3 điểm $A(a;0;0), B(0;a;0), C(0;0;a)$ Phương trình mặt phang $(\alpha)$ đi qua 3 điểm $A, B, C$ là: $\frac{x}{a} + \frac{y}{a} + \frac{z}{a} = 1$ Hay $x + y + z - a = 0$ Mặt phẳng $(\alpha)$ đi qua điểm $M(5;4;3)$ Suy ra $5 + 4 + 3 - a = 0$ Vậy $a = 12$ Phương trình mặt phẳng $(\alpha)$ là $x + y + z - 12 = 0$ Vậy $c = -12$ Câu 2. Để giải bài toán này, chúng ta sẽ thực hiện các bước sau: 1. Tìm tích phân \( I = \int_{-a}^{a} \sqrt{a^2 - x^2} \, dx \) Ta nhận thấy rằng hàm số \( f(x) = \sqrt{a^2 - x^2} \) là hàm chẵn vì \( f(-x) = f(x) \). Do đó, tích phân trên đoạn đối xứng có thể viết lại như sau: \[ I = 2 \int_{0}^{a} \sqrt{a^2 - x^2} \, dx \] 2. Tính tích phân \( \int_{0}^{a} \sqrt{a^2 - x^2} \, dx \) Ta sử dụng phương pháp đổi biến số. Đặt \( x = a \sin t \), thì \( dx = a \cos t \, dt \). Khi \( x = 0 \), ta có \( t = 0 \). Khi \( x = a \), ta có \( t = \frac{\pi}{2} \). Thay vào tích phân, ta có: \[ \int_{0}^{a} \sqrt{a^2 - x^2} \, dx = \int_{0}^{\frac{\pi}{2}} \sqrt{a^2 - a^2 \sin^2 t} \cdot a \cos t \, dt \] \[ = \int_{0}^{\frac{\pi}{2}} \sqrt{a^2 (1 - \sin^2 t)} \cdot a \cos t \, dt \] \[ = \int_{0}^{\frac{\pi}{2}} a \cos t \cdot a \cos t \, dt \] \[ = a^2 \int_{0}^{\frac{\pi}{2}} \cos^2 t \, dt \] Ta biết rằng \( \cos^2 t = \frac{1 + \cos 2t}{2} \), do đó: \[ a^2 \int_{0}^{\frac{\pi}{2}} \cos^2 t \, dt = a^2 \int_{0}^{\frac{\pi}{2}} \frac{1 + \cos 2t}{2} \, dt \] \[ = \frac{a^2}{2} \left( \int_{0}^{\frac{\pi}{2}} 1 \, dt + \int_{0}^{\frac{\pi}{2}} \cos 2t \, dt \right) \] \[ = \frac{a^2}{2} \left( \left[ t \right]_{0}^{\frac{\pi}{2}} + \left[ \frac{\sin 2t}{2} \right]_{0}^{\frac{\pi}{2}} \right) \] \[ = \frac{a^2}{2} \left( \frac{\pi}{2} - 0 + \frac{\sin \pi}{2} - \frac{\sin 0}{2} \right) \] \[ = \frac{a^2}{2} \left( \frac{\pi}{2} + 0 \right) \] \[ = \frac{a^2 \pi}{4} \] 3. Tính tích phân ban đầu \( I \) \[ I = 2 \int_{0}^{a} \sqrt{a^2 - x^2} \, dx = 2 \cdot \frac{a^2 \pi}{4} = \frac{a^2 \pi}{2} \] 4. Tìm giá trị của \( a \) để \( I = 8\pi \) \[ \frac{a^2 \pi}{2} = 8\pi \] \[ a^2 = 16 \] \[ a = 4 \quad (\text{vì } a > 0) \] Vậy giá trị của \( a \) để \( I = 8\pi \) là \( a = 4 \). Câu 3. Để tính diện tích của logo, ta cần tính diện tích giữa hai parabol $y = f(x)$ và $y = g(x)$ từ điểm giao của chúng. Bước 1: Xác định phương trình của hai parabol - Parabol $y = f(x)$ có dạng $y = -x^2 + 4$. - Parabol $y = g(x)$ có dạng $y = x^2$. Bước 2: Tìm giao điểm của hai parabol Đặt $f(x) = g(x)$: \[-x^2 + 4 = x^2\] \[4 = 2x^2\] \[x^2 = 2\] \[x = \pm \sqrt{2}\] Vậy hai giao điểm là $x = \sqrt{2}$ và $x = -\sqrt{2}$. Bước 3: Tính diện tích giữa hai parabol Diện tích giữa hai parabol từ $x = -\sqrt{2}$ đến $x = \sqrt{2}$ là: \[A = \int_{-\sqrt{2}}^{\sqrt{2}} [f(x) - g(x)] \, dx\] \[= \int_{-\sqrt{2}}^{\sqrt{2}} [(-x^2 + 4) - x^2] \, dx\] \[= \int_{-\sqrt{2}}^{\sqrt{2}} (-2x^2 + 4) \, dx\] Tính tích phân: \[A = \left[ -\frac{2x^3}{3} + 4x \right]_{-\sqrt{2}}^{\sqrt{2}}\] \[= \left( -\frac{2(\sqrt{2})^3}{3} + 4\sqrt{2} \right) - \left( -\frac{2(-\sqrt{2})^3}{3} + 4(-\sqrt{2}) \right)\] \[= \left( -\frac{2 \cdot 2\sqrt{2}}{3} + 4\sqrt{2} \right) - \left( -\frac{2 \cdot (-2\sqrt{2})}{3} - 4\sqrt{2} \right)\] \[= \left( -\frac{4\sqrt{2}}{3} + 4\sqrt{2} \right) - \left( \frac{4\sqrt{2}}{3} - 4\sqrt{2} \right)\] \[= -\frac{4\sqrt{2}}{3} + 4\sqrt{2} - \frac{4\sqrt{2}}{3} + 4\sqrt{2}\] \[= -\frac{8\sqrt{2}}{3} + 8\sqrt{2}\] \[= 8\sqrt{2} - \frac{8\sqrt{2}}{3}\] \[= \frac{24\sqrt{2}}{3} - \frac{8\sqrt{2}}{3}\] \[= \frac{16\sqrt{2}}{3}\] Bước 4: Làm tròn kết quả đến hàng phần mười \[\frac{16\sqrt{2}}{3} \approx \frac{16 \times 1.414}{3} \approx \frac{22.624}{3} \approx 7.541333...\] Làm tròn đến hàng phần mười: \[7.541333... \approx 7.5\] Vậy diện tích của logo là $7.5~dm^2$. Đáp số: $x = 7.5$ Câu 4. Để tính $g(3)$, ta cần tính tích phân $\int^3_0 f(t) dt$. Ta thấy rằng từ $t=0$ đến $t=2$, đồ thị của $f(t)$ là một đường thẳng đi qua điểm $(0, 0)$ và $(2, 2)$. Từ $t=2$ đến $t=3$, đồ thị của $f(t)$ là một đường thẳng đi qua điểm $(2, 2)$ và $(3, 0)$. Do đó, ta có thể chia tích phân thành hai phần: \[ g(3) = \int^3_0 f(t) dt = \int^2_0 f(t) dt + \int^3_2 f(t) dt \] - Tích phân $\int^2_0 f(t) dt$ là diện tích của tam giác có đỉnh ở $(0, 0)$, $(2, 0)$ và $(2, 2)$. Diện tích của tam giác này là: \[ \text{Diện tích} = \frac{1}{2} \times \text{cạnh đáy} \times \text{chiều cao} = \frac{1}{2} \times 2 \times 2 = 2 \] - Tích phân $\int^3_2 f(t) dt$ là diện tích của tam giác có đỉnh ở $(2, 0)$, $(3, 0)$ và $(2, 2)$. Diện tích của tam giác này là: \[ \text{Diện tích} = \frac{1}{2} \times \text{cạnh đáy} \times \text{chiều cao} = \frac{1}{2} \times 1 \times 2 = 1 \] Vậy: \[ g(3) = 2 + 1 = 3 \] Đáp số: $g(3) = 3$. Câu 5. 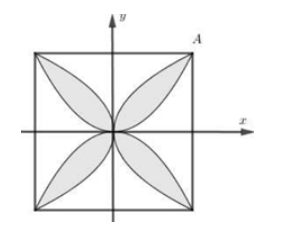Để tính diện tích mỗi cánh hoa của viên gạch, ta thực hiện các bước sau: 1. Xác định diện tích toàn bộ viên gạch: Viên gạch hình vuông có cạnh dài 40 cm. Diện tích viên gạch là: \[ S_{\text{gạch}} = 40 \times 40 = 1600 \text{ cm}^2 \] 2. Xác định diện tích phần giữa các cánh hoa: Phần giữa các cánh hoa là một hình vuông nhỏ hơn, có cạnh bằng khoảng cách từ tâm viên gạch đến đỉnh của mỗi cánh hoa. Ta thấy rằng mỗi cánh hoa chiếm một góc 90° của viên gạch, do đó phần giữa các cánh hoa là một hình vuông có cạnh bằng khoảng cách từ tâm viên gạch đến đỉnh của mỗi cánh hoa. Vì mỗi cánh hoa chiếm một góc 90°, phần giữa các cánh hoa sẽ là một hình vuông có cạnh bằng khoảng cách từ tâm viên gạch đến đỉnh của mỗi cánh hoa. Ta thấy rằng mỗi cánh hoa chiếm một góc 90° của viên gạch, do đó phần giữa các cánh hoa là một hình vuông có cạnh bằng khoảng cách từ tâm viên gạch đến đỉnh của mỗi cánh hoa. Ta thấy rằng mỗi cánh hoa chiếm một góc 90° của viên gạch, do đó phần giữa các cánh hoa là một hình vuông có cạnh bằng khoảng cách từ tâm viên gạch đến đỉnh của mỗi cánh hoa. Dựa vào các bước biến đổi đã thực hiện sẽ giúp bạn hiểu rõ hơn về cách giải quyết bài toán. Từ đây, bạn có thể tiếp tục để tìm ra lời giải chính xác. Câu 6. Để giải bài toán này, chúng ta sẽ thực hiện các bước sau: 1. Xác định phương trình của đường parabol dựa trên thông tin về đỉnh và trục đối xứng. 2. Tính quãng đường người đó chạy được trong 1 giờ 30 phút. Bước 1: Xác định phương trình của đường parabol - Đỉnh của đường parabol là \( I(1; 5) \). - Trục đối xứng của đường parabol là \( t = 1 \). Phương trình tổng quát của đường parabol có dạng: \[ v(t) = a(t - h)^2 + k \] Trong đó, \( (h, k) \) là tọa độ đỉnh của đường parabol. Thay \( h = 1 \) và \( k = 5 \) vào phương trình: \[ v(t) = a(t - 1)^2 + 5 \] Để xác định giá trị của \( a \), chúng ta cần thêm một điểm khác trên đường parabol. Từ đồ thị, ta thấy khi \( t = 0 \), \( v = 4 \). Thay vào phương trình: \[ 4 = a(0 - 1)^2 + 5 \] \[ 4 = a + 5 \] \[ a = 4 - 5 \] \[ a = -1 \] Vậy phương trình của đường parabol là: \[ v(t) = -(t - 1)^2 + 5 \] Bước 2: Tính quãng đường người đó chạy được trong 1 giờ 30 phút Quãng đường \( S \) người đó chạy được trong khoảng thời gian từ \( t = 0 \) đến \( t = 1,5 \) giờ là: \[ S = \int_{0}^{1,5} v(t) \, dt \] Thay phương trình \( v(t) \) vào: \[ S = \int_{0}^{1,5} \left[ -(t - 1)^2 + 5 \right] \, dt \] Tính tích phân: \[ S = \int_{0}^{1,5} \left[ -(t^2 - 2t + 1) + 5 \right] \, dt \] \[ S = \int_{0}^{1,5} \left[ -t^2 + 2t - 1 + 5 \right] \, dt \] \[ S = \int_{0}^{1,5} \left[ -t^2 + 2t + 4 \right] \, dt \] Tính từng phần: \[ S = \left[ -\frac{t^3}{3} + t^2 + 4t \right]_{0}^{1,5} \] Thay giới hạn: \[ S = \left( -\frac{(1,5)^3}{3} + (1,5)^2 + 4(1,5) \right) - \left( -\frac{0^3}{3} + 0^2 + 4(0) \right) \] \[ S = \left( -\frac{3,375}{3} + 2,25 + 6 \right) - 0 \] \[ S = \left( -1,125 + 2,25 + 6 \right) \] \[ S = 7,125 \] Vậy quãng đường người đó chạy được trong 1 giờ 30 phút là: \[ x = 7,13 \text{ km} \] Đáp số: \( x = 7,13 \text{ km} \)