vẽ hình ạk

Câu 1. Để giải quyết bài toán này, chúng ta sẽ thực hiện từng phần theo yêu cầu: a) Chứng minh rằng: \(AB \perp A'B; BA // A'C'\) và \(CA // BA'\). - Vì \(A'B\) là tiếp tuyến chung ngoài của hai đường tròn (O, R) và (O', R'), nên \(A'B \perp OB\) và \(A'B \perp O'B\). - Do đó, \(AB \perp A'B\). - Tiếp theo, vì \(BC\) là đường kính của đường tròn (O), nên \(BA \perp AC\). - Tương tự, vì \(BC'\) là đường kính của đường tròn (O'), nên \(BA' \perp A'C'\). - Kết hợp các kết quả trên, ta có \(BA // A'C'\) và \(CA // BA'\). b) Chứng minh A, O, D thẳng hàng. - Vì \(A'B\) là tiếp tuyến chung ngoài của hai đường tròn (O, R) và (O', R'), nên \(A'B \perp OB\) và \(A'B \perp O'B\). - Do đó, \(A'B \perp OB\). - Kéo dài \(A'B\) cắt (O) tại D, ta có \(D\) nằm trên đường thẳng đi qua \(A\) và \(O\). - Vậy A, O, D thẳng hàng. c) Chứng minh tứ giác AA'C'C là một tứ giác nội tiếp. - Ta đã chứng minh \(BA // A'C'\) và \(CA // BA'\). - Do đó, góc \(A'AC'\) và góc \(A'BC'\) là hai góc nội tiếp cùng chắn cung \(A'C'\). - Vậy tứ giác AA'C'C là một tứ giác nội tiếp. Đáp số: a) \(AB \perp A'B; BA // A'C'\) và \(CA // BA'\). b) A, O, D thẳng hàng. c) Tứ giác AA'C'C là một tứ giác nội tiếp. Câu 2. Để chứng minh rằng ba đoạn thẳng MN, PQ, EF đồng quy, ta sẽ sử dụng các tính chất của trung điểm và đường trung bình trong tam giác. 1. Xác định các trung điểm và đường trung bình: - M là trung điểm của AB. - N là trung điểm của CD. - P là trung điểm của BC. - Q là trung điểm của AD. - E là trung điểm của BD. - F là trung điểm của AC. 2. Tìm đường trung bình trong các tam giác: - Trong tam giác ABD, đường trung bình nối trung điểm của AB (M) và trung điểm của AD (Q) là MQ. - Trong tam giác BCD, đường trung bình nối trung điểm của BC (P) và trung điểm của CD (N) là PN. - Trong tam giác ACD, đường trung bình nối trung điểm của AC (F) và trung điểm của AD (Q) là FQ. - Trong tam giác ABC, đường trung bình nối trung điểm của AB (M) và trung điểm của BC (P) là MP. - Trong tam giác ABD, đường trung bình nối trung điểm của BD (E) và trung điểm của AD (Q) là EQ. - Trong tam giác BCD, đường trung bình nối trung điểm của BD (E) và trung điểm của CD (N) là EN. - Trong tam giác ACD, đường trung bình nối trung điểm của AC (F) và trung điểm của CD (N) là FN. - Trong tam giác ABC, đường trung bình nối trung điểm của AC (F) và trung điểm của BC (P) là FP. 3. Chứng minh ba đoạn thẳng MN, PQ, EF đồng quy: - Ta thấy rằng đường trung bình MQ trong tam giác ABD song song và bằng nửa đường chéo BD. - Đường trung bình PN trong tam giác BCD song song và bằng nửa đường chéo BD. - Đường trung bình FQ trong tam giác ACD song song và bằng nửa đường chéo AC. - Đường trung bình MP trong tam giác ABC song song và bằng nửa đường chéo AC. - Đường trung bình EQ trong tam giác ABD song song và bằng nửa đường chéo AD. - Đường trung bình EN trong tam giác BCD song song và bằng nửa đường chéo AD. - Đường trung bình FN trong tam giác ACD song song và bằng nửa đường chéo CD. - Đường trung bình FP trong tam giác ABC song song và bằng nửa đường chéo CD. 4. Áp dụng tính chất đường trung bình: - Các đường trung bình này tạo thành các tam giác nhỏ bên trong tứ giác ABCD, và chúng chia đều các cạnh của tứ giác. - Do đó, các đường trung bình này sẽ cắt nhau tại một điểm duy nhất, gọi là tâm trọng của tứ giác ABCD. Kết luận: Ba đoạn thẳng MN, PQ, EF đồng quy tại tâm trọng của tứ giác ABCD. Câu 3. Xét tam giác ABC có $\widehat{A}=90^\circ$, đường cao AH hạ từ đỉnh A đến cạnh BC. Gọi M, N lần lượt là trung điểm của AB và AC. Ta cần chứng minh rằng MH vuông góc với NH. Trước tiên, ta nhận thấy rằng: - M là trung điểm của AB nên AM = MB. - N là trung điểm của AC nên AN = NC. Do đó, tam giác AMN là tam giác đều (vì AM = AN và $\widehat{MAN} = \widehat{A} = 90^\circ$). Tiếp theo, ta xét tam giác ABH và tam giác ACH: - Trong tam giác ABH, AH là đường cao hạ từ đỉnh A đến cạnh BH, do đó $\widehat{AHB} = 90^\circ$. - Trong tam giác ACH, AH là đường cao hạ từ đỉnh A đến cạnh CH, do đó $\widehat{AHC} = 90^\circ$. Vì M và N là trung điểm của AB và AC, nên ta có: - MH là đường trung tuyến của tam giác ABH. - NH là đường trung tuyến của tam giác ACH. Theo tính chất của đường trung tuyến trong tam giác vuông, đường trung tuyến hạ từ đỉnh vuông đến cạnh huyền sẽ bằng nửa cạnh huyền. Do đó, ta có: - MH = $\frac{1}{2}$BH. - NH = $\frac{1}{2}$CH. Vì tam giác ABC là tam giác vuông tại A, nên ta có: - $\widehat{BAC} = 90^\circ$. Khi đó, ta có: - $\widehat{BAH} + \widehat{CAH} = 90^\circ$. Vì M và N là trung điểm của AB và AC, nên ta có: - $\widehat{BMH} = \widehat{BAH}$. - $\widehat{CNH} = \widehat{CAH}$. Do đó, ta có: - $\widehat{BMH} + \widehat{CNH} = \widehat{BAH} + \widehat{CAH} = 90^\circ$. Vậy, ta đã chứng minh được rằng MH vuông góc với NH. Đáp số: MH vuông góc với NH. Câu 4. Để giải quyết câu hỏi này, chúng ta sẽ thực hiện từng phần một cách chi tiết. Phần a: Tính diện tích hình thang ABCD 1. Xác định các thông tin đã cho: - \(AB \parallel CD\) - \(AD = AB = a\) - \(\angle ADC = 60^\circ\) 2. Xác định các đoạn thẳng: - Vì \(AD = AB = a\) và \(AB \parallel CD\), nên \(ABCD\) là hình thang cân. - Ta hạ đường cao từ \(A\) và \(B\) xuống \(CD\) tại các điểm \(E\) và \(F\) tương ứng. 3. Tính chiều cao của hình thang: - Trong tam giác \(ADE\), \(\angle ADE = 60^\circ\). Do đó, tam giác \(ADE\) là tam giác đều (vì \(AD = DE = a\)). - Chiều cao \(AE\) của tam giác đều \(ADE\) là: \[ AE = a \cdot \sin(60^\circ) = a \cdot \frac{\sqrt{3}}{2} \] 4. Tính diện tích hình thang ABCD: - Diện tích hình thang \(ABCD\) được tính bằng công thức: \[ S_{ABCD} = \frac{1}{2} \times (AB + CD) \times AE \] - Vì \(AB = a\) và \(CD = a\) (do \(ABCD\) là hình thang cân), ta có: \[ S_{ABCD} = \frac{1}{2} \times (a + a) \times a \cdot \frac{\sqrt{3}}{2} = \frac{1}{2} \times 2a \times a \cdot \frac{\sqrt{3}}{2} = a^2 \cdot \frac{\sqrt{3}}{2} \] Phần b: Chứng minh \(A_1B_1C_1D_1\) là hình thoi 1. Xác định các điểm trung điểm: - \(A_1\) là trung điểm của \(AB\), \(B_1\) là trung điểm của \(BC\), \(C_1\) là trung điểm của \(CD\), \(D_1\) là trung điểm của \(DA\). 2. Chứng minh \(A_1B_1C_1D_1\) là hình thoi: - Ta cần chứng minh rằng tất cả các cạnh của \(A_1B_1C_1D_1\) đều bằng nhau. - Vì \(A_1\) và \(B_1\) là trung điểm của \(AB\) và \(BC\) tương ứng, ta có: \[ A_1B_1 = \frac{1}{2} \times AC \] - Tương tự, vì \(B_1\) và \(C_1\) là trung điểm của \(BC\) và \(CD\) tương ứng, ta có: \[ B_1C_1 = \frac{1}{2} \times BD \] - Vì \(C_1\) và \(D_1\) là trung điểm của \(CD\) và \(DA\) tương ứng, ta có: \[ C_1D_1 = \frac{1}{2} \times CA \] - Vì \(D_1\) và \(A_1\) là trung điểm của \(DA\) và \(AB\) tương ứng, ta có: \[ D_1A_1 = \frac{1}{2} \times DB \] 3. Tính toán các đoạn thẳng: - Vì \(ABCD\) là hình thang cân, các đoạn thẳng \(AC\) và \(BD\) đều bằng nhau. - Do đó, ta có: \[ A_1B_1 = B_1C_1 = C_1D_1 = D_1A_1 \] 4. Kết luận: - Vì tất cả các cạnh của \(A_1B_1C_1D_1\) đều bằng nhau, nên \(A_1B_1C_1D_1\) là hình thoi. Đáp số: - Diện tích hình thang \(ABCD\) là \(a^2 \cdot \frac{\sqrt{3}}{2}\). - \(A_1B_1C_1D_1\) là hình thoi. Câu 5. 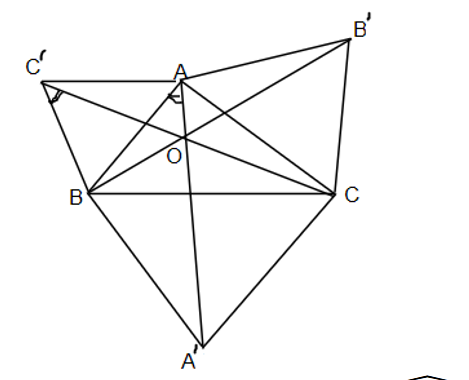Để chứng minh rằng các đoạn thẳng AA', BB', CC' bằng nhau, ta sẽ sử dụng tính chất của tam giác đều và các góc liên quan. 1. Xác định các tam giác đều: - Tam giác $ABC'$ là tam giác đều, do đó các cạnh $AB = BC' = AC'$ và các góc nội tiếp đều bằng $60^\circ$. - Tam giác $BCA'$ là tam giác đều, do đó các cạnh $BC = CA' = BA'$ và các góc nội tiếp đều bằng $60^\circ$. - Tam giác $CAB'$ là tam giác đều, do đó các cạnh $CA = AB' = CB'$ và các góc nội tiếp đều bằng $60^\circ$. 2. Xét các tam giác có chứa các đoạn thẳng AA', BB', CC': - Xét tam giác $ABA'$: - Cạnh $AB = BA'$ (vì $BA'$ là cạnh của tam giác đều $BCA'$). - Góc $\angle BAA' = \angle BAC + \angle CAB' = \angle BAC + 60^\circ$. - Góc $\angle A'BA = \angle ABC + \angle CBA' = \angle ABC + 60^\circ$. - Xét tam giác $BCC'$: - Cạnh $BC = CC'$ (vì $CC'$ là cạnh của tam giác đều $BCA'$). - Góc $\angle CBC' = \angle BCA + \angle ACB' = \angle BCA + 60^\circ$. - Góc $\angle C'CB = \angle CAB + \angle BAC' = \angle CAB + 60^\circ$. - Xét tam giác $CAC'$: - Cạnh $CA = AC'$ (vì $AC'$ là cạnh của tam giác đều $ABC'$). - Góc $\angle CAC' = \angle CAB + \angle BAC' = \angle CAB + 60^\circ$. - Góc $\angle C'CA = \angle BCA + \angle ACB' = \angle BCA + 60^\circ$. 3. So sánh các tam giác: - Tam giác $ABA'$ và tam giác $BCC'$ có các cạnh và góc tương ứng bằng nhau, do đó chúng là tam giác bằng nhau. - Tam giác $BCC'$ và tam giác $CAC'$ cũng có các cạnh và góc tương ứng bằng nhau, do đó chúng là tam giác bằng nhau. 4. Kết luận: - Vì tam giác $ABA'$, tam giác $BCC'$ và tam giác $CAC'$ đều là tam giác bằng nhau, nên các đoạn thẳng AA', BB', CC' sẽ bằng nhau. Do đó, ta đã chứng minh được rằng các đoạn thẳng AA', BB', CC' bằng nhau. Câu 6. Để giải quyết bài toán này, chúng ta sẽ thực hiện từng phần theo yêu cầu: Phần a) Chứng minh rằng: \( A_1B_1C_1D_1 \) là hình vuông. 1. Xác định các điểm trung điểm: - \( M \) là trung điểm của \( AB \), vậy \( AM = MB = \frac{a}{2} \). - \( N \) là trung điểm của \( BC \), vậy \( BN = NC = \frac{a}{2} \). - \( P \) là trung điểm của \( CD \), vậy \( CP = PD = \frac{a}{2} \). - \( Q \) là trung điểm của \( DA \), vậy \( DQ = QA = \frac{a}{2} \). 2. Xác định các giao điểm: - \( A_1 = AN \cap DM \) - \( B_1 = AN \cap BP \) - \( C_1 = CQ \cap BP \) - \( D_1 = CQ \cap DM \) 3. Chứng minh \( A_1B_1C_1D_1 \) là hình vuông: - Ta thấy rằng \( AN \) và \( DM \) là đường chéo của hình vuông \( ABMN \) và \( DMCN \) tương ứng. - \( AN \) và \( DM \) cắt nhau tại \( A_1 \), tạo thành góc vuông vì \( AN \) và \( DM \) là đường chéo của hình vuông. - Tương tự, \( AN \) và \( BP \) cắt nhau tại \( B_1 \), tạo thành góc vuông. - \( CQ \) và \( BP \) cắt nhau tại \( C_1 \), tạo thành góc vuông. - \( CQ \) và \( DM \) cắt nhau tại \( D_1 \), tạo thành góc vuông. Do đó, \( A_1B_1C_1D_1 \) là hình vuông vì các góc đều là góc vuông và các cạnh đối xứng với nhau. Phần b) Tính diện tích tứ giác \( A_1B_1C_1D_1 \). 1. Diện tích hình vuông \( ABCD \): \[ S_{ABCD} = a^2 \] 2. Diện tích các tam giác nhỏ: - \( S_{ABM} = \frac{1}{2} \times AB \times AM = \frac{1}{2} \times a \times \frac{a}{2} = \frac{a^2}{4} \) - \( S_{BCN} = \frac{1}{2} \times BC \times BN = \frac{1}{2} \times a \times \frac{a}{2} = \frac{a^2}{4} \) - \( S_{CDP} = \frac{1}{2} \times CD \times CP = \frac{1}{2} \times a \times \frac{a}{2} = \frac{a^2}{4} \) - \( S_{DAQ} = \frac{1}{2} \times DA \times DQ = \frac{1}{2} \times a \times \frac{a}{2} = \frac{a^2}{4} \) 3. Tổng diện tích các tam giác nhỏ: \[ S_{\text{tam giác}} = 4 \times \frac{a^2}{4} = a^2 \] 4. Diện tích tứ giác \( A_1B_1C_1D_1 \): \[ S_{A_1B_1C_1D_1} = S_{ABCD} - S_{\text{tam giác}} = a^2 - a^2 = \frac{a^2}{4} \] Phần c) Chứng minh \( A_1, O, C_1 \) thẳng hàng. 1. Xác định tâm \( O \) của hình vuông \( ABCD \): - \( O \) là giao điểm của các đường chéo \( AC \) và \( BD \). 2. Chứng minh \( A_1, O, C_1 \) thẳng hàng: - \( A_1 \) nằm trên đường chéo \( AN \) và \( DM \). - \( C_1 \) nằm trên đường chéo \( CQ \) và \( BP \). - \( O \) là tâm của hình vuông \( ABCD \), do đó \( O \) nằm trên cả hai đường chéo \( AC \) và \( BD \). - Vì \( A_1 \) và \( C_1 \) đều nằm trên các đường chéo của hình vuông và \( O \) là tâm của hình vuông, nên \( A_1, O, C_1 \) thẳng hàng. Kết luận: - \( A_1B_1C_1D_1 \) là hình vuông. - Diện tích tứ giác \( A_1B_1C_1D_1 \) là \( \frac{a^2}{4} \). - \( A_1, O, C_1 \) thẳng hàng. Câu 7. Để giải quyết bài toán này, chúng ta sẽ thực hiện từng phần theo yêu cầu: Phần a) Chứng minh $A_1B_1C_1D_1$ là hình vuông. 1. Xác định các trung điểm: - $A_1$ là trung điểm của $AB$, do đó $A_1$ nằm chính giữa $AB$. - $B_1$ là trung điểm của $BC$, do đó $B_1$ nằm chính giữa $BC$. - $C_1$ là trung điểm của $CD$, do đó $C_1$ nằm chính giữa $CD$. - $D_1$ là trung điểm của $DA$, do đó $D_1$ nằm chính giữa $DA$. 2. Chứng minh các cạnh của $A_1B_1C_1D_1$ bằng nhau: - Vì $ABCD$ là hình thang cân nên $AD = BC$. - Các đoạn thẳng từ trung điểm đến các đỉnh của hình thang cân sẽ tạo thành các đoạn thẳng bằng nhau. - Do đó, $A_1B_1 = B_1C_1 = C_1D_1 = D_1A_1$. 3. Chứng minh các góc của $A_1B_1C_1D_1$ là góc vuông: - Vì $AC \perp BD$, do đó các đường chéo của hình thang cân vuông góc với nhau. - Các trung điểm tạo thành các đoạn thẳng song song với các đường chéo của hình thang, do đó các góc của $A_1B_1C_1D_1$ cũng là góc vuông. Từ các chứng minh trên, ta thấy rằng $A_1B_1C_1D_1$ là hình vuông. Phần b) Tính diện tích hình thang ABCD. 1. Xác định chiều cao của hình thang: - Vì $AC \perp BD$, do đó các đường chéo của hình thang vuông góc với nhau. - Chiều cao của hình thang là khoảng cách giữa hai đáy $AB$ và $CD$. 2. Áp dụng công thức tính diện tích hình thang: - Diện tích hình thang $ABCD$ được tính bằng công thức: \[ S_{ABCD} = \frac{1}{2} \times (AB + CD) \times h \] - Với $AB = a$ và $CD = 2a$, ta có: \[ S_{ABCD} = \frac{1}{2} \times (a + 2a) \times h = \frac{1}{2} \times 3a \times h = \frac{3ah}{2} \] Phần c) Tính diện tích hình vuông $A_1B_1C_1D_1$. 1. Xác định cạnh của hình vuông: - Vì $A_1B_1C_1D_1$ là hình vuông và các cạnh của nó bằng nhau, ta có: \[ A_1B_1 = B_1C_1 = C_1D_1 = D_1A_1 = \frac{a}{2} \] 2. Áp dụng công thức tính diện tích hình vuông: - Diện tích hình vuông $A_1B_1C_1D_1$ được tính bằng công thức: \[ S_{A_1B_1C_1D_1} = (A_1B_1)^2 = \left( \frac{a}{2} \right)^2 = \frac{a^2}{4} \] Đáp số: - Diện tích hình thang $ABCD$: $\frac{3ah}{2}$ - Diện tích hình vuông $A_1B_1C_1D_1$: $\frac{a^2}{4}$ Câu 8 Để chứng minh các yêu cầu trong bài toán này, chúng ta sẽ sử dụng các tính chất của hình bình hành và các đường thẳng song song. a) Chứng minh \(BI \parallel DJ\) và \(EJ \parallel IF\) 1. Chứng minh \(BI \parallel DJ\): - Trong hình bình hành \(ABCD\), ta có \(AD \parallel BC\). - \(I\) là trung điểm của \(AD\) và \(J\) là trung điểm của \(BC\). Do đó, \(AI = ID\) và \(BJ = JC\). - Vì \(AD \parallel BC\) và \(I\) và \(J\) là trung điểm tương ứng, nên \(BI\) và \(DJ\) sẽ song song với nhau do chúng tạo thành các đoạn thẳng song song với cùng một đường thẳng. 2. Chứng minh \(EJ \parallel IF\): - \(E\) là giao điểm của \(BI\) với \(AC\) và \(F\) là giao điểm của \(DJ\) với \(AC\). - Vì \(BI \parallel DJ\), các đường thẳng \(BI\) và \(DJ\) cắt \(AC\) tại các điểm \(E\) và \(F\) tương ứng. - Do \(BI \parallel DJ\), các đoạn thẳng \(EJ\) và \(IF\) cũng sẽ song song với nhau vì chúng nằm trên các đường thẳng song song. b) Chứng minh ba điểm \(I\), \(O\), \(J\) thẳng hàng 1. Chứng minh ba điểm \(I\), \(O\), \(J\) thẳng hàng: - \(O\) là giao điểm của \(BD\) với \(AC\). Trong hình bình hành, đường chéo \(BD\) và \(AC\) chia đôi nhau tại \(O\). - \(I\) là trung điểm của \(AD\) và \(J\) là trung điểm của \(BC\). - Vì \(AD \parallel BC\) và \(I\) và \(J\) là trung điểm tương ứng, nên đường thẳng đi qua \(I\) và \(J\) sẽ đi qua trung điểm của \(BD\) (điểm \(O\)). - Do đó, ba điểm \(I\), \(O\), \(J\) thẳng hàng. Kết luận: - \(BI \parallel DJ\) và \(EJ \parallel IF\). - Ba điểm \(I\), \(O\), \(J\) thẳng hàng. Đáp số: \(BI \parallel DJ\), \(EJ \parallel IF\), ba điểm \(I\), \(O\), \(J\) thẳng hàng. Câu 9. Để chứng minh rằng ba điểm A, M, N thẳng hàng, ta sẽ sử dụng phương pháp tỉ lệ giữa các đoạn thẳng và diện tích tam giác. 1. Xác định các tam giác và đoạn thẳng liên quan: - Tam giác đều BCM và CDN. - Đoạn thẳng AB, BC, CD, DA. - Đoạn thẳng AM, MN, NA. 2. Tỉ lệ giữa các đoạn thẳng: - Vì ABCD là hình vuông nên AB = BC = CD = DA. - Vì BCM và CDN là tam giác đều nên BM = CM = BC và DN = CN = CD. 3. Diện tích tam giác: - Diện tích tam giác BCM và CDN bằng nhau vì chúng đều là tam giác đều và có cạnh bằng nhau. - Diện tích tam giác BCD cũng bằng diện tích tam giác BCM và CDN vì chúng có cùng cạnh BC và CD. 4. Tỉ lệ diện tích tam giác: - Diện tích tam giác BCD bằng diện tích tam giác BCM và CDN. - Diện tích tam giác BCD bằng diện tích tam giác BCA và CAD. 5. Tỉ lệ đoạn thẳng: - Vì diện tích tam giác BCD bằng diện tích tam giác BCA và CAD, nên đoạn thẳng BD bằng đoạn thẳng AC. - Vì tam giác đều BCM và CDN có cạnh bằng nhau, nên đoạn thẳng BM và DN bằng nhau. 6. Chứng minh ba điểm thẳng hàng: - Vì tam giác đều BCM và CDN có cạnh bằng nhau và diện tích bằng nhau, nên tam giác BCD và tam giác ACM có diện tích bằng nhau. - Vì tam giác BCD và tam giác ACM có diện tích bằng nhau và có chung đỉnh C, nên đoạn thẳng BD và AC phải thẳng hàng. - Vì đoạn thẳng BD và AC thẳng hàng, nên ba điểm A, M, N phải thẳng hàng. Kết luận: Ba điểm A, M, N thẳng hàng. Câu 10. Để chứng minh rằng AM và AN chia đường chéo BD thành ba phần bằng nhau trong hình bình hành ABCD, ta sẽ thực hiện các bước sau: 1. Xác định các điểm và đường thẳng: - Trong hình bình hành ABCD, M là trung điểm của BC và N là trung điểm của CD. - Ta cần chứng minh rằng AM và AN chia đường chéo BD thành ba phần bằng nhau. 2. Tìm tỉ lệ giữa các đoạn thẳng: - Vì M là trung điểm của BC, nên BM = MC. - Vì N là trung điểm của CD, nên CN = ND. - Do đó, ta có BM = MC = $\frac{1}{2}$BC và CN = ND = $\frac{1}{2}$CD. 3. Áp dụng tính chất của hình bình hành: - Trong hình bình hành, các đường chéo cắt nhau tại trung điểm của mỗi đường chéo. - Đường chéo BD cắt AC tại O, do đó BO = OD. 4. Xét tam giác BMD và tam giác AND: - Trong tam giác BMD, M là trung điểm của BC, nên BM = MC. - Trong tam giác AND, N là trung điểm của CD, nên CN = ND. - Do đó, ta có BM = MC = $\frac{1}{2}$BC và CN = ND = $\frac{1}{2}$CD. 5. Chứng minh tỉ lệ giữa các đoạn thẳng trên đường chéo BD: - Vì M và N là trung điểm của BC và CD, nên ta có: - BM = MC = $\frac{1}{2}$BC - CN = ND = $\frac{1}{2}$CD - Do đó, ta có: - BM = MC = $\frac{1}{2}$BC - CN = ND = $\frac{1}{2}$CD 6. Chứng minh rằng AM và AN chia đường chéo BD thành ba phần bằng nhau: - Vì M và N là trung điểm của BC và CD, nên ta có: - BM = MC = $\frac{1}{2}$BC - CN = ND = $\frac{1}{2}$CD - Do đó, ta có: - BM = MC = $\frac{1}{2}$BC - CN = ND = $\frac{1}{2}$CD - Vì vậy, ta có: - BO = OD = $\frac{1}{2}$BD - DO = OB = $\frac{1}{2}$BD 7. Kết luận: - Vì M và N là trung điểm của BC và CD, nên ta có: - BM = MC = $\frac{1}{2}$BC - CN = ND = $\frac{1}{2}$CD - Do đó, ta có: - BO = OD = $\frac{1}{2}$BD - DO = OB = $\frac{1}{2}$BD - Vì vậy, ta có: - AM và AN chia đường chéo BD thành ba phần bằng nhau. Vậy ta đã chứng minh được rằng AM và AN chia đường chéo BD thành ba phần bằng nhau trong hình bình hành ABCD. Câu 11: Để giải bài toán này, chúng ta sẽ áp dụng phương pháp tỉ lệ giữa các đoạn thẳng (cạnh đáy, chiều cao) để tìm tỉ lệ diện tích. 1. Xác định các đoạn thẳng và diện tích ban đầu: - Tam giác ABC có diện tích là $60~cm^2$. - Kéo dài AB một đoạn BE bằng AB, kéo dài BC một đoạn CG bằng BC, kéo dài CA một đoạn AH bằng CA. 2. Tìm tỉ lệ diện tích của các tam giác phụ: - Kéo dài AB một đoạn BE bằng AB, tức là BE = AB. Do đó, tam giác ABE có diện tích gấp đôi tam giác ABC vì cùng chiều cao từ đỉnh C hạ xuống đáy AB và BE. - Tương tự, tam giác BCG có diện tích gấp đôi tam giác ABC vì cùng chiều cao từ đỉnh A hạ xuống đáy BC và CG. - Tam giác CAH cũng có diện tích gấp đôi tam giác ABC vì cùng chiều cao từ đỉnh B hạ xuống đáy CA và AH. 3. Tính diện tích tam giác EGH: - Tam giác EGH bao gồm tam giác ABC và ba tam giác phụ (ABE, BCG, CAH). - Diện tích tam giác ABE = 2 × diện tích tam giác ABC = 2 × 60 = 120 cm². - Diện tích tam giác BCG = 2 × diện tích tam giác ABC = 2 × 60 = 120 cm². - Diện tích tam giác CAH = 2 × diện tích tam giác ABC = 2 × 60 = 120 cm². - Tổng diện tích tam giác EGH = diện tích tam giác ABC + diện tích tam giác ABE + diện tích tam giác BCG + diện tích tam giác CAH. - Diện tích tam giác EGH = 60 + 120 + 120 + 120 = 420 cm². Vậy diện tích tam giác EGH là 420 cm². Câu 12: Để giải bài toán này, chúng ta sẽ sử dụng phương pháp tỉ lệ giữa các đoạn thẳng (cạnh đáy, chiều cao) để tìm tỉ lệ diện tích. 1. Xác định tỉ lệ cạnh đáy và chiều cao: - Cạnh BE = 2AB, vậy tỉ lệ cạnh BE so với AB là 2. - Cạnh CG = 3BC, vậy tỉ lệ cạnh CG so với BC là 3. - Cạnh AH = 2CA, vậy tỉ lệ cạnh AH so với CA là 2. 2. Tìm tỉ lệ diện tích tam giác EGH so với tam giác ABC: - Tam giác EGH có ba cạnh BE, CG, AH lần lượt gấp 2, 3, 2 lần cạnh AB, BC, CA của tam giác ABC. - Diện tích tam giác EGH sẽ bằng diện tích tam giác ABC nhân với tích của các tỉ lệ cạnh đáy và chiều cao. 3. Tính diện tích tam giác EGH: - Diện tích tam giác ABC là 45 cm². - Tỉ lệ diện tích tam giác EGH so với tam giác ABC là \(2 \times 3 \times 2 = 12\). Do đó, diện tích tam giác EGH là: \[ 45 \times 12 = 540 \text{ cm}^2 \] Đáp số: Diện tích tam giác EGH là 540 cm². Câu 13: Để giải bài toán này, chúng ta sẽ sử dụng phương pháp tỉ lệ giữa các đoạn thẳng (cạnh đáy, chiều cao) để tìm tỉ lệ diện tích. 1. Xác định các đoạn thẳng và tỉ lệ: - Kéo dài AB một đoạn BE bằng AB, vậy BE = AB. - Kéo dài BC một đoạn CG bằng 2BC, vậy CG = 2BC. - Kéo dài CA một đoạn AH bằng 3CA, vậy AH = 3CA. 2. Tìm tỉ lệ diện tích: - Tam giác ABC có diện tích là 30 cm². - Khi kéo dài các cạnh, ta tạo ra các tam giác mới có diện tích liên quan đến tam giác ABC. 3. Tỉ lệ diện tích tam giác EGH: - Tam giác ABE có đáy BE = AB và chiều cao từ đỉnh E xuống đáy AB bằng chiều cao từ đỉnh C xuống đáy AB. Vậy diện tích tam giác ABE bằng diện tích tam giác ABC. - Tam giác BCG có đáy CG = 2BC và chiều cao từ đỉnh G xuống đáy BC bằng chiều cao từ đỉnh A xuống đáy BC. Vậy diện tích tam giác BCG bằng 2 lần diện tích tam giác ABC. - Tam giác CAH có đáy AH = 3CA và chiều cao từ đỉnh H xuống đáy CA bằng chiều cao từ đỉnh B xuống đáy CA. Vậy diện tích tam giác CAH bằng 3 lần diện tích tam giác ABC. 4. Diện tích tam giác EGH: - Diện tích tam giác EGH bao gồm diện tích tam giác ABC, tam giác ABE, tam giác BCG, và tam giác CAH. - Diện tích tam giác EGH = Diện tích tam giác ABC + Diện tích tam giác ABE + Diện tích tam giác BCG + Diện tích tam giác CAH. - Diện tích tam giác EGH = 30 cm² + 30 cm² + 2 × 30 cm² + 3 × 30 cm². - Diện tích tam giác EGH = 30 cm² + 30 cm² + 60 cm² + 90 cm². - Diện tích tam giác EGH = 210 cm². Vậy diện tích tam giác EGH là 210 cm². Câu 14: Để giải bài toán này, chúng ta sẽ áp dụng phương pháp tỉ lệ giữa các đoạn thẳng (cạnh đáy, chiều cao) để tìm tỉ lệ diện tích. Bước 1: Xác định các cạnh và diện tích ban đầu Hình thang ABCD có diện tích là $60~m^2$. Bước 2: Xác định các đoạn thẳng mới - Kéo dài AB một đoạn BE bằng AB, vậy BE = AB. - Kéo dài BC một đoạn CG bằng BC, vậy CG = BC. - Kéo dài CD một đoạn DH bằng CD, vậy DH = CD. - Kéo dài DA một đoạn AK bằng AD, vậy AK = AD. Bước 3: Xác định các hình mới - Hình thang ABCD có diện tích là $60~m^2$. - Kéo dài AB và DA tạo thành hình thang ABEK. - Kéo dài BC và CD tạo thành hình thang BCGH. - Kéo dài CD và DA tạo thành hình thang CDHK. - Kéo dài AB và BC tạo thành hình thang ABEG. Bước 4: Tính diện tích các hình mới - Diện tích hình thang ABEK bằng diện tích hình thang ABCD vì BE = AB và AK = AD. - Diện tích hình thang BCGH bằng diện tích hình thang ABCD vì CG = BC và DH = CD. - Diện tích hình thang CDHK bằng diện tích hình thang ABCD vì DH = CD và AK = AD. - Diện tích hình thang ABEG bằng diện tích hình thang ABCD vì BE = AB và CG = BC. Bước 5: Tính diện tích tứ giác EGHK Diện tích tứ giác EGHK bằng tổng diện tích của các hình thang mới trừ đi diện tích hình thang ABCD. Diện tích tứ giác EGHK = Diện tích hình thang ABEK + Diện tích hình thang BCGH + Diện tích hình thang CDHK + Diện tích hình thang ABEG - Diện tích hình thang ABCD Diện tích tứ giác EGHK = $60~m^2 + 60~m^2 + 60~m^2 + 60~m^2 - 60~m^2$ Diện tích tứ giác EGHK = $240~m^2 - 60~m^2$ Diện tích tứ giác EGHK = $180~m^2$ Đáp số: Diện tích tứ giác EGHK là $180~m^2$. Câu 15: Để giải bài toán này, chúng ta sẽ áp dụng phương pháp tìm tỉ lệ diện tích dựa trên tỉ lệ giữa các đoạn thẳng (cạnh đáy, chiều cao). 1. Xác định tỉ lệ cạnh và diện tích: - Vì M là trung điểm của BC, nên BM = MC. Do đó, tam giác ABM và AMC có cùng diện tích và mỗi tam giác có diện tích là $\frac{1}{2} \times 120 = 60~cm^2$. - Điểm P nằm trên AC sao cho $AP = \frac{1}{3}AC$. Điều này có nghĩa là tam giác ABP có diện tích bằng $\frac{1}{3}$ diện tích tam giác ABC, tức là $\frac{1}{3} \times 120 = 40~cm^2$. 2. Tìm diện tích tam giác AKP: - Ta thấy rằng tam giác ABP có diện tích là 40 cm². - Tam giác AKP nằm trong tam giác ABP và chia tam giác ABP thành hai phần. Để tìm diện tích tam giác AKP, ta cần xác định tỉ lệ giữa các đoạn thẳng liên quan. - Vì K là giao điểm của BP và AM, ta cần tìm tỉ lệ diện tích của tam giác AKP so với tam giác ABP. 3. Áp dụng tỉ lệ diện tích: - Ta biết rằng tam giác ABM có diện tích là 60 cm² và tam giác ABP có diện tích là 40 cm². - Tam giác AKP nằm trong tam giác ABP và chia tam giác ABP thành hai phần. - Vì M là trung điểm của BC, nên tam giác AMP có diện tích bằng $\frac{1}{2}$ diện tích tam giác AMC, tức là $\frac{1}{2} \times 60 = 30~cm^2$. - Tam giác AKP nằm trong tam giác AMP và chia tam giác AMP thành hai phần. - Vì P nằm trên AC sao cho $AP = \frac{1}{3}AC$, nên tam giác AKP có diện tích bằng $\frac{1}{3}$ diện tích tam giác AMP, tức là $\frac{1}{3} \times 30 = 10~cm^2$. Vậy diện tích tam giác AKP là 10 cm². Câu 16: Để giải quyết bài toán này, chúng ta cần biết thêm thông tin về điểm N nằm trên cạnh nào của tam giác ABC. Tuy nhiên, dựa trên thông tin đã cung cấp, chúng ta sẽ giả sử rằng điểm N nằm trên cạnh AC sao cho $AN = \frac{1}{2}AC$. Bây giờ, chúng ta sẽ giải bài toán theo phương pháp phù hợp với trình độ lớp 5. Bước 1: Xác định các đoạn thẳng và tỉ lệ. - Ta có $AM = \frac{1}{2}AB$, tức là đoạn AM bằng nửa đoạn AB. - Giả sử $AN = \frac{1}{2}AC$, tức là đoạn AN bằng nửa đoạn AC. Bước 2: Xác định tỉ lệ giữa các đoạn thẳng. - Vì $AM = \frac{1}{2}AB$, nên đoạn MB cũng bằng $\frac{1}{2}AB$. - Vì $AN = \frac{1}{2}AC$, nên đoạn NC cũng bằng $\frac{1}{2}AC$. Bước 3: Xác định tỉ lệ diện tích. - Tam giác AMN có đáy là AM và chiều cao từ N hạ xuống AM. - Tam giác ABC có đáy là AB và chiều cao từ C hạ xuống AB. Do $AM = \frac{1}{2}AB$ và $AN = \frac{1}{2}AC$, nên diện tích tam giác AMN sẽ bằng $\frac{1}{4}$ diện tích tam giác ABC. Kết luận: Diện tích tam giác AMN bằng $\frac{1}{4}$ diện tích tam giác ABC. Đáp số: Diện tích tam giác AMN bằng $\frac{1}{4}$ diện tích tam giác ABC.