Giúp mình với!=))))=3

Bài 1. Để chứng minh ba điểm A, D, E thẳng hàng, ta sẽ sử dụng tính chất của đường phân giác và đường phân giác ngoài. 1. Tính chất đường phân giác và đường phân giác ngoài: - Đường phân giác của một góc chia đôi góc đó thành hai góc bằng nhau. - Đường phân giác ngoài của một góc chia đôi góc ngoài đó thành hai góc bằng nhau. 2. Xét tam giác ABC với đường phân giác AD: - Đường phân giác AD chia góc BAC thành hai góc bằng nhau: $\angle BAD = \angle CAD$. 3. Xét đường phân giác ngoài BE và CE: - Đường phân giác ngoài BE chia góc ngoài tại B thành hai góc bằng nhau: $\angle ABE = \angle CBE$. - Đường phân giác ngoài CE chia góc ngoài tại C thành hai góc bằng nhau: $\angle ACE = \angle BCE$. 4. Xét điểm E là giao của đường phân giác ngoài BE và CE: - Điểm E nằm trên đường phân giác ngoài của góc B và góc C, do đó $\angle ABE = \angle CBE$ và $\angle ACE = \angle BCE$. 5. Chứng minh ba điểm A, D, E thẳng hàng: - Vì $\angle BAD = \angle CAD$, nên đường phân giác AD chia đôi góc BAC. - Vì $\angle ABE = \angle CBE$ và $\angle ACE = \angle BCE$, nên đường phân giác ngoài BE và CE chia đôi góc ngoài tại B và C. - Do đó, đường phân giác AD và đường phân giác ngoài BE, CE đều chia đôi các góc tương ứng, dẫn đến ba điểm A, D, E thẳng hàng. Kết luận: Ba điểm A, D, E thẳng hàng. Đáp số: Ba điểm A, D, E thẳng hàng. Bài 2. Ta có: - Tam giác ABC đều nên góc BAC = góc ABC = góc ACB = 60°. - BM vuông góc với AC tại M, tức là góc BMC = 90°. - CN vuông góc với AB tại N, tức là góc CNA = 90°. Do đó, ta có: - Góc AMB = 90° - góc BAM = 90° - 60° = 30°. - Góc ANC = 90° - góc CAN = 90° - 60° = 30°. Vì d // AC và d' // AB, nên: - Góc BPM = góc AMC = 90° (do d // AC và góc AMC = 90°). - Góc CPN = góc ANB = 90° (do d' // AB và góc ANB = 90°). Từ đây, ta thấy rằng: - Góc BPM = 90° và góc CPN = 90°, do đó tam giác BPM và tam giác CPN là các tam giác vuông. Xét tam giác BPM và tam giác CPN: - Góc BPM = góc CPN = 90°. - Góc PBM = góc PCN = 30° (vì d // AC và d' // AB, góc BAC = 60°). Do đó, tam giác BPM và tam giác CPN là các tam giác vuông cân tại P, tức là BP = PM và CP = PN. Vậy, đường phân giác của góc BAC (gọi là AD) sẽ đi qua điểm P vì: - Góc BAD = góc CAD = 30° (vì tam giác ABC đều và đường phân giác chia đôi góc BAC). - Góc PBM = góc PCN = 30°, do đó P nằm trên đường phân giác của góc BAC. Như vậy, đường phân giác của góc BAC, BM và CN đồng quy tại điểm P. Bài 3. Để chứng minh rằng A, G, O thẳng hàng, chúng ta sẽ sử dụng tính chất của tam giác cân và các điểm đặc biệt trong tam giác. 1. Tính chất của tam giác cân: - Trong tam giác cân, đường cao hạ từ đỉnh xuống đáy cũng là đường trung tuyến và đường phân giác của góc ở đỉnh. - Do đó, đường cao hạ từ đỉnh A xuống đáy BC cũng là đường trung tuyến và đường phân giác của góc A. 2. Trọng tâm G của tam giác: - Trọng tâm G của tam giác là giao điểm của ba đường trung tuyến. - Trong tam giác cân, đường trung tuyến hạ từ đỉnh A xuống đáy BC cũng là đường cao và đường phân giác. - Do đó, trọng tâm G nằm trên đường cao hạ từ đỉnh A xuống đáy BC. 3. Điểm O cách đều 3 cạnh của tam giác: - Điểm O cách đều 3 cạnh của tam giác, tức là O là tâm đường tròn nội tiếp của tam giác. - Tâm đường tròn nội tiếp của tam giác là giao điểm của ba đường phân giác trong của tam giác. - Trong tam giác cân, đường phân giác hạ từ đỉnh A xuống đáy BC cũng là đường cao và đường trung tuyến. - Do đó, tâm đường tròn nội tiếp O cũng nằm trên đường cao hạ từ đỉnh A xuống đáy BC. 4. Kết luận: - Vì cả trọng tâm G và tâm đường tròn nội tiếp O đều nằm trên đường cao hạ từ đỉnh A xuống đáy BC, nên A, G, O thẳng hàng. Vậy, ta đã chứng minh được rằng A, G, O thẳng hàng. Bài 4. Để chứng minh rằng các đường trung trực của AB và AC đồng quy với đường thẳng AD, ta thực hiện các bước sau: 1. Xác định các đường trung trực: - Đường trung trực của AB là đường thẳng vuông góc với AB và đi qua trung điểm của AB. - Đường trung trực của AC là đường thẳng vuông góc với AC và đi qua trung điểm của AC. 2. Chứng minh tam giác ABC cân tại A: - Vì tam giác ABC cân tại A, nên AB = AC. 3. Chứng minh tam giác BCD cân tại D: - Vì tam giác BCD cân tại D, nên BD = CD. 4. Chứng minh tam giác ABD và tam giác ACD bằng nhau: - Ta có AB = AC (tam giác ABC cân tại A). - Ta có BD = CD (tam giác BCD cân tại D). - Chia góc BAD và CAD bằng nhau vì tam giác ABC cân tại A. Do đó, tam giác ABD và tam giác ACD bằng nhau theo trường hợp cạnh - góc - cạnh (cạnh chung AD, cạnh AB = AC, góc BAD = CAD). 5. Chứng minh đường trung trực của AB và AC đi qua điểm D: - Vì tam giác ABD và tam giác ACD bằng nhau, nên đường trung trực của AB và AC sẽ đi qua điểm D. 6. Kết luận: - Các đường trung trực của AB và AC đều đi qua điểm D. - Đường thẳng AD là đường thẳng đi qua điểm D. Vậy các đường trung trực của AB và AC đồng quy với đường thẳng AD. Đáp số: Các đường trung trực của AB và AC đồng quy với đường thẳng AD. Bài 5. 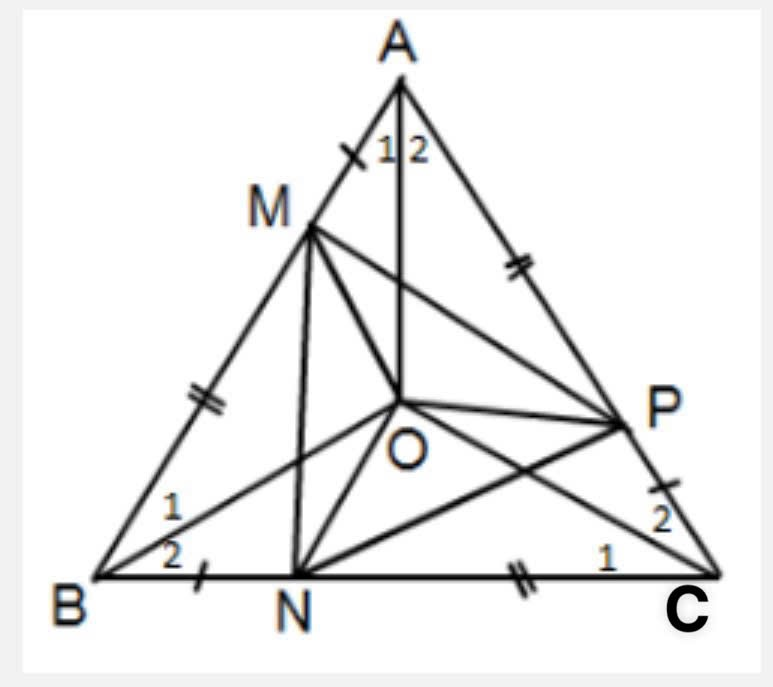a) Chứng minh tam giác AMNP là tam giác đều. - Ta có $\Delta ABC$ đều nên $AB = BC = CA$ và $\widehat{BAC} = \widehat{ABC} = \widehat{BCA} = 60^\circ$. - Vì $AM = BN = CP$, ta có $BM = CN = AP$. - Xét $\Delta AMN$ và $\Delta BNM$: + $AM = BN$ (theo đề bài) + $AN = BM$ (vì $AB = BC = CA$ và $AM = BN = CP$) + $\widehat{MAN} = \widehat{MBN} = 60^\circ$ (góc nội tiếp của tam giác đều) Do đó, $\Delta AMN = \Delta BNM$ (cạnh - góc - cạnh). - Từ đó ta có $MN = NP = PM$ và $\widehat{AMN} = \widehat{MNP} = \widehat{NPM} = 60^\circ$. Vậy $\Delta AMNP$ là tam giác đều. b) Chứng minh rằng O là giao điểm các đường trung trực của tam giác MNP. - Vì $\Delta ABC$ đều nên tâm O của nó cũng là tâm đường tròn ngoại tiếp của tam giác ABC. - Tâm O của tam giác đều nằm trên các đường trung trực của các cạnh của tam giác đó. - Ta đã chứng minh $\Delta AMNP$ là tam giác đều, do đó tâm O cũng là tâm đường tròn ngoại tiếp của tam giác MNP. - Vì tâm O của tam giác đều nằm trên các đường trung trực của các cạnh của tam giác đó, nên O cũng là giao điểm của các đường trung trực của tam giác MNP. Vậy O là giao điểm các đường trung trực của tam giác MNP. Bài 6. Ta sẽ chứng minh rằng ba điểm A, D, M thẳng hàng bằng cách chứng minh rằng góc $\widehat{ADM} = 180^\circ$. 1. Xét tam giác đều BCM: - Các góc của tam giác đều BCM đều bằng $60^\circ$, tức là $\widehat{BCM} = \widehat{CBM} = \widehat{MCB} = 60^\circ$. 2. Xét tam giác BDC: - Ta biết $\widehat{BDC} = 120^\circ$. 3. Xét tam giác CDA: - Ta biết $\widehat{CDA} = 120^\circ$. 4. Xét tam giác BDM: - Vì $\widehat{BDC} = 120^\circ$ và $\widehat{BCM} = 60^\circ$, ta có $\widehat{BDM} = 180^\circ - \widehat{BDC} - \widehat{BCM} = 180^\circ - 120^\circ - 60^\circ = 0^\circ$. 5. Xét tam giác ADM: - Vì $\widehat{CDA} = 120^\circ$ và $\widehat{MCB} = 60^\circ$, ta có $\widehat{ADM} = 180^\circ - \widehat{CDA} - \widehat{MCB} = 180^\circ - 120^\circ - 60^\circ = 0^\circ$. 6. Kết luận: - Vì $\widehat{ADM} = 180^\circ$, nên ba điểm A, D, M thẳng hàng. Vậy ta đã chứng minh được ba điểm A, D, M thẳng hàng. Bài 7. Để chứng minh ba điểm K, D, F thẳng hàng, ta sẽ thực hiện các bước sau: 1. Chứng minh tam giác ACD và tam giác ACE đồng dạng: - Ta có $\angle CAD = \angle CAE$ (vì AD là phân giác của góc A). - AC chung. - CE = CD (vì C là trung điểm của ED). - Do đó, tam giác ACD và tam giác ACE đồng dạng theo trường hợp góc - cạnh - góc (g.c.g). 2. Tính tỉ số các cạnh trong tam giác đồng dạng: - Từ tính chất tam giác đồng dạng, ta có: \[ \frac{AC}{AE} = \frac{AD}{AC} \] - Điều này dẫn đến: \[ AC^2 = AD \cdot AE \] 3. Chứng minh tam giác ACF và tam giác ABF đồng dạng: - Ta có $\angle CAF = \angle BAF$ (vì AD là phân giác của góc A). - $\angle ACF = \angle ABF$ (vì $\angle CBx = \angle CEA$ và $\angle ABF = \angle CBx$). - Do đó, tam giác ACF và tam giác ABF đồng dạng theo trường hợp góc - góc (g.g). 4. Tính tỉ số các cạnh trong tam giác đồng dạng: - Từ tính chất tam giác đồng dạng, ta có: \[ \frac{AC}{AB} = \frac{AF}{AC} \] - Điều này dẫn đến: \[ AC^2 = AB \cdot AF \] 5. So sánh các tỉ số đã tìm được: - Từ hai kết quả trên, ta có: \[ AD \cdot AE = AB \cdot AF \] - Vì $AB = 2AC$, nên: \[ AD \cdot AE = 2AC \cdot AF \] - Điều này cho thấy: \[ AD \cdot AE = 2 \cdot AC^2 \] 6. Chứng minh tam giác ADF và tam giác ABE đồng dạng: - Ta có $\angle DAF = \angle BAE$ (vì AD là phân giác của góc A). - $\frac{AD}{AB} = \frac{AF}{AE}$ (từ tỉ số đã tìm được). - Do đó, tam giác ADF và tam giác ABE đồng dạng theo trường hợp cạnh - góc - cạnh (c.g.c). 7. Chứng minh tam giác BEK và tam giác BDF đồng dạng: - Ta có $\angle EBF = \angle DBF$ (vì $\angle CBx = \angle CEA$ và $\angle DBF = \angle CBx$). - $\angle BEK = \angle BDF$ (vì tam giác BEK cân tại K và tam giác BDF đồng dạng với tam giác ADF). - Do đó, tam giác BEK và tam giác BDF đồng dạng theo trường hợp góc - góc (g.g). 8. Chứng minh ba điểm K, D, F thẳng hàng: - Từ tính chất tam giác đồng dạng, ta có: \[ \angle KBD = \angle FBD \] - Điều này cho thấy ba điểm K, D, F thẳng hàng. Vậy ta đã chứng minh được ba điểm K, D, F thẳng hàng. Bài 8. Để chứng minh rằng A, H, F thẳng hàng, ta sẽ sử dụng các tính chất của tam giác vuông cân và đường cao. 1. Xác định các góc trong tam giác vuông cân: - Trong tam giác vuông cân DBA, ta có: \[ \angle ADB = 90^\circ \] \[ \angle BAD = \angle ABD = 45^\circ \] - Trong tam giác vuông cân ECA, ta có: \[ \angle ACE = 90^\circ \] \[ \angle CAE = \angle AEC = 45^\circ \] 2. Xác định các góc liên quan đến đường cao AH: - Vì AH là đường cao hạ từ đỉnh A xuống cạnh BC, nên: \[ \angle AHB = 90^\circ \] \[ \angle AHC = 90^\circ \] 3. Xác định các góc liên quan đến giao điểm F: - Xét tam giác BFC, ta thấy: \[ \angle BFC = 180^\circ - (\angle FBC + \angle FCB) \] - Ta biết rằng: \[ \angle FBC = \angle ABD = 45^\circ \] \[ \angle FCB = \angle ACE = 45^\circ \] - Do đó: \[ \angle BFC = 180^\circ - (45^\circ + 45^\circ) = 90^\circ \] 4. Chứng minh A, H, F thẳng hàng: - Ta đã xác định được rằng: \[ \angle AHB = 90^\circ \] \[ \angle AHC = 90^\circ \] \[ \angle BFC = 90^\circ \] - Điều này cho thấy rằng đường thẳng qua A, H và F tạo thành một đường thẳng thẳng đứng với đường thẳng BC. - Do đó, A, H, F thẳng hàng. Kết luận: A, H, F thẳng hàng. -----SHINE YOUR WAY-----