Giúp mình với

Bài 1 1) Thay $x=1$ vào biểu thức $A$, ta được: \[ A = \frac{\sqrt{1} - 2}{\sqrt{1} + 9} = \frac{1 - 2}{1 + 9} = \frac{-1}{10} = -\frac{1}{10} \] 2) Rút gọn biểu thức $B$: Điều kiện xác định: $x > 0, x \neq 4$ \[ B = \frac{3\sqrt{x} - 6}{x - 2\sqrt{x}} + \frac{\sqrt{x} - 3}{\sqrt{x}} - \frac{1}{2 - \sqrt{x}} \] Chúng ta sẽ rút gọn từng phân thức: \[ \frac{3\sqrt{x} - 6}{x - 2\sqrt{x}} = \frac{3(\sqrt{x} - 2)}{\sqrt{x}(\sqrt{x} - 2)} = \frac{3}{\sqrt{x}} \] \[ \frac{\sqrt{x} - 3}{\sqrt{x}} = 1 - \frac{3}{\sqrt{x}} \] \[ \frac{1}{2 - \sqrt{x}} = \frac{1}{2 - \sqrt{x}} \cdot \frac{2 + \sqrt{x}}{2 + \sqrt{x}} = \frac{2 + \sqrt{x}}{4 - x} \] Do đó: \[ B = \frac{3}{\sqrt{x}} + 1 - \frac{3}{\sqrt{x}} - \frac{2 + \sqrt{x}}{4 - x} = 1 - \frac{2 + \sqrt{x}}{4 - x} \] \[ B = 1 - \frac{2 + \sqrt{x}}{4 - x} = \frac{(4 - x) - (2 + \sqrt{x})}{4 - x} = \frac{2 - x - \sqrt{x}}{4 - x} \] 3) Biểu thức $P = A \cdot B$: \[ P = \left( \frac{\sqrt{x} - 2}{\sqrt{x} + 9} \right) \left( \frac{2 - x - \sqrt{x}}{4 - x} \right) \] Ta cần tìm $x$ là số nguyên lớn nhất sao cho $P < \frac{1}{2}$: \[ \frac{\sqrt{x} - 2}{\sqrt{x} + 9} \cdot \frac{2 - x - \sqrt{x}}{4 - x} < \frac{1}{2} \] Chúng ta thử các giá trị $x$ nguyên lớn dần để tìm giá trị thỏa mãn: - Với $x = 1$: \[ P = \left( \frac{\sqrt{1} - 2}{\sqrt{1} + 9} \right) \left( \frac{2 - 1 - \sqrt{1}}{4 - 1} \right) = \left( \frac{1 - 2}{1 + 9} \right) \left( \frac{2 - 1 - 1}{3} \right) = \left( \frac{-1}{10} \right) \left( \frac{0}{3} \right) = 0 < \frac{1}{2} \] - Với $x = 2$: \[ P = \left( \frac{\sqrt{2} - 2}{\sqrt{2} + 9} \right) \left( \frac{2 - 2 - \sqrt{2}}{4 - 2} \right) = \left( \frac{\sqrt{2} - 2}{\sqrt{2} + 9} \right) \left( \frac{-\sqrt{2}}{2} \right) \] - Với $x = 3$: \[ P = \left( \frac{\sqrt{3} - 2}{\sqrt{3} + 9} \right) \left( \frac{2 - 3 - \sqrt{3}}{4 - 3} \right) = \left( \frac{\sqrt{3} - 2}{\sqrt{3} + 9} \right) \left( \frac{-1 - \sqrt{3}}{1} \right) \] - Với $x = 5$: \[ P = \left( \frac{\sqrt{5} - 2}{\sqrt{5} + 9} \right) \left( \frac{2 - 5 - \sqrt{5}}{4 - 5} \right) = \left( \frac{\sqrt{5} - 2}{\sqrt{5} + 9} \right) \left( \frac{-3 - \sqrt{5}}{-1} \right) = \left( \frac{\sqrt{5} - 2}{\sqrt{5} + 9} \right) \left( 3 + \sqrt{5} \right) \] Từ các phép tính trên, ta thấy $x = 5$ là số nguyên lớn nhất thỏa mãn $P < \frac{1}{2}$. Đáp số: $x = 5$. Bài 2 a) $3x^2+8x-3=0$ Ta có: $a=3$, $b=8$, $c=-3$ Tính $\Delta=b^2-4ac=8^2-4\times 3\times (-3)=100>0$ Phương trình có hai nghiệm phân biệt: $x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-8+10}{2\times 3}=\frac{1}{3}$ $x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-8-10}{2\times 3}=-3$ Vậy nghiệm của phương trình là $x_1=\frac{1}{3}$ và $x_2=-3$. b) $x^2-6x-7=0$ Ta có: $a=1$, $b=-6$, $c=-7$ Tính $\Delta=b^2-4ac=(-6)^2-4\times 1\times (-7)=64>0$ Phương trình có hai nghiệm phân biệt: $x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{6+8}{2\times 1}=7$ $x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{6-8}{2\times 1}=-1$ Vậy nghiệm của phương trình là $x_1=7$ và $x_2=-1$. c) $5x^2+2\sqrt{10}.x+2=0$ Ta có: $a=5$, $b=2\sqrt{10}$, $c=2$ Tính $\Delta=b^2-4ac=(2\sqrt{10})^2-4\times 5\times 2=0$ Phương trình có nghiệm kép: $x_1=x_2=\frac{-b}{2a}=\frac{-2\sqrt{10}}{2\times 5}=-\frac{\sqrt{10}}{5}$ Vậy nghiệm của phương trình là $x_1=x_2=-\frac{\sqrt{10}}{5}$. Bài 3 1) Gọi vận tốc lúc đầu của ô tô là $v$ (km/h, điều kiện: $v > 0$). Thời gian dự định đi từ A đến B là $\frac{120}{v}$ (giờ). Sau khi đi được 1 giờ, ô tô còn lại quãng đường là $120 - v$ (km). Do bị chặn 10 phút, tức là 0,17 giờ, nên thời gian còn lại để đi đến B là $\frac{120}{v} - 1 - 0,17 = \frac{120}{v} - 1,17$ (giờ). Với vận tốc mới là $v + 6$ (km/h), thời gian đi quãng đường còn lại là $\frac{120 - v}{v + 6}$ (giờ). Ta có phương trình: \[ \frac{120 - v}{v + 6} = \frac{120}{v} - 1,17 \] Nhân cả hai vế với $v(v + 6)$: \[ (120 - v)v = (120 - 1,17v)(v + 6) \] Phát triển và rút gọn: \[ 120v - v^2 = 120v + 720 - 1,17v^2 - 7,02v \] \[ -v^2 = 720 - 1,17v^2 - 7,02v \] \[ 0,17v^2 + 7,02v - 720 = 0 \] Chia cả phương trình cho 0,17: \[ v^2 + 41,29v - 4235,29 = 0 \] Giải phương trình bậc hai này bằng công thức: \[ v = \frac{-41,29 \pm \sqrt{41,29^2 + 4 \cdot 4235,29}}{2} \] \[ v = \frac{-41,29 \pm \sqrt{1704,86 + 16941,16}}{2} \] \[ v = \frac{-41,29 \pm \sqrt{18646,02}}{2} \] \[ v = \frac{-41,29 \pm 136,55}{2} \] Lấy nghiệm dương: \[ v = \frac{95,26}{2} = 47,63 \approx 48 \text{ (km/h)} \] Vậy vận tốc lúc đầu của ô tô là 48 km/h. 3) Biết rằng phương trình bậc hai $x^2 + x + m = 0$ có hai nghiệm là $x_1 = 1$ và $x_2$. Ta có: \[ 1 + x_2 = -1 \quad \text{(tổng các nghiệm)} \] \[ x_2 = -2 \] Biểu thức $A = 2024x_1 + 2025x_2$: \[ A = 2024 \cdot 1 + 2025 \cdot (-2) \] \[ A = 2024 - 4050 \] \[ A = -2026 \] Đáp số: $-2026$. Bài 4 1. a) Diện tích của hình quạt là: \[ S_{quạt} = \frac{150}{360} \times \pi \times 2^2 = \frac{5}{12} \times 4\pi = \frac{5\pi}{3} \text{dm}^2 \] b) Chiều dài cung của hình quạt là: \[ l_{cung} = \frac{150}{360} \times 2\pi \times 2 = \frac{5}{12} \times 4\pi = \frac{5\pi}{3} \text{dm} \] 2. a) Ta có $\angle BFC = \angle BEC = 90^\circ$, nên tứ giác BFEC nội tiếp. b) Ta có $\angle BFC = \angle BEC = 90^\circ$, nên $\angle ECF = \angle EBF$. Mà $\angle EBF = \angle OAC$ (góc nội tiếp và góc tâm cùng chắn cung AC), nên $\angle ECF = \angle OAC$. Do đó, OA vuông góc với EF. c) Ta có $\angle FHB = \angle FMB = \angle FNB$ (góc ngoài tam giác bằng tổng hai góc trong không kề), nên tứ giác AFHI nội tiếp. Ta có $\angle FHI = \angle FAI$ (góc nội tiếp cùng chắn cung FI), $\angle JAI = \angle JIA$ (tứ giác AFHI nội tiếp), $\angle JAI = \angle JKA$ (góc ngoài tam giác bằng tổng hai góc trong không kề), nên $\angle JKA = \angle JIA$, tức là ba điểm I, J, K thẳng hàng. Bài 5 Gọi số lần giảm giá là $x$ (lần, điều kiện: $x \geq 0$). Giá tour sau khi giảm là $2000000 - 100000x$ (đồng). Số người tham gia sau khi giảm giá là $150 + 20x$ (người). Doanh thu từ tour là: \[ A = (2000000 - 100000x)(150 + 20x) \] Ta có: \[ A = 2000000(150 + 20x) - 100000x(150 + 20x) \] \[ = 300000000 + 40000000x - 15000000x - 2000000x^2 \] \[ = 300000000 + 2500000x - 2000000x^2 \] Để doanh thu lớn nhất, ta cần tìm giá trị của $x$ sao cho $A$ đạt giá trị lớn nhất. Ta sử dụng phương pháp tìm giá trị lớn nhất của một biểu thức bậc hai. 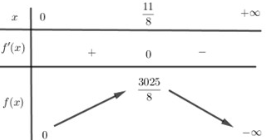Biểu thức $A = -2000000x^2 + 2500000x + 300000000$ là một biểu thức bậc hai có hệ số $a = -2000000 < 0$, nên nó đạt giá trị lớn nhất tại đỉnh của parabol. Đỉnh của parabol có hoành độ là: \[ x = -\frac{b}{2a} = -\frac{2500000}{2 \times (-2000000)} = \frac{2500000}{4000000} = \frac{5}{8} \] Vì $x$ phải là số nguyên, ta xét các giá trị gần $\frac{5}{8}$ nhất, đó là $x = 0$ và $x = 1$. - Khi $x = 0$: \[ A = 300000000 + 2500000 \times 0 - 2000000 \times 0^2 = 300000000 \] - Khi $x = 1$: \[ A = 300000000 + 2500000 \times 1 - 2000000 \times 1^2 = 300000000 + 2500000 - 2000000 = 300250000 \] Như vậy, doanh thu lớn nhất đạt được khi $x = 1$. Vậy công ty phải giảm giá tour là: \[ 100000 \times 1 = 100000 \text{ (đồng)} \] Đáp số: 100000 đồng.