cho nửa đường tròn tâm o đường kính AB cố định C là một điểm di chuyển trên nửa đường tròn

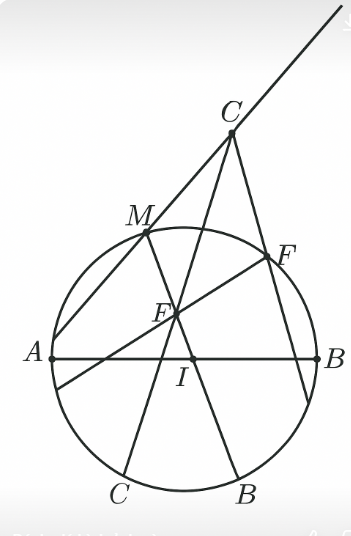
Câu 14. a) Ta có $\widehat{AIE}=\widehat{ACK}=90^\circ$ nên tứ giác AEIK nội tiếp (cùng chắn cung AK) b) Ta có $\widehat{MAO}=\widehat{CBK}$ (cùng phụ với $\widehat{BAC})$ $\widehat{AMO}=\widehat{BKC}=90^\circ$ nên $\Delta MAO\backsim\Delta CKB$ Tỉ số $\frac{AO}{BK}=\frac{OB}{BK}=\frac{AB}{2.BK}$ Diện tích S của 2 tam giác IAC và BCK là: $S=\frac{1}{2}.AC.IK+\frac{1}{2}.CK.BK$ $=\frac{1}{2}.AC.\frac{AO}{BK}.CK+\frac{1}{2}.CK.BK$ $=\frac{1}{2}.AC.\frac{AB}{2.BK}.CK+\frac{1}{2}.CK.BK$ $=\frac{1}{4}.AC.CK.\frac{AB}{BK}+\frac{1}{2}.CK.BK$ $=\frac{1}{4}.AC.CK.\frac{AB}{BK}+\frac{1}{4}.AC.CK.\frac{BK}{AB}$ $=\frac{1}{4}.AC.CK.(\frac{AB}{BK}+\frac{BK}{AB})$ Ta có $\frac{AB}{BK}+\frac{BK}{AB}\ge 2$ (theo Bất đẳng thức Cô-si) Dấu bằng xảy ra khi $\frac{AB}{BK}=\frac{BK}{AB}$ hay $BK=AB$ Khi đó diện tích S đạt giá trị lớn nhất. Vậy $\frac{FI}{AB}=\frac{BK}{AB}=\frac{1}{2}$