Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
27/08/2025
Giải hộ mình câu này với các bạn

 0
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



27/08/2025
 0
0
01/09/2025
Bài 2.1
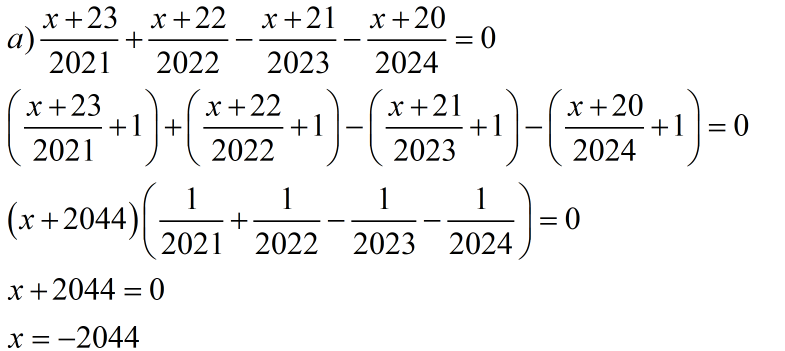
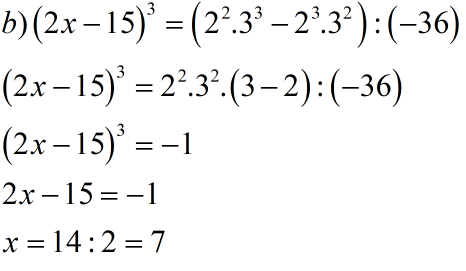
Bài 2.2
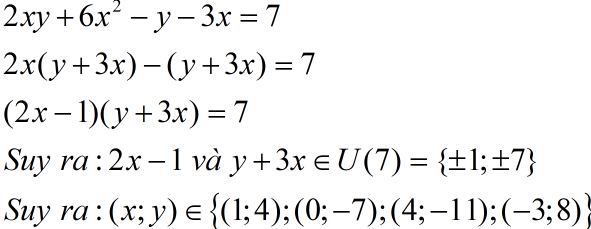
Bài 3.1
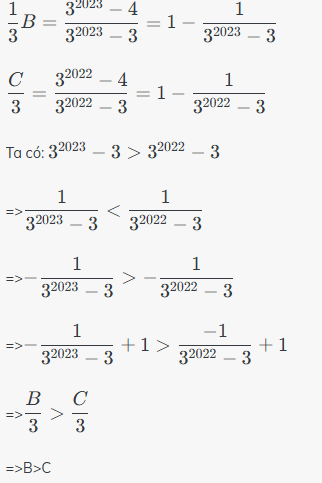
 0
0
27/08/2025
Bài 1.
Tính giá trị của biểu thức nếu có thể:
A =
((0,4 − 2/9 + 1/11 − 0,25 + 1/5) / (1,4 − 9/7 + 1/11 − 0,875 + 0,7))³ × (2013 / 2014)
Phân tích tử và mẫu:
Tử số:
0,4 = 4/10 = 2/5
0,25 = 1/4
=> 2/5 − 2/9 + 1/11 − 1/4 + 1/5
=> quy đồng rồi tính ra kết quả
Mẫu số:
1,4 = 14/10 = 7/5
0,875 = 7/8
=> 7/5 − 9/7 + 1/11 − 7/8 + 7/10
\=> quy đồng rồi tính ra kết quả
Sau đó chia tử cho mẫu, lấy kết quả lũy thừa 3 và nhân với 2013 / 2014.
=> Làm ra được giá trị cụ thể.
Tương tự với biểu thức:
B = 1/3 + 3/7 + 1/7.2 + 5/2.13 + 5/13.4.21
Cần biến đổi gọn và cộng các phân số lại.
Biểu thức C:
C = (2^12·3^5·4^9·6^2·5^10·7^3·25^4·9^2) / (2^2·3^6·8^4·35^2·(125·7)^3·5^9·14^3)
Phân tích các số dạng 4 = 2², 6 = 2×3, 25 = 5², 9 = 3², 8 = 2³, 35 = 5×7, 125 = 5³, 14 = 2×7,...
=> Rút gọn các lũy thừa, so sánh tử và mẫu, rồi rút gọn thành kết quả cuối cùng.
Bài 2.
Câu a)
Giải phương trình:
(x + 23)/2021 + (x + 22)/2022 + (x + 21)/2023 + (x + 20)/2024 = 0
Gộp lại:
x (1/2021 + 1/2022 + 1/2023 + 1/2024) + (23/2021 + 22/2022 + 21/2023 + 20/2024) = 0
=> x = - (23/2021 + 22/2022 + 21/2023 + 20/2024) / (1/2021 + 1/2022 + 1/2023 + 1/2024)
=> Tính toán cụ thể để ra x.
Câu b)
(2x − 15)¹³ = (2²·3 − 2²·3²) = 36
=> (2x − 15)¹³ = 36 → 2x − 15 = ∛(36)
36 không phải lũy thừa bậc 13 → Không có nghiệm nguyên
=> Không có x thỏa mãn
Bài 3.
Câu 1.
Cho B = 3^(2023−4) / 3^(2022−1) = 3^2019 / 3^2021 = 3^(-2)
=> B = 1 / 3² = 1/9
Cho C = 3^(2022−4) / 3^(2021−1) = 3^2018 / 3^2020 = 3^(-2) = 1/9
=> So sánh: B = C
Câu 2.
Giải hệ phương trình:
a + b + c = 0
CMR: 2022ab + 2023bc + 4045ca ≤ 0
Thay c = −a − b vào biểu thức:
2022ab + 2023b(−a − b) + 4045(−a − b)a
= 2022ab − 2023ab − 2023b² − 4045a² − 4045ab
= (2022 − 2023 − 4045)ab − 2023b² − 4045a²
= (−4046)ab − 2023b² − 4045a²
=> luôn ≤ 0 với mọi a, b
=> Đpcm
Bài 4.
Câu 1.
Thể tích bể nước hình hộp chữ nhật, có tỉ lệ R\:D\:C = 1:2:4
Tổng diện tích xung quanh: S = 112 m²
Gọi cạnh lần lượt là x, 2x, 4x
Diện tích xung quanh = 2(x·2x + x·4x + 2x·4x) = 2(x²·2 + x²·4 + x²·8) = 2x²·14 = 28x²
=> 28x² = 112 → x² = 4 → x = 2
=> V = x·2x·4x = 2·4·8 = 64 m³
Câu 2.
Chu vi HCN là 132m => 2(w + h) = 132 => w + h = 66
Giảm w 5m => w’ = w − 5
Tăng h 5m => h’ = h + 5
Mà h’ = 2w’ => h + 5 = 2(w − 5)
=> h + 5 = 2w − 10 => h = 2w − 15
Từ w + h = 66 => w + (2w − 15) = 66 => 3w = 81 => w = 27 => h = 39
Diện tích ban đầu: S = 27·39 = 1053
Diện tích trồng rau = 11/30 của diện tích => Diện tích xây nhà = 1 − 11/30 = 19/30
=> Diện tích xây nhà = 19/30 · 1053 = 666.7 m²
Câu 3.
Số cách chọn 2 điểm trong 2025 điểm: C(2025, 2)
=> Trừ đi số cặp điểm thẳng hàng (24 điểm): C(24, 2)
=> Đáp án = C(2025, 2) − C(24, 2) = (2025·2024)/2 − (24·23)/2 = 2,049,300 − 276 = 2,049,024 đường thẳng
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
2 giờ trước
2 giờ trước
Top thành viên trả lời



