Bài 5:
1) Ta có $\frac52=\frac yx$ và $x+y=-21.$
Ta có $\frac52=\frac yx=\frac{x+y}{2+5}=\frac{-21}{7}=-3$
Do đó $x=-3\times 2=-6,$ $y=-3\times 5=-15.$
2) Ta có $2x=3y=4z$ và $2x-5z=-6.$
Ta có $2x=3y=4z=\frac{2x-5z}{2-5}=\frac{-6}{-3}=2.$
Do đó $x=1,y=\frac23,z=\frac12.$
3) Ta có $\frac75=\frac yx$ và $x+y=-36.$
Ta có $\frac75=\frac yx=\frac{x+y}{7+5}=\frac{-36}{12}=-3.$
Do đó $x=-3\times 5=-15,$ $y=-3\times 7=-21.$
4) Ta có $2x=3y=4z$ và $x-y+z=35.$
Ta có $2x=3y=4z=\frac{x-y+z}{1-1,5+1}=\frac{35}{0,5}=70.$
Do đó $x=35,y=\frac{70}{3},z=17,5.$
5) Ta có $\frac xy=\frac2{-5}$ và $x-y=-7.$
Ta có $\frac xy=\frac2{-5}=\frac{x-y}{2+5}=\frac{-7}{7}=-1.$
Do đó $x=-2,y=5.$
6) Ta có $2x=3y=5z$ và $|x+y-z|=95.$
Ta có $2x=3y=5z=\frac{|x+y-z|}{0,5+1-1}=\frac{95}{0,5}=190.$
Do đó $x=95,y=\frac{190}{3},z=38.$
7) Ta có $x:y:z=4:3:9~va~x-3y+4z=62.$
Ta có $x:y:z=4:3:9=\frac{x-3y+4z}{4-9+36}=\frac{62}{31}=2.$
Do đó $x=8,y=6,z=18.$
8) Ta có $\frac\pi4=\frac3{12}=\frac z{15}$ và $y-x=4.$
Ta có $\frac\pi4=\frac3{12}=\frac z{15}=\frac{y-x}{3-4}=\frac4{-1}=-4.$
Do đó $x=-16,y=-12,z=-60.$
9) Ta có $3x=2y;7y=5z$ và $x-y+z=32.$
Ta có $3x=2y;7y=5z=\frac{x-y+z}{0,6-1+0,7}=\frac{32}{0,3}=106,67.$
Do đó $x=21,33,y=32,z=45,33.$
10) Ta có $\frac x2=\frac y3$ và $x^2+y^2=52.$
Ta có $\frac x2=\frac y3=\frac{\sqrt{x^2+y^2}}{\sqrt{4+9}}=\frac{\sqrt{52}}{\sqrt{13}}=\sqrt{4}=2.$
Do đó $x=4,y=6.$
11) Ta có $9x=10y;3z=4y$ và $x-y+z=78.$
Ta có $9x=10y;3z=4y=\frac{x-y+z}{0,9-1+1,33}=78:1,23=63,41.$
Do đó $x=70,45,y=63,41,z=84,55.$
11) Ta có $\frac x3=\frac y5$ và $x^2-y^2=-4.$
Ta có $\frac x3=\frac y5=\frac{\sqrt{x^2-y^2}}{\sqrt{9-25}}=\frac{\sqrt{-4}}{\sqrt{-16}}=\frac{i}{2i}=\frac12.$
Do đó $x=1,5,y=2,5.$
Bài 6:
1) Ta có $x:y:z=4:3:9$
Do đó ta có thể viết $x=4k$, $y=3k$, $z=9k$ với $k$ là hằng số.
Thay vào phương trình $x-3y+4z=62$, ta có:
$4k-3(3k)+4(9k)=62$
$4k-9k+36k=62$
$31k=62$
$k=2$
Vậy $x=4\times 2=8$, $y=3\times 2=6$, $z=9\times 2=18$.
2) Ta có $\frac{x}{4}=\frac{y}{12}=\frac{z}{15}$
Do đó ta có thể viết $x=4k$, $y=12k$, $z=15k$ với $k$ là hằng số.
Thay vào phương trình $y-x=4$, ta có:
$12k-4k=4$
$8k=4$
$k=0.5$
Vậy $x=4\times 0.5=2$, $y=12\times 0.5=6$, $z=15\times 0.5=7.5$.
3) Ta có $x:y:z=1:2:3$
Do đó ta có thể viết $x=k$, $y=2k$, $z=3k$ với $k$ là hằng số.
Thay vào phương trình $4x-3y+2z=36$, ta có:
$4k-3(2k)+2(3k)=36$
$4k-6k+6k=36$
$4k=36$
$k=9$
Vậy $x=9$, $y=2\times 9=18$, $z=3\times 9=27$.
4) Ta có $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$
Do đó ta có thể viết $x=2k$, $y=3k$, $z=4k$ với $k$ là hằng số.
Thay vào phương trình $4y-3x=12$, ta có:
$4(3k)-3(2k)=12$
$12k-6k=12$
$6k=12$
$k=2$
Vậy $x=2\times 2=4$, $y=3\times 2=6$, $z=4\times 2=8$.
5) Ta có $x:y:z=2:3:4$
Do đó ta có thể viết $x=2k$, $y=3k$, $z=4k$ với $k$ là hằng số.
Thay vào phương trình $x+2y-3z=-20$, ta có:
$2k+2(3k)-3(4k)=-20$
$2k+6k-12k=-20$
$-4k=-20$
$k=5$
Vậy $x=2\times 5=10$, $y=3\times 5=15$, $z=4\times 5=20$.
6) Ta có $\frac{x}{3}=\frac{y}{5}=\frac{z}{7}$
Do đó ta có thể viết $x=3k$, $y=5k$, $z=7k$ với $k$ là hằng số.
Thay vào phương trình $3y-2z=99$, ta có:
$3(5k)-2(7k)=99$
$15k-14k=99$
$k=99$
Vậy $x=3\times 99=297$, $y=5\times 99=495$, $z=7\times 99=693$.
7) Ta có $x:y:(-z)=3:8:5$
Do đó ta có thể viết $x=3k$, $y=8k$, $z=-5k$ với $k$ là hằng số.
Thay vào phương trình $4x+3y+2z=52$, ta có:
$4(3k)+3(8k)+2(-5k)=52$
$12k+24k-10k=52$
$26k=52$
$k=2$
Vậy $x=3\times 2=6$, $y=8\times 2=16$, $z=-5\times 2=-10$.
8) Ta có $\frac{x}{2}=\frac{y}{3}=\frac{z}{-4}$
Do đó ta có thể viết $x=2k$, $y=3k$, $z=-4k$ với $k$ là hằng số.
Thay vào phương trình $3x-2z=28$, ta có:
$3(2k)-2(-4k)=28$
$6k+8k=28$
$14k=28$
$k=2$
Vậy $x=2\times 2=4$, $y=3\times 2=6$, $z=-4\times 2=-8$.
9) Ta có $x:y:z=3:5:(-2)$
Do đó ta có thể viết $x=3k$, $y=5k$, $z=-2k$ với $k$ là hằng số.
Thay vào phương trình $5x-y+3z=124$, ta có:
$5(3k)-5k+3(-2k)=124$
$15k-5k-6k=124$
$4k=124$
$k=31$
Vậy $x=3\times 31=93$, $y=5\times 31=155$, $z=-2\times 31=-62$.
10) Ta có $\frac{x}{-3}=\frac{y}{-5}=\frac{z}{-4}$
Do đó ta có thể viết $x=-3k$, $y=-5k$, $z=-4k$ với $k$ là hằng số.
Thay vào phương trình $3z-2x=...$
Bài 7:
Câu hỏi:
Tìm x, y, z biết:
\[ 2,\frac{x}{2}=\frac{y}{3}, \quad x^2 + y^2 = 52, \quad x - y + z = 32. \]
\[ 1,~3x = 2y; \quad 7y = 5z \quad \text{và} \quad x - y + z = 78. \]
\[ 4,\frac{x}{3}=\frac{y}{5} \quad \text{và} \quad x^2 - y^2 = -4. \]
\[ 3,9x = 10y; \quad 3z = 4y \quad \text{và} \quad x - y + z = -15. \]
\[ 6\frac{x}{25}=\frac{y}{4} \quad \text{và} \quad x^2 - y^2 = 3. \]
Câu trả lời:
Bài 1:
\[ \frac{x}{2} = \frac{y}{3} \]
Ta có:
\[ x = \frac{2y}{3} \]
Thay vào phương trình \( x^2 + y^2 = 52 \):
\[ \left( \frac{2y}{3} \right)^2 + y^2 = 52 \]
\[ \frac{4y^2}{9} + y^2 = 52 \]
\[ \frac{4y^2 + 9y^2}{9} = 52 \]
\[ \frac{13y^2}{9} = 52 \]
\[ 13y^2 = 468 \]
\[ y^2 = 36 \]
\[ y = 6 \quad \text{(vì \( y > 0 \))} \]
Thay \( y = 6 \) vào \( x = \frac{2y}{3} \):
\[ x = \frac{2 \times 6}{3} = 4 \]
Thay \( x = 4 \) và \( y = 6 \) vào \( x - y + z = 32 \):
\[ 4 - 6 + z = 32 \]
\[ z = 34 \]
Vậy \( x = 4 \), \( y = 6 \), \( z = 34 \).
Bài 2:
\[ 3x = 2y \]
\[ 7y = 5z \]
\[ x - y + z = 78 \]
Ta có:
\[ x = \frac{2y}{3} \]
\[ z = \frac{7y}{5} \]
Thay vào phương trình \( x - y + z = 78 \):
\[ \frac{2y}{3} - y + \frac{7y}{5} = 78 \]
\[ \frac{10y - 15y + 21y}{15} = 78 \]
\[ \frac{16y}{15} = 78 \]
\[ 16y = 1170 \]
\[ y = 73.125 \]
Thay \( y = 73.125 \) vào \( x = \frac{2y}{3} \):
\[ x = \frac{2 \times 73.125}{3} = 48.75 \]
Thay \( y = 73.125 \) vào \( z = \frac{7y}{5} \):
\[ z = \frac{7 \times 73.125}{5} = 102.375 \]
Vậy \( x = 48.75 \), \( y = 73.125 \), \( z = 102.375 \).
Bài 3:
\[ \frac{x}{3} = \frac{y}{5} \]
\[ x^2 - y^2 = -4 \]
Ta có:
\[ x = \frac{3y}{5} \]
Thay vào phương trình \( x^2 - y^2 = -4 \):
\[ \left( \frac{3y}{5} \right)^2 - y^2 = -4 \]
\[ \frac{9y^2}{25} - y^2 = -4 \]
\[ \frac{9y^2 - 25y^2}{25} = -4 \]
\[ \frac{-16y^2}{25} = -4 \]
\[ -16y^2 = -100 \]
\[ y^2 = 6.25 \]
\[ y = 2.5 \quad \text{(vì \( y > 0 \))} \]
Thay \( y = 2.5 \) vào \( x = \frac{3y}{5} \):
\[ x = \frac{3 \times 2.5}{5} = 1.5 \]
Vậy \( x = 1.5 \), \( y = 2.5 \).
Bài 4:
\[ 9x = 10y \]
\[ 3z = 4y \]
\[ x - y + z = -15 \]
Ta có:
\[ x = \frac{10y}{9} \]
\[ z = \frac{4y}{3} \]
Thay vào phương trình \( x - y + z = -15 \):
\[ \frac{10y}{9} - y + \frac{4y}{3} = -15 \]
\[ \frac{10y - 9y + 12y}{9} = -15 \]
\[ \frac{13y}{9} = -15 \]
\[ 13y = -135 \]
\[ y = -10.38 \]
Thay \( y = -10.38 \) vào \( x = \frac{10y}{9} \):
\[ x = \frac{10 \times -10.38}{9} = -11.53 \]
Thay \( y = -10.38 \) vào \( z = \frac{4y}{3} \):
\[ z = \frac{4 \times -10.38}{3} = -13.84 \]
Vậy \( x = -11.53 \), \( y = -10.38 \), \( z = -13.84 \).
Bài 5:
\[ \frac{x}{25} = \frac{y}{4} \]
\[ x^2 - y^2 = 3 \]
Ta có:
\[ x = \frac{25y}{4} \]
Thay vào phương trình \( x^2 - y^2 = 3 \):
\[ \left( \frac{25y}{4} \right)^2 - y^2 = 3 \]
\[ \frac{625y^2}{16} - y^2 = 3 \]
\[ \frac{625y^2 - 16y^2}{16} = 3 \]
\[ \frac{609y^2}{16} = 3 \]
\[ 609y^2 = 48 \]
\[ y^2 = \frac{48}{609} \]
\[ y = \sqrt{\frac{48}{609}} \approx 0.28 \]
Thay \( y = 0.28 \) vào \( x = \frac{25y}{4} \):
\[ x = \frac{25 \times 0.28}{4} = 1.75 \]
Vậy \( x = 1.75 \), \( y = 0.28 \).
Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh

 0
0



 0
0
 1
1
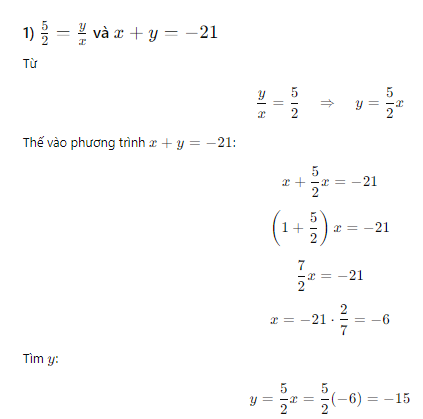
 0
0



