Cho đường tròn tâm O, bán kính R và đường thẳng d tiếp xúc với đường tròn (O) tại A. Lấy điểm M bất kì trên đường thẳng d (M khác A). Qua điểm M kẻ tiếp tuyến MB với đường tròn (B là tiếp điểm, B khác...

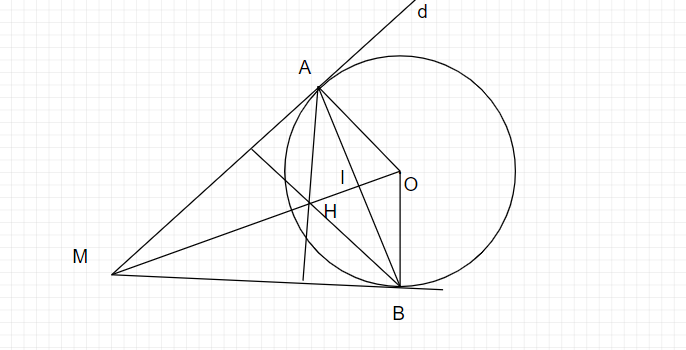
a/ Xét tứ giác OAMB có
$\displaystyle \widehat{MAO\ } +\ \widehat{MBO\ } =180^{0} \ $
Nên OAMB là tứ giác nội tiếp

b/ $\displaystyle \vartriangle MAO\ =\ \vartriangle MBO\ $ (cạnh huyền- cạnh góc vuông)
$\displaystyle \Rightarrow \widehat{BMO\ } \ =\ \widehat{AMO\ }$( hia góc tương ứng)
Mà $\displaystyle \widehat{OBA\ } \ =\widehat{OMA\ } \ $( OAMB là tứ giác nội tiếp)
$\displaystyle  \begin{array}{{>{\displaystyle}l}}
\Rightarrow \widehat{OBA\ } =\ \widehat{BMO\ } \ mà\ \ \widehat{BMO\ } +\widehat{MOB} =\ 90^{0\ }\\
Nên\ \ \widehat{OBA\ } +\ \widehat{MOB\ } =\ 90^{0} \ \\
Nên\ AB\ \perp \ OM\ tại\ I\ 
\end{array}$
xét tam giác AMO vuông tại A có AI là đường cao
$\displaystyle OI.OM\ =\ OA^{2} \ =\ R^{2} \ $

c/ $\displaystyle BH\ \perp AM;\ OA\ \perp AM\ $
$\displaystyle \Rightarrow BH//\ OA\ $ (1)
$\displaystyle AH\perp MB;\ OB\perp MB\ $
$\displaystyle \Rightarrow AH\ //\ OB\ $(2)
(1)(2)
Có AOBH là hình bình hành
xét hình bình hành AOBH có $\displaystyle AB\ \perp OH\ $
Nên AOBH là hình thoi 
Chu vi = 4.OA= 4R