25/02/2024
Cho tam giác MBC vuông tại M có góc B = 60° .
Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB . Chứng minh rằng tam giác ABC là tam giác đều .
Làm sao để có câu trả lời hay nhất?
- Luôn có GIẢI THÍCH các bước giải
- Không copy câu trả lời của Timi
- Không sao chép trên mạng
- Không spam câu trả lời để nhận điểm
- Spam sẽ bị khóa tài khoản



25/02/2024
 1
1
25/02/2024
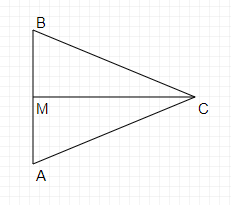
Ta có:
Lại có: M là trung điểm của AB (MA=MB)
MC vừa là đường cao, vừa là đường trung tuyến
Suy ra tam giác ABC cân tại C
Mà
Suy ra tam giác ABC đều.
 0
0
25/02/2024
Nguyễn Công ThuDo ∠MBC=60
∘
∠���=60∘
và ∠MBA=180
∘
−∠MBM
′
−∠MBM
′
=180
∘
−90
∘
−60
∘
=30
∘
∠���=180∘−∠���′−∠���′=180∘−90∘−60∘=30∘
(với M' là điểm đối xứng với M qua B).
Vậy ta có △MBA
△���
là tam giác vuông cân tại A (do MA=MB
��=��
), suy ra ∠MAB=∠MBA=45
∘
∠���=∠���=45∘
.
Do đó, ta có ∠ABC=∠ABM+∠MBC=45
∘
+60
∘
=105
∘
∠���=∠���+∠���=45∘+60∘=105∘
.
Tuy nhiên, trong tam giác ABC, ta có ∠BAC+∠ABC+∠BCA=180
∘
∠���+∠���+∠���=180∘
(tổng các góc trong một tam giác bằng 180
∘
180∘
).
Vậy nên, ∠BCA=180
∘
−∠BAC−∠ABC=180
∘
−45
∘
−105
∘
=30
∘
∠���=180∘−∠���−∠���=180∘−45∘−105∘=30∘
.
Như vậy, ta thấy rằng tam giác ABC là tam giác cân tại A (do BA=MA=MB
��=��=��
) và cân tại B (do BC=BM
��=��
), suy ra tam giác ABC là tam giác đều.
 0
0
25/02/2024
 1
1
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
21/04/2025
Top thành viên trả lời




 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác






