Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
có hai xã a b cùng ở một bên sông khoảng cách lần lượt là aa· =550m và bb·=600m khoảng cách a·b·=2200m cho một điểm m∈a·b· sao cho tổng khoáng cách hai xã đến m là nhỏ nhất
 0
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



04/11/2024
 0
0
04/11/2024
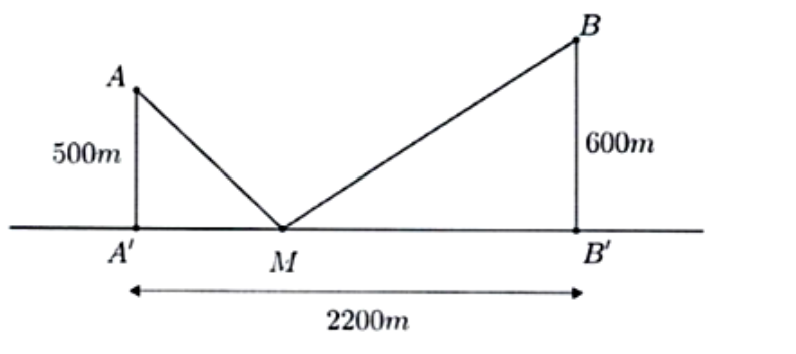
Đặt $AM = x (m)$.
Suy ra BM = AB' $-A M=2200-x(m)$.
Rõ ràng, x phải thỏa mãn điều kiện $0<x<2200$.
Áp dụng định lí Pythagore ta tính được:
$
\begin{aligned}
& \mathrm{AM}=\sqrt{A{A^{\prime}}^2+A^{\prime} M^2}=\sqrt{500^2+x^2}(\mathrm{~m}) \\
& \mathrm{BM}=\sqrt{B B^{\prime 2}+B^{\prime} M^2}=\sqrt{600^2+(2200-x)^2}(\mathrm{~m})
\end{aligned}
$
Tổng khoảng cách từ hai vị trí $\mathrm{A}, \mathrm{B}$ đến vị trí M là
$
\mathrm{D}=\mathrm{AM}+\mathrm{BM}=\sqrt{500^2+x^2}+\sqrt{600^2+(2200-x)^2}(\mathrm{~m}) .
$
Xét hàm số $\mathrm{D}(\mathrm{x})=\sqrt{500^2+x^2}+\sqrt{600^2+(2200-x)^2}$ với $\mathrm{x} \in(0 ; 2200)$.
Ta có $D^{\prime}(x)=\frac{x}{\sqrt{500^2+x^2}}+\frac{x-2200}{\sqrt{600^2+(2200-x)^2}}$;
Trên khoảng ( $0 ; 2200$ ), ta thấy $D^{\prime}(x)=0$ khi $x=1000$.
Bảng biến thiên của hàm số $D(x)$ như sau:
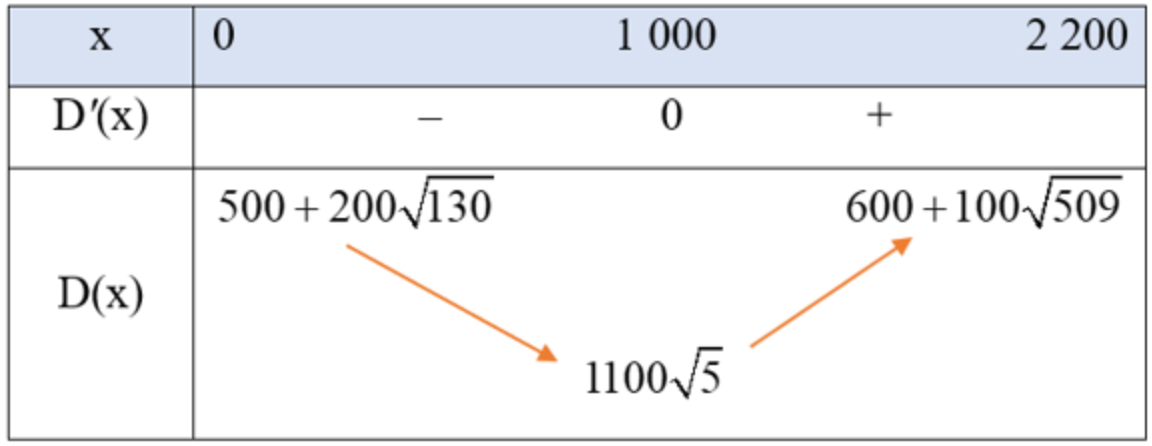
Căn cứ vào bảng biến thiên, ta thấy hàm số $D(x)$ đạt giá trị nhỏ nhất bằng $1100 \sqrt{5}$ tại $x=1000$. Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là $1100 \sqrt{5} \mathrm{~m}$.
 0
0
Nữa Gì
04/11/2024
huyhg1 aa- là 550m mà bạn ơi
04/11/2024
Nữa GìPhân tích và giải quyết
Bài toán này liên quan đến một định lý hình học quan trọng:
- Định lý: Trong một tam giác, tổng độ dài hai cạnh bất kỳ luôn lớn hơn độ dài cạnh còn lại.
Áp dụng vào bài toán:
- Giả sử: Điểm M không nằm giữa A và B.
- Xét tam giác AMB: Theo định lý trên, ta có: AM + MB > AB.
- Kết luận: Nếu M không nằm giữa A và B thì tổng khoảng cách AM + MB luôn lớn hơn AB.
Từ đó suy ra:
- Vị trí của M: Để tổng khoảng cách AM + MB nhỏ nhất, điểm M phải nằm giữa A và B.
- Giá trị nhỏ nhất của tổng khoảng cách: Giá trị nhỏ nhất của tổng khoảng cách AM + MB chính bằng độ dài đoạn thẳng AB, tức là 2200m.
 3
3
Nữa Gì
04/11/2024
Nguyễn hồng minh cảm ơn bạn
04/11/2024
Phân tích và giải quyết
Bài toán này liên quan đến một định lý hình học quan trọng:
- Định lý: Trong một tam giác, tổng độ dài hai cạnh bất kỳ luôn lớn hơn độ dài cạnh còn lại.
Áp dụng vào bài toán:
- Giả sử: Điểm M không nằm giữa A và B.
- Xét tam giác AMB: Theo định lý trên, ta có: AM + MB > AB.
- Kết luận: Nếu M không nằm giữa A và B thì tổng khoảng cách AM + MB luôn lớn hơn AB.
Từ đó suy ra:
- Vị trí của M: Để tổng khoảng cách AM + MB nhỏ nhất, điểm M phải nằm giữa A và B.
- Giá trị nhỏ nhất của tổng khoảng cách: Giá trị nhỏ nhất của tổng khoảng cách AM + MB chính bằng độ dài đoạn thẳng AB, tức là 2200m.
 2
2
Nữa Gì
04/11/2024
Lương Vũ cảm ơn bạn rất nhiều
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
8 giờ trước
Top thành viên trả lời



