Câu 10.
Để xác định hàm số có bảng biến thiên như trên, ta sẽ kiểm tra từng hàm số đã cho:
A. \( y = x^4 - 2x^2 \)
- Ta tính đạo hàm: \( y' = 4x^3 - 4x = 4x(x^2 - 1) = 4x(x - 1)(x + 1) \)
- Xét dấu đạo hàm:
- \( y' > 0 \) khi \( x < -1 \) hoặc \( 0 < x < 1 \)
- \( y' < 0 \) khi \( -1 < x < 0 \) hoặc \( x > 1 \)
- Vậy hàm số \( y = x^4 - 2x^2 \) tăng trên khoảng \( (-\infty, -1) \cup (0, 1) \) và giảm trên khoảng \( (-1, 0) \cup (1, +\infty) \).
B. \( y = -x^3 + 3x \)
- Ta tính đạo hàm: \( y' = -3x^2 + 3 = -3(x^2 - 1) = -3(x - 1)(x + 1) \)
- Xét dấu đạo hàm:
- \( y' > 0 \) khi \( -1 < x < 1 \)
- \( y' < 0 \) khi \( x < -1 \) hoặc \( x > 1 \)
- Vậy hàm số \( y = -x^3 + 3x \) tăng trên khoảng \( (-1, 1) \) và giảm trên khoảng \( (-\infty, -1) \cup (1, +\infty) \).
C. \( y = \frac{x - 2}{x + 3} \)
- Ta tính đạo hàm: \( y' = \frac{(x + 3) - (x - 2)}{(x + 3)^2} = \frac{5}{(x + 3)^2} \)
- Xét dấu đạo hàm:
- \( y' > 0 \) khi \( x \neq -3 \)
- Vậy hàm số \( y = \frac{x - 2}{x + 3} \) luôn tăng trên khoảng \( (-\infty, -3) \cup (-3, +\infty) \).
D. \( y = x^3 - 3x \)
- Ta tính đạo hàm: \( y' = 3x^2 - 3 = 3(x^2 - 1) = 3(x - 1)(x + 1) \)
- Xét dấu đạo hàm:
- \( y' > 0 \) khi \( x < -1 \) hoặc \( x > 1 \)
- \( y' < 0 \) khi \( -1 < x < 1 \)
- Vậy hàm số \( y = x^3 - 3x \) tăng trên khoảng \( (-\infty, -1) \cup (1, +\infty) \) và giảm trên khoảng \( (-1, 1) \).
So sánh với bảng biến thiên đã cho, ta thấy rằng hàm số \( y = x^3 - 3x \) có bảng biến thiên đúng như yêu cầu.
Vậy đáp án đúng là: D. \( y = x^3 - 3x \).
Câu 11.
Để tìm tọa độ hình chiếu vuông góc của điểm \( A(1;2;-1) \) lên mặt phẳng \( (Oyz) \), ta thực hiện các bước sau:
1. Xác định phương trình của mặt phẳng \( (Oyz) \):
Mặt phẳng \( (Oyz) \) có phương trình là \( x = 0 \).
2. Tìm tọa độ hình chiếu vuông góc:
- Hình chiếu vuông góc của điểm \( A(1;2;-1) \) lên mặt phẳng \( (Oyz) \) sẽ có tọa độ \( (0; y; z) \).
- Vì hình chiếu vuông góc giữ nguyên các tọa độ \( y \) và \( z \) của điểm \( A \), nên ta có \( y = 2 \) và \( z = -1 \).
Do đó, tọa độ hình chiếu vuông góc của điểm \( A \) lên mặt phẳng \( (Oyz) \) là \( (0; 2; -1) \).
Vậy đáp án đúng là:
A. \( (0; 2; -1) \).
Câu 12.
Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( f(x) = x^4 - 2x^2 - 1 \) trên đoạn \([-1; 2]\), ta thực hiện các bước sau:
Bước 1: Tính đạo hàm của hàm số.
\[ f'(x) = 4x^3 - 4x \]
Bước 2: Tìm các điểm cực trị bằng cách giải phương trình đạo hàm bằng 0.
\[ f'(x) = 0 \]
\[ 4x^3 - 4x = 0 \]
\[ 4x(x^2 - 1) = 0 \]
\[ x = 0 \quad \text{hoặc} \quad x^2 - 1 = 0 \]
\[ x = 0 \quad \text{hoặc} \quad x = \pm 1 \]
Bước 3: Kiểm tra các giá trị của hàm số tại các điểm cực trị và tại các biên của đoạn \([-1; 2]\).
\[ f(-1) = (-1)^4 - 2(-1)^2 - 1 = 1 - 2 - 1 = -2 \]
\[ f(0) = 0^4 - 2 \cdot 0^2 - 1 = -1 \]
\[ f(1) = 1^4 - 2 \cdot 1^2 - 1 = 1 - 2 - 1 = -2 \]
\[ f(2) = 2^4 - 2 \cdot 2^2 - 1 = 16 - 8 - 1 = 7 \]
Bước 4: So sánh các giá trị để xác định giá trị lớn nhất và giá trị nhỏ nhất.
\[ f(-1) = -2 \]
\[ f(0) = -1 \]
\[ f(1) = -2 \]
\[ f(2) = 7 \]
Từ đó, ta thấy:
- Giá trị lớn nhất \( M = 7 \)
- Giá trị nhỏ nhất \( m = -2 \)
Bước 5: Tính giá trị của biểu thức \( M + 3m \).
\[ M + 3m = 7 + 3(-2) = 7 - 6 = 1 \]
Vậy giá trị của biểu thức \( M + 3m \) là 1.
Đáp án đúng là: A. 1.
Câu 13.
Để tìm tọa độ của véctơ $\overrightarrow{AB}$, ta sử dụng công thức tính hiệu của hai véctơ trong không gian. Cụ thể, nếu $\overrightarrow{OA} = (x_1, y_1, z_1)$ và $\overrightarrow{OB} = (x_2, y_2, z_2)$, thì tọa độ của véctơ $\overrightarrow{AB}$ sẽ là:
\[
\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = (x_2 - x_1, y_2 - y_1, z_2 - z_1)
\]
Áp dụng vào bài toán này, ta có:
\[
\overrightarrow{OA} = (2, -1, 3)
\]
\[
\overrightarrow{OB} = (5, 2, -1)
\]
Tính hiệu của hai véctơ:
\[
\overrightarrow{AB} = (5 - 2, 2 - (-1), -1 - 3) = (3, 3, -4)
\]
Vậy tọa độ của véctơ $\overrightarrow{AB}$ là $(3, 3, -4)$.
Do đó, đáp án đúng là:
B. $(3, 3, -4)$.
Câu 14.
Để tìm tọa độ điểm \( M \) thỏa mãn \(\overrightarrow{AB} = 2\overrightarrow{MA}\), ta thực hiện các bước sau:
1. Tìm tọa độ của vectơ \(\overrightarrow{AB}\):
\[
\overrightarrow{AB} = B - A = (1 - (-1); 0 - 2; 2 - 3) = (2; -2; -1)
\]
2. Gọi tọa độ của điểm \( M \) là \( M(x; y; z) \).
Tọa độ của vectơ \(\overrightarrow{MA}\) sẽ là:
\[
\overrightarrow{MA} = A - M = (-1 - x; 2 - y; 3 - z)
\]
3. Áp dụng điều kiện \(\overrightarrow{AB} = 2\overrightarrow{MA}\):
\[
(2; -2; -1) = 2(-1 - x; 2 - y; 3 - z)
\]
Ta có hệ phương trình:
\[
\begin{cases}
2 = 2(-1 - x) \\
-2 = 2(2 - y) \\
-1 = 2(3 - z)
\end{cases}
\]
4. Giải hệ phương trình:
\[
\begin{cases}
2 = -2 - 2x \implies 2 + 2 = -2x \implies 4 = -2x \implies x = -2 \\
-2 = 4 - 2y \implies -2 - 4 = -2y \implies -6 = -2y \implies y = 3 \\
-1 = 6 - 2z \implies -1 - 6 = -2z \implies -7 = -2z \implies z = \frac{7}{2}
\end{cases}
\]
5. Tọa độ của điểm \( M \) là:
\[
M(-2; 3; \frac{7}{2})
\]
Vậy đáp án đúng là:
A. \( M(-2; 3; \frac{7}{2}) \)
Câu 15.
Để xác định hàm số có đồ thị như hình vẽ, ta sẽ kiểm tra từng hàm số đã cho để xem chúng có thỏa mãn các đặc điểm của đồ thị hay không.
1. Kiểm tra giới hạn khi \( x \to \pm \infty \):
- Đồ thị có hai đường tiệm cận đứng và tiệm cận ngang, do đó hàm số phải là một hàm phân thức.
- Giới hạn khi \( x \to \pm \infty \) của hàm số phải là một hằng số, cụ thể là \( y = 1 \) hoặc \( y = -1 \).
2. Kiểm tra các hàm số:
- A. \( y = \frac{x}{x + 1} \)
- Khi \( x \to \infty \), \( y \to 1 \).
- Khi \( x \to -\infty \), \( y \to 1 \).
- Tiệm cận đứng là \( x = -1 \).
- Không thỏa mãn vì đồ thị không có tiệm cận ngang là \( y = -1 \).
- B. \( y = -\frac{x}{x - 1} \)
- Khi \( x \to \infty \), \( y \to -1 \).
- Khi \( x \to -\infty \), \( y \to -1 \).
- Tiệm cận đứng là \( x = 1 \).
- Thỏa mãn vì đồ thị có tiệm cận ngang là \( y = -1 \) và tiệm cận đứng là \( x = 1 \).
- C. \( y = -\frac{x}{x + 1} \)
- Khi \( x \to \infty \), \( y \to -1 \).
- Khi \( x \to -\infty \), \( y \to -1 \).
- Tiệm cận đứng là \( x = -1 \).
- Không thỏa mãn vì đồ thị không có tiệm cận ngang là \( y = 1 \).
- D. \( y = \frac{x}{x - 1} \)
- Khi \( x \to \infty \), \( y \to 1 \).
- Khi \( x \to -\infty \), \( y \to 1 \).
- Tiệm cận đứng là \( x = 1 \).
- Không thỏa mãn vì đồ thị không có tiệm cận ngang là \( y = -1 \).
Từ các phân tích trên, chỉ có hàm số \( y = -\frac{x}{x - 1} \) thỏa mãn tất cả các đặc điểm của đồ thị.
Đáp án: B. \( y = -\frac{x}{x - 1} \)
Câu 17.
Để tìm tọa độ trung điểm \(M\) của đoạn thẳng \(BC\), ta cần biết tọa độ của \(B\) và \(C\). Tuy nhiên, bài toán chỉ cung cấp tọa độ của điểm \(A\) và tổng của hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\).
Ta có:
\[ \overrightarrow{AB} + \overrightarrow{AC} = (4, 0, -6) \]
Gọi \(B(x_1, y_1, z_1)\) và \(C(x_2, y_2, z_2)\). Ta có:
\[ \overrightarrow{AB} = (x_1 - 1, y_1 - 1, z_1 - 1) \]
\[ \overrightarrow{AC} = (x_2 - 1, y_2 - 1, z_2 - 1) \]
Do đó:
\[ \overrightarrow{AB} + \overrightarrow{AC} = ((x_1 - 1) + (x_2 - 1), (y_1 - 1) + (y_2 - 1), (z_1 - 1) + (z_2 - 1)) \]
\[ = (x_1 + x_2 - 2, y_1 + y_2 - 2, z_1 + z_2 - 2) \]
Theo đề bài:
\[ (x_1 + x_2 - 2, y_1 + y_2 - 2, z_1 + z_2 - 2) = (4, 0, -6) \]
Từ đây, ta có hệ phương trình:
\[ x_1 + x_2 - 2 = 4 \]
\[ y_1 + y_2 - 2 = 0 \]
\[ z_1 + z_2 - 2 = -6 \]
Giải hệ phương trình này:
\[ x_1 + x_2 = 6 \]
\[ y_1 + y_2 = 2 \]
\[ z_1 + z_2 = -4 \]
Trung điểm \(M\) của đoạn thẳng \(BC\) có tọa độ:
\[ M \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2} \right) \]
Thay vào:
\[ M \left( \frac{6}{2}, \frac{2}{2}, \frac{-4}{2} \right) = (3, 1, -2) \]
Vậy tọa độ trung điểm \(M\) của đoạn thẳng \(BC\) là:
\[ \boxed{(3, 1, -2)} \]
Câu 18.
Trước tiên, ta xét tính chất của hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong hình bình hành, ta có các tính chất sau:
1. Các cặp cạnh đối song song và bằng nhau.
2. Các đường chéo cắt nhau tại trung điểm.
Bây giờ, ta sẽ kiểm tra từng đẳng thức đã cho:
A. $\overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC} + \overrightarrow{SD} = \overrightarrow{0}$.
Để kiểm tra đẳng thức này, ta cần xem xét tổng của các vectơ từ đỉnh S đến các đỉnh của đáy. Ta thấy rằng, trong hình chóp S.ABCD, các vectơ $\overrightarrow{SA}$, $\overrightarrow{SB}$, $\overrightarrow{SC}$, và $\overrightarrow{SD}$ không phải lúc nào cũng tạo thành một tổng bằng vectơ null. Do đó, đẳng thức này không phải lúc nào cũng đúng.
B. $\overrightarrow{SA} + \overrightarrow{SC} = \overrightarrow{SB} + \overrightarrow{SD}$.
Ta xét tổng của các vectơ từ đỉnh S đến các đỉnh A và C, và so sánh với tổng của các vectơ từ đỉnh S đến các đỉnh B và D. Ta thấy rằng, do tính chất của hình bình hành, ta có:
$\overrightarrow{AC} = \overrightarrow{BD}$
Do đó, ta có:
$\overrightarrow{SA} + \overrightarrow{SC} = \overrightarrow{SA} + (\overrightarrow{SB} + \overrightarrow{BD}) = \overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{BD}$
và
$\overrightarrow{SB} + \overrightarrow{SD} = \overrightarrow{SB} + (\overrightarrow{SA} + \overrightarrow{AC}) = \overrightarrow{SB} + \overrightarrow{SA} + \overrightarrow{AC}$
Vì $\overrightarrow{AC} = \overrightarrow{BD}$, nên ta có:
$\overrightarrow{SA} + \overrightarrow{SC} = \overrightarrow{SB} + \overrightarrow{SD}$
Do đó, đẳng thức này là đúng.
C. $\overrightarrow{SA} + \overrightarrow{SB} = \overrightarrow{SC} + \overrightarrow{SD}$.
Ta xét tổng của các vectơ từ đỉnh S đến các đỉnh A và B, và so sánh với tổng của các vectơ từ đỉnh S đến các đỉnh C và D. Ta thấy rằng, do tính chất của hình bình hành, ta có:
$\overrightarrow{AB} = \overrightarrow{DC}$
Do đó, ta có:
$\overrightarrow{SA} + \overrightarrow{SB} = \overrightarrow{SA} + (\overrightarrow{SC} + \overrightarrow{CB}) = \overrightarrow{SA} + \overrightarrow{SC} + \overrightarrow{CB}$
và
$\overrightarrow{SC} + \overrightarrow{SD} = \overrightarrow{SC} + (\overrightarrow{SA} + \overrightarrow{AD}) = \overrightarrow{SC} + \overrightarrow{SA} + \overrightarrow{AD}$
Vì $\overrightarrow{CB} = \overrightarrow{AD}$, nên ta có:
$\overrightarrow{SA} + \overrightarrow{SB} = \overrightarrow{SC} + \overrightarrow{SD}$
Do đó, đẳng thức này là đúng.
D. $\overrightarrow{SB} + \overrightarrow{SC} = \overrightarrow{SA} + \overrightarrow{SD}$.
Ta xét tổng của các vectơ từ đỉnh S đến các đỉnh B và C, và so sánh với tổng của các vectơ từ đỉnh S đến các đỉnh A và D. Ta thấy rằng, do tính chất của hình bình hành, ta có:
$\overrightarrow{BC} = \overrightarrow{AD}$
Do đó, ta có:
$\overrightarrow{SB} + \overrightarrow{SC} = \overrightarrow{SB} + (\overrightarrow{SA} + \overrightarrow{AC}) = \overrightarrow{SB} + \overrightarrow{SA} + \overrightarrow{AC}$
và
$\overrightarrow{SA} + \overrightarrow{SD} = \overrightarrow{SA} + (\overrightarrow{SB} + \overrightarrow{BD}) = \overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{BD}$
Vì $\overrightarrow{AC} = \overrightarrow{BD}$, nên ta có:
$\overrightarrow{SB} + \overrightarrow{SC} = \overrightarrow{SA} + \overrightarrow{SD}$
Do đó, đẳng thức này là đúng.
Tóm lại, các đẳng thức đúng là:
B. $\overrightarrow{SA} + \overrightarrow{SC} = \overrightarrow{SB} + \overrightarrow{SD}$.
C. $\overrightarrow{SA} + \overrightarrow{SB} = \overrightarrow{SC} + \overrightarrow{SD}$.
D. $\overrightarrow{SB} + \overrightarrow{SC} = \overrightarrow{SA} + \overrightarrow{SD}$.
Đáp án: B, C, D.
Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh

 0
0



 0
0
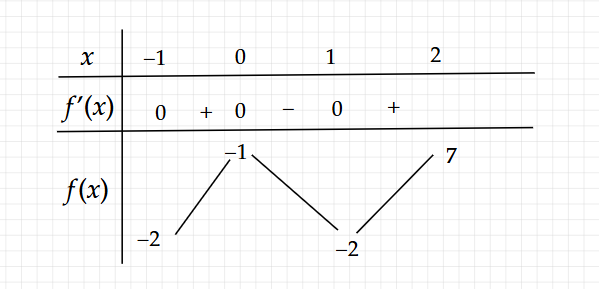
 0
0
 0
0



