Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
giúp mình với

 0
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



08/11/2024
 0
0
08/11/2024
Câu 10:
Giả sử chiều dài từng mặt của ba mặt hàng rào song song nhau là x (m).
Chi phí để làm ba mặt hàng rào song song là: 3 ∙ x ∙ 50 000 = 150 000x (đồng).
Chi phí để làm mặt hàng rào song song với bờ sông là: 15 000 000 – 150 000x (đồng).
Chiều dài của mặt hàng rào song song với bờ sông là
(m).
Rõ ràng, x phải thỏa mãn điều kiện 0 < x < 100.
Giả sử diện tích hàng rào không đáng kể, khi đó diện tích hai khu đất thu được sau khi làm hàng rào là S(x) = (m2).
Xét hàm số với x ∈ (0; 100).
Ta có S'(x) = .
Trên khoảng (0; 100), S'(x) = 0 khi x = 50.
Bảng biến thiên của hàm số S(x) như sau:
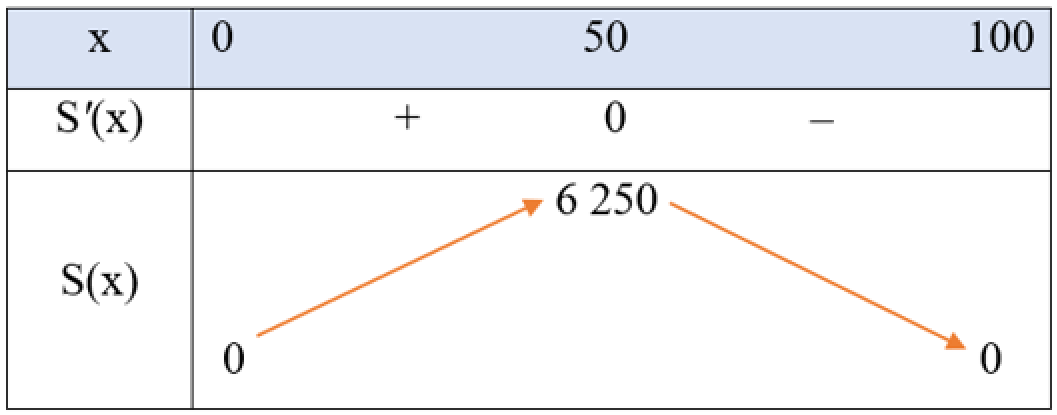
Căn cứ bảng biến thiên, ta thấy: Trên khoảng (0; 100), hàm số S(x) đạt giá trị lớn nhất bằng 6 250 tại x = 50.
Vậy diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào là 6 250 m2.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
9 giờ trước
11 giờ trước
11 giờ trước
19/12/2025
Top thành viên trả lời



