giup e voi a

Câu 3. Quy tắc ba điểm: Cho hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$. Ta có: \[ \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC} \] Hình vẽ minh họa: A |\ | \ | \ B---C Quy tắc hình bình hành: Cho hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AD}$. Ta có: \[ \overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC} \] Hình vẽ minh họa: A----D |\ | | \ | | \ | B----C Quy tắc hình hộp: Cho ba vectơ $\overrightarrow{AB}$, $\overrightarrow{AD}$ và $\overrightarrow{AE}$. Ta có: \[ \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AE} = \overrightarrow{AF} \] Hình vẽ minh họa: A----D----H |\ |\ | | \ | \ | | \ | \ | B----E----F | /| / | / | / | / | / C----G Quy tắc trừ: Cho hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$. Ta có: \[ \overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB} \] Hình vẽ minh họa: A |\ | \ | \ B---C Trên đây là các quy tắc về vectơ đã được nêu chi tiết và minh họa bằng hình vẽ. Câu 4. a. Chứng minh A, B, C là ba đỉnh của một tam giác: - Tính khoảng cách giữa các điểm: - \( AB = \sqrt{(2 - (-1))^2 + (1 - 0)^2 + (-1 - 3)^2} = \sqrt{3^2 + 1^2 + (-4)^2} = \sqrt{9 + 1 + 16} = \sqrt{26} \) - \( BC = \sqrt{(3 - 2)^2 + (2 - 1)^2 + (2 - (-1))^2} = \sqrt{1^2 + 1^2 + 3^2} = \sqrt{1 + 1 + 9} = \sqrt{11} \) - \( CA = \sqrt{(3 - (-1))^2 + (2 - 0)^2 + (2 - 3)^2} = \sqrt{4^2 + 2^2 + (-1)^2} = \sqrt{16 + 4 + 1} = \sqrt{21} \) - Kiểm tra điều kiện tam giác: - \( AB + BC > CA \): \( \sqrt{26} + \sqrt{11} > \sqrt{21} \) (đúng) - \( AB + CA > BC \): \( \sqrt{26} + \sqrt{21} > \sqrt{11} \) (đúng) - \( BC + CA > AB \): \( \sqrt{11} + \sqrt{21} > \sqrt{26} \) (đúng) Vậy A, B, C là ba đỉnh của một tam giác. b. Tìm tọa độ đỉnh D để tứ giác ABCD là hình bình hành: - Trung điểm của AC: \( M = \left( \frac{-1 + 3}{2}, \frac{0 + 2}{2}, \frac{3 + 2}{2} \right) = (1, 1, 2.5) \) - Trung điểm của BD cũng phải là M, vậy: - \( \left( \frac{2 + x_D}{2}, \frac{1 + y_D}{2}, \frac{-1 + z_D}{2} \right) = (1, 1, 2.5) \) - \( \frac{2 + x_D}{2} = 1 \Rightarrow x_D = 0 \) - \( \frac{1 + y_D}{2} = 1 \Rightarrow y_D = 1 \) - \( \frac{-1 + z_D}{2} = 2.5 \Rightarrow z_D = 6 \) Vậy tọa độ đỉnh D là \( D(0, 1, 6) \). c. Tìm tọa độ trung điểm của AD: - Trung điểm của AD: \( N = \left( \frac{-1 + 0}{2}, \frac{0 + 1}{2}, \frac{3 + 6}{2} \right) = \left( -\frac{1}{2}, \frac{1}{2}, \frac{9}{2} \right) \) d. Tìm tọa độ trọng tâm của tam giác BCD: - Trọng tâm của tam giác BCD: \( G = \left( \frac{2 + 3 + 0}{3}, \frac{1 + 2 + 1}{3}, \frac{-1 + 2 + 6}{3} \right) = \left( \frac{5}{3}, \frac{4}{3}, \frac{7}{3} \right) \) Đáp số: a. A, B, C là ba đỉnh của một tam giác. b. Tọa độ đỉnh D: \( D(0, 1, 6) \) c. Tọa độ trung điểm của AD: \( \left( -\frac{1}{2}, \frac{1}{2}, \frac{9}{2} \right) \) d. Tọa độ trọng tâm của tam giác BCD: \( \left( \frac{5}{3}, \frac{4}{3}, \frac{7}{3} \right) \) Câu 5. 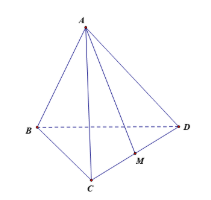Trước tiên, ta xác định các điểm và véc tơ liên quan: - Tứ diện đều ABCD có độ dài cạnh bằng 2. - M là trung điểm của CD. Ta cần tính tích vô hướng của hai véc tơ $\overrightarrow{AB}$ và $\overrightarrow{AM}$. Bước 1: Xác định tọa độ các đỉnh của tứ diện đều ABCD. Giả sử: - A(0, 0, 0) - B(2, 0, 0) - C(1, $\sqrt{3}$, 0) - D(1, $\frac{\sqrt{3}}{3}$, $\sqrt{\frac{8}{3}}$) Bước 2: Tìm tọa độ của điểm M. M là trung điểm của CD, nên tọa độ của M là: \[ M\left(\frac{1+1}{2}, \frac{\sqrt{3} + \frac{\sqrt{3}}{3}}{2}, \frac{0 + \sqrt{\frac{8}{3}}}{2}\right) = M\left(1, \frac{2\sqrt{3}}{3}, \frac{\sqrt{\frac{8}{3}}}{2}\right) = M\left(1, \frac{2\sqrt{3}}{3}, \frac{\sqrt{8}}{3}\right) = M\left(1, \frac{2\sqrt{3}}{3}, \frac{2\sqrt{2}}{3}\right) \] Bước 3: Xác định các véc tơ $\overrightarrow{AB}$ và $\overrightarrow{AM}$. \[ \overrightarrow{AB} = B - A = (2, 0, 0) - (0, 0, 0) = (2, 0, 0) \] \[ \overrightarrow{AM} = M - A = \left(1, \frac{2\sqrt{3}}{3}, \frac{2\sqrt{2}}{3}\right) - (0, 0, 0) = \left(1, \frac{2\sqrt{3}}{3}, \frac{2\sqrt{2}}{3}\right) \] Bước 4: Tính tích vô hướng của hai véc tơ $\overrightarrow{AB}$ và $\overrightarrow{AM}$. \[ \overrightarrow{AB} \cdot \overrightarrow{AM} = (2, 0, 0) \cdot \left(1, \frac{2\sqrt{3}}{3}, \frac{2\sqrt{2}}{3}\right) = 2 \times 1 + 0 \times \frac{2\sqrt{3}}{3} + 0 \times \frac{2\sqrt{2}}{3} = 2 \] Vậy, tích vô hướng của hai véc tơ $\overrightarrow{AB}$ và $\overrightarrow{AM}$ là 2.