Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
Giúp mình với!

 0
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



21/12/2024
 0
0
21/12/2024
Bài 4:
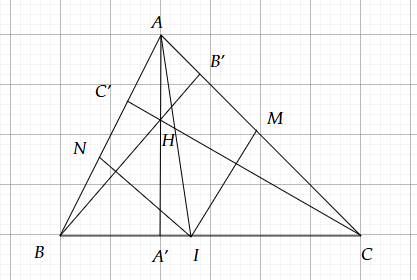
a)
Có: $\displaystyle \frac{S_{HBC}}{S_{ABC}} =\frac{\frac{1}{2} .HA'.BC}{\frac{1}{2} .AA'.BC} =\frac{HA'}{AA'}$
$\displaystyle \frac{S_{HAB}}{S_{ABC}} =\frac{\frac{1}{2} .HC'.AB}{\frac{1}{2} .CC'.AB} =\frac{HC'}{CC'}$
$\displaystyle \frac{S_{HAC}}{S_{ABC}} =\frac{\frac{1}{2} .HB'.AC}{\frac{1}{2} .BB'.AC} =\frac{HB'}{BB'}$
$\displaystyle \Longrightarrow \frac{HA'}{AA'} +\frac{HB'}{BB'} +\frac{HC'}{CC'} =\frac{S_{HBC}}{S_{ABC}} +\frac{S_{HAB}}{S_{ABC}} +\frac{S_{HAC}}{S_{ABC}} =\frac{S_{ABC}}{S_{ABC}} =$
b)
Áp dụng tính chất phân giác vào tam giác ABC, AIB, AIC. có:
$\displaystyle \frac{IB}{IC} =\frac{AB}{AC}$
$\displaystyle \frac{AN}{NB} =\frac{IA}{IB}$
$\displaystyle \frac{CM}{MA} =\frac{IC}{IA}$
$\displaystyle \begin{array}{{>{\displaystyle}l}}
\Longrightarrow \frac{IB}{IC} .\frac{AN}{NB} .\frac{CM}{MA} =\frac{AB}{AC} .\frac{IA}{IB} .\frac{IC}{IA} =\frac{AB}{AC} .\frac{IC}{IB} =1\\
\Longrightarrow AN.BI.CM=BN.IC.AM
\end{array}$
 0
0
21/12/2024
a) Tứ giác AMNI là hình gì? Chứng minh?
- Phân tích:Ta có: M, N lần lượt là trung điểm của BD, BC.
- BD là phân giác góc ABC.
- Từ đó, ta sẽ chứng minh tứ giác AMNI là hình chữ nhật.
- Chứng minh:Xét tam giác BCD có:
- M là trung điểm BD
- N là trung điểm BC => MN là đường trung bình của tam giác BCD. => MN // CD và MN = 1/2 CD.
- Tương tự, ta chứng minh được MI // AB và MI = 1/2 AB.
- Mà AB vuông góc với CD (do tam giác ABC vuông tại A) => MN vuông góc với MI.
- Tứ giác AMNI có 3 góc vuông (góc A, góc M, góc N) nên là hình chữ nhật.
b) Cho AB = 4cm. Tính các cạnh của tứ giác AMNI
- Giải:Ta đã chứng minh được AMNI là hình chữ nhật.
- MI = 1/2 AB = 1/2 * 4 = 2cm.
- MN = 1/2 CD. Để tính CD, ta cần thêm thông tin về độ dài các cạnh khác của tam giác ABC.
Bài 4:
a) Tính tổng HA/AA' + HB/BB' + HC/CC'
- Phân tích:Đây là một bài toán kinh điển về đường cao trong tam giác.
- Ta sẽ sử dụng các hệ thức lượng trong tam giác vuông để giải quyết bài toán.
- Chứng minh:Sử dụng định lý Euler: Trong tam giác ABC, ta có: 1/AA'^2 + 1/BB'^2 + 1/CC'^2 = 1/r^2
- Đảo ngược cả hai vế, ta được: HA/AA' + HB/BB' + HC/CC' = r^2 Trong đó, r là bán kính đường tròn nội tiếp tam giác ABC.
b) Gọi AI là phân giác của tam giác ABC. Gọi IM, IN thứ tự là phân giác của góc AIC và AIB. Chứng minh rằng AN.BI.CM = BN.IC.AM
- Phân tích:Đây là bài toán về tính chất đường phân giác trong tam giác.
- Ta sẽ sử dụng định lý Stewart và tính chất đường phân giác để chứng minh.
- Chứng minh:Áp dụng định lý Stewart cho tam giác ABI với phân giác IM, ta có: BI^2.AM + AI^2.BM = AB.IM^2 + AI.BM.IM
- Tương tự, áp dụng định lý Stewart cho tam giác ACI với phân giác IN, ta có: CI^2.AN + AI^2.CN = AC.IN^2 + AI.CN.IN
- Chia vế theo vế hai đẳng thức trên, sau đó rút gọn và biến đổi, ta được: AN.BI.CM = BN.IC.AM
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
2 giờ trước
Top thành viên trả lời



