giải hộ mình với

Câu 17. Để tính xác suất của biến cố "Tổng số chấm xuất hiện trên 3 con xúc xắc nhỏ hơn 15", chúng ta sẽ thực hiện các bước sau: 1. Xác định không gian mẫu: Mỗi con xúc xắc có 6 mặt, do đó khi gieo 3 con xúc xắc, tổng số kết quả có thể xảy ra là: \[ 6 \times 6 \times 6 = 216 \] 2. Xác định số trường hợp thuận lợi: Chúng ta cần tìm số trường hợp mà tổng số chấm xuất hiện trên 3 con xúc xắc nhỏ hơn 15. Để làm điều này, chúng ta sẽ liệt kê tất cả các trường hợp có tổng nhỏ hơn 15. Các trường hợp có tổng nhỏ hơn 15 bao gồm: - Tổng = 3: (1, 1, 1) - Tổng = 4: (1, 1, 2), (1, 2, 1), (2, 1, 1) - Tổng = 5: (1, 1, 3), (1, 3, 1), (3, 1, 1), (1, 2, 2), (2, 1, 2), (2, 2, 1) - Tổng = 6: (1, 1, 4), (1, 4, 1), (4, 1, 1), (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1), (2, 2, 2) - Tổng = 7: (1, 1, 5), (1, 5, 1), (5, 1, 1), (1, 2, 4), (1, 4, 2), (2, 1, 4), (2, 4, 1), (4, 1, 2), (4, 2, 1), (1, 3, 3), (3, 1, 3), (3, 3, 1), (2, 2, 3), (2, 3, 2), (3, 2, 2) - Tổng = 8: (1, 1, 6), (1, 6, 1), (6, 1, 1), (1, 2, 5), (1, 5, 2), (2, 1, 5), (2, 5, 1), (5, 1, 2), (5, 2, 1), (1, 3, 4), (1, 4, 3), (3, 1, 4), (3, 4, 1), (4, 1, 3), (4, 3, 1), (2, 2, 4), (2, 4, 2), (4, 2, 2), (2, 3, 3), (3, 2, 3), (3, 3, 2) - Tổng = 9: (1, 2, 6), (1, 6, 2), (2, 1, 6), (2, 6, 1), (6, 1, 2), (6, 2, 1), (1, 3, 5), (1, 5, 3), (3, 1, 5), (3, 5, 1), (5, 1, 3), (5, 3, 1), (1, 4, 4), (4, 1, 4), (4, 4, 1), (2, 2, 5), (2, 5, 2), (5, 2, 2), (2, 3, 4), (2, 4, 3), (3, 2, 4), (3, 4, 2), (4, 2, 3), (4, 3, 2), (3, 3, 3) - Tổng = 10: (1, 3, 6), (1, 6, 3), (3, 1, 6), (3, 6, 1), (6, 1, 3), (6, 3, 1), (1, 4, 5), (1, 5, 4), (4, 1, 5), (4, 5, 1), (5, 1, 4), (5, 4, 1), (2, 2, 6), (2, 6, 2), (6, 2, 2), (2, 3, 5), (2, 5, 3), (3, 2, 5), (3, 5, 2), (5, 2, 3), (5, 3, 2), (2, 4, 4), (4, 2, 4), (4, 4, 2), (3, 3, 4), (3, 4, 3), (4, 3, 3) - Tổng = 11: (1, 4, 6), (1, 6, 4), (4, 1, 6), (4, 6, 1), (6, 1, 4), (6, 4, 1), (1, 5, 5), (5, 1, 5), (5, 5, 1), (2, 3, 6), (2, 6, 3), (3, 2, 6), (3, 6, 2), (6, 2, 3), (6, 3, 2), (2, 4, 5), (2, 5, 4), (4, 2, 5), (4, 5, 2), (5, 2, 4), (5, 4, 2), (3, 3, 5), (3, 5, 3), (5, 3, 3), (3, 4, 4), (4, 3, 4), (4, 4, 3) - Tổng = 12: (1, 5, 6), (1, 6, 5), (5, 1, 6), (5, 6, 1), (6, 1, 5), (6, 5, 1), (2, 4, 6), (2, 6, 4), (4, 2, 6), (4, 6, 2), (6, 2, 4), (6, 4, 2), (2, 5, 5), (5, 2, 5), (5, 5, 2), (3, 3, 6), (3, 6, 3), (6, 3, 3), (3, 4, 5), (3, 5, 4), (4, 3, 5), (4, 5, 3), (5, 3, 4), (5, 4, 3), (4, 4, 4) - Tổng = 13: (1, 6, 6), (6, 1, 6), (6, 6, 1), (2, 5, 6), (2, 6, 5), (5, 2, 6), (5, 6, 2), (6, 2, 5), (6, 5, 2), (3, 4, 6), (3, 6, 4), (4, 3, 6), (4, 6, 3), (6, 3, 4), (6, 4, 3), (3, 5, 5), (5, 3, 5), (5, 5, 3), (4, 4, 5), (4, 5, 4), (5, 4, 4) - Tổng = 14: (2, 6, 6), (6, 2, 6), (6, 6, 2), (3, 5, 6), (3, 6, 5), (5, 3, 6), (5, 6, 3), (6, 3, 5), (6, 5, 3), (4, 4, 6), (4, 6, 4), (6, 4, 4), (4, 5, 5), (5, 4, 5), (5, 5, 4) Tổng cộng có 100 trường hợp thuận lợi. 3. Tính xác suất: Xác suất của biến cố "Tổng số chấm xuất hiện trên 3 con xúc xắc nhỏ hơn 15" là: \[ P = \frac{\text{số trường hợp thuận lợi}}{\text{số trường hợp có thể xảy ra}} = \frac{100}{216} \approx 0.46 \] Vậy xác suất của biến cố "Tổng số chấm xuất hiện trên 3 con xúc xắc nhỏ hơn 15" là khoảng 0.46. Câu 18. Điều kiện xác định: $m < \frac{17}{4}$. Theo định lý Viet ta có: $x_1 + x_2 = 5$ $x_1.x_2 = m + 2$ Ta có: $P = x^2_1x_2 + x_1x^2_2 - x^2_1x^2_2 - 4$ $= x_1x_2(x_1 + x_2) - x^2_1x^2_2 - 4$ $= 5(m + 2) - (m + 2)^2 - 4$ $= - m^2 + m + 6$ $= -(m - \frac{1}{2})^2 + \frac{25}{4}$ Vì $m < \frac{17}{4}$ nên P đạt giá trị lớn nhất bằng $\frac{25}{4}$ khi $m = \frac{1}{2}$. Vậy giá trị của m để biểu thức $P = x^2_1x_2 + x_1x^2_2 - x^2_1x^2_2 - 4$ đạt giá trị lớn nhất là $\frac{25}{4}$ là $m = \frac{1}{2}$. Câu 19. Để giải bài toán này, chúng ta sẽ sử dụng công thức liên quan đến bán kính đường tròn nội tiếp của tam giác đều. Bước 1: Xác định công thức liên quan Bán kính đường tròn nội tiếp của tam giác đều (r) được tính theo công thức: \[ r = \frac{a \sqrt{3}}{6} \] Trong đó, \( a \) là độ dài cạnh của tam giác đều. Bước 2: Thay giá trị vào công thức Biết rằng bán kính đường tròn nội tiếp (r) là 4 dm, ta thay vào công thức: \[ 4 = \frac{a \sqrt{3}}{6} \] Bước 3: Giải phương trình để tìm độ dài cạnh \( a \) Nhân cả hai vế với 6: \[ 24 = a \sqrt{3} \] Chia cả hai vế cho \( \sqrt{3} \): \[ a = \frac{24}{\sqrt{3}} \] Rationalize mẫu số: \[ a = \frac{24 \sqrt{3}}{3} = 8 \sqrt{3} \] Bước 4: Tính giá trị số học của \( a \) \[ a = 8 \sqrt{3} \approx 8 \times 1.732 = 13.856 \text{ dm} \] Vậy khoảng cách giữa hai vị trí A và B là khoảng cách giữa hai đỉnh của tam giác đều, tức là độ dài cạnh của tam giác đều. Đáp số: Khoảng cách giữa hai vị trí A và B là 13.86 dm (làm tròn đến hàng phần trăm). Câu 20. 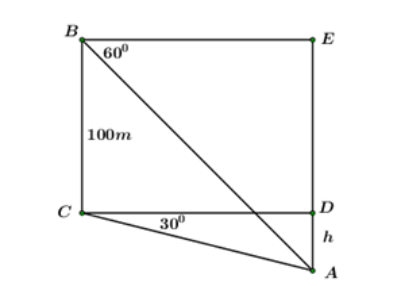Trước tiên, ta cần vẽ lại hình vẽ để dễ dàng quan sát và giải bài toán. Ta có góc BAC = 60° và góc CAB = 30°. Do đó, tam giác ABC là tam giác vuông cân tại A. Chiều cao của quả đồi là h, chiều cao của tháp là 100m. Ta có: tan(60°) = BC / AC Vì tam giác ABC là tam giác vuông cân tại A, nên AC = AB. Do đó: tan(60°) = BC / AB Biết rằng tan(60°) = √3, ta có: √3 = BC / AB Từ đây, ta có: BC = AB √3 Vì tam giác ABC là tam giác vuông cân tại A, nên AB = AC. Do đó: BC = AC √3 Biết rằng AC = h, ta có: BC = h √3 Vì BC = h + 100, ta có: h + 100 = h √3 Rearrange the equation: h √3 - h = 100 Factor out h: h (√3 - 1) = 100 Giải phương trình này: h = 100 / (√3 - 1) Rationalize the denominator: h = 100 (√3 + 1) / ((√3 - 1) (√3 + 1)) h = 100 (√3 + 1) / (3 - 1) h = 100 (√3 + 1) / 2 h = 50 (√3 + 1) h ≈ 50 (1.732 + 1) h ≈ 50 2.732 h ≈ 136.6 Vậy chiều cao của quả đồi là khoảng 137 mét (làm tròn đến chữ số hàng đơn vị). Câu 21. Điều kiện xác định: \( x \neq 0 \) Gọi tọa độ của điểm M là (xM ; yM). Từ giả thiết ta có: xM = 162 - 10 = 152 yM = 43 Thay vào phương trình của parabol ta có: 43 = a × 152^3 suy ra a = 43 : 152^3 = 0,0000108 Phương trình của parabol là: y = 0,0000108 × x^3 Độ cao của cổng Arch là: 0,0000108 × 81^3 = 57,7 (m) Đáp số: 57,7 m Câu 22. Điều kiện xác định: \( x > 0, x \neq 4 \). Ta có: \[ A = \left( \frac{x + 2\sqrt{x}}{x - 2\sqrt{x}} + \frac{\sqrt{x}}{\sqrt{x} - 2} \right) \cdot \frac{1}{\sqrt{x} + 1} \] Chúng ta sẽ đơn giản hóa biểu thức bên trong ngoặc trước: \[ \frac{x + 2\sqrt{x}}{x - 2\sqrt{x}} + \frac{\sqrt{x}}{\sqrt{x} - 2} \] Để cộng hai phân thức này, chúng ta cần quy đồng mẫu số: \[ \frac{x + 2\sqrt{x}}{x - 2\sqrt{x}} + \frac{\sqrt{x}}{\sqrt{x} - 2} = \frac{(x + 2\sqrt{x})(\sqrt{x} - 2) + \sqrt{x}(x - 2\sqrt{x})}{(x - 2\sqrt{x})(\sqrt{x} - 2)} \] Tính tử số: \[ (x + 2\sqrt{x})(\sqrt{x} - 2) + \sqrt{x}(x - 2\sqrt{x}) = x\sqrt{x} - 2x + 2x - 4\sqrt{x} + x\sqrt{x} - 2x = 2x\sqrt{x} - 4\sqrt{x} \] Tính mẫu số: \[ (x - 2\sqrt{x})(\sqrt{x} - 2) = x\sqrt{x} - 2x - 2x + 4\sqrt{x} = x\sqrt{x} - 4x + 4\sqrt{x} \] Do đó: \[ \frac{2x\sqrt{x} - 4\sqrt{x}}{x\sqrt{x} - 4x + 4\sqrt{x}} = \frac{2\sqrt{x}(x - 2)}{\sqrt{x}(x - 4 + 4)} = \frac{2(x - 2)}{x - 4} \] Vậy: \[ A = \frac{2(x - 2)}{x - 4} \cdot \frac{1}{\sqrt{x} + 1} = \frac{2(x - 2)}{(x - 4)(\sqrt{x} + 1)} \] Để \( A \) có giá trị nguyên, \( \frac{2(x - 2)}{(x - 4)(\sqrt{x} + 1)} \) phải là số nguyên. Ta xét các giá trị nguyên của \( x \) sao cho \( x > 0 \) và \( x \neq 4 \): - \( x = 1 \): \( A = \frac{2(1 - 2)}{(1 - 4)(\sqrt{1} + 1)} = \frac{-2}{-3 \cdot 2} = \frac{1}{3} \) (không phải số nguyên) - \( x = 9 \): \( A = \frac{2(9 - 2)}{(9 - 4)(\sqrt{9} + 1)} = \frac{14}{5 \cdot 4} = \frac{7}{10} \) (không phải số nguyên) Vậy không có giá trị nguyên nào của \( x \) thỏa mãn điều kiện trên. Đáp số: Không có giá trị nguyên của \( x \) để \( A \) có giá trị nguyên.