Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
giúp toi câu trả lời chính xác nhất

 0
0
Trả lời câu hỏi của Ẻm Đubai
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.
CÂU TRẢ LỜI



Timi
7 giờ trước
Trợ lý học tập AI - Câu trả lời này chỉ mang tính tham khảo
Để giải quyết bài toán này, chúng ta cần phân tích từng lựa chọn một cách chi tiết.
A. \(\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}\).
Điều này đúng nếu \(G\) là trọng tâm của tam giác \(ABC\). Trọng tâm của tam giác là điểm mà tổng các vectơ từ trọng tâm đến các đỉnh của tam giác bằng vectơ không. Do đó, lựa chọn A là đúng nếu \(G\) là trọng tâm của tam giác \(ABC\).
B. \(\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \overrightarrow{0}\).
Điều này chỉ đúng nếu \(G\) là trọng tâm của tứ diện \(ABCD\), nhưng trong không gian ba chiều, không có khái niệm trọng tâm như trong mặt phẳng. Do đó, lựa chọn B không chính xác trong ngữ cảnh này.
C. \(\overrightarrow{GD} - \overrightarrow{GA} = \overrightarrow{AD}\).
Điều này đúng theo định nghĩa của phép trừ vectơ. Vectơ \(\overrightarrow{GD}\) trừ đi vectơ \(\overrightarrow{GA}\) chính là vectơ \(\overrightarrow{AD}\). Do đó, lựa chọn C là đúng.
D. \(\overrightarrow{DA} + \overrightarrow{DB} + \overrightarrow{DC} = 3\overrightarrow{DG}\).
Điều này đúng nếu \(G\) là trọng tâm của tam giác \(ABC\) và \(D\) là một điểm bất kỳ. Trong trường hợp này, tổng các vectơ từ \(D\) đến các đỉnh của tam giác sẽ bằng ba lần vectơ từ \(D\) đến trọng tâm \(G\). Do đó, lựa chọn D là đúng nếu \(G\) là trọng tâm của tam giác \(ABC\).
Tóm lại, các lựa chọn đúng là A, C và D.
Câu 2:
Để tìm tọa độ của điểm \( M \) trong không gian \( Oxyz \), ta cần hiểu rằng tọa độ của điểm \( M \) chính là các hệ số của các vector đơn vị \(\overrightarrow{i}\), \(\overrightarrow{j}\), và \(\overrightarrow{k}\) trong biểu thức của vector \(\overrightarrow{OM}\).
Cho \(\overrightarrow{OM} = 2\overrightarrow{i} + 3\overrightarrow{j} - 4\overrightarrow{k}\).
Điều này có nghĩa là:
- Hệ số của \(\overrightarrow{i}\) là 2, tương ứng với hoành độ của điểm \( M \).
- Hệ số của \(\overrightarrow{j}\) là 3, tương ứng với tung độ của điểm \( M \).
- Hệ số của \(\overrightarrow{k}\) là -4, tương ứng với cao độ của điểm \( M \).
Vậy tọa độ của điểm \( M \) là \((2; 3; -4)\).
Do đó, đáp án đúng là \( B.~(2; 3; -4) \).
Câu 3:
Để tìm tọa độ của trọng tâm tam giác \( MNP \), ta sử dụng công thức tính tọa độ trọng tâm của tam giác có các đỉnh \( M(x_1, y_1, z_1) \), \( N(x_2, y_2, z_2) \), \( P(x_3, y_3, z_3) \) là:
\[
G\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}, \frac{z_1 + z_2 + z_3}{3}\right)
\]
Áp dụng công thức trên cho tam giác \( MNP \) với các tọa độ đã cho:
- \( M(2, -3, 4) \)
- \( N(1, 2, 3) \)
- \( P(3, -2, 2) \)
Tọa độ của trọng tâm \( G \) là:
\[
G\left(\frac{2 + 1 + 3}{3}, \frac{-3 + 2 - 2}{3}, \frac{4 + 3 + 2}{3}\right)
\]
Tính từng thành phần:
- Hoành độ: \(\frac{2 + 1 + 3}{3} = \frac{6}{3} = 2\)
- Tung độ: \(\frac{-3 + 2 - 2}{3} = \frac{-3}{3} = -1\)
- Cao độ: \(\frac{4 + 3 + 2}{3} = \frac{9}{3} = 3\)
Vậy tọa độ của trọng tâm \( G \) là \( (2, -1, 3) \).
Do đó, đáp án đúng là \( A.~(2, -1, 3) \).
Câu 4:
Để tìm khoảng cách giữa hai điểm \( I(3;5;-7) \) và \( K(-5;5;-1) \) trong không gian Oxyz, ta sử dụng công thức khoảng cách giữa hai điểm trong không gian ba chiều:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\]
Với \( I(3;5;-7) \) và \( K(-5;5;-1) \), ta có:
- \( x_1 = 3 \), \( y_1 = 5 \), \( z_1 = -7 \)
- \( x_2 = -5 \), \( y_2 = 5 \), \( z_2 = -1 \)
Thay các giá trị này vào công thức, ta được:
\[
d = \sqrt{((-5) - 3)^2 + (5 - 5)^2 + ((-1) - (-7))^2}
\]
\[
= \sqrt{(-8)^2 + 0^2 + 6^2}
\]
\[
= \sqrt{64 + 0 + 36}
\]
\[
= \sqrt{100}
\]
\[
= 10
\]
Vậy, khoảng cách giữa hai điểm \( I \) và \( K \) là 10. Do đó, đáp án đúng là C. 10.
Câu 5:
Để tìm tích vô hướng của hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$, ta sử dụng công thức:
\[
\overrightarrow{u} \cdot \overrightarrow{v} = |\overrightarrow{u}| \cdot |\overrightarrow{v}| \cdot \cos(\theta)
\]
Trong đó:
- $|\overrightarrow{u}| = 2$ là độ dài của vectơ $\overrightarrow{u}$.
- $|\overrightarrow{v}| = 3$ là độ dài của vectơ $\overrightarrow{v}$.
- $\theta = 60^\circ$ là góc giữa hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$.
Ta có $\cos(60^\circ) = \frac{1}{2}$.
Thay các giá trị vào công thức, ta được:
\[
\overrightarrow{u} \cdot \overrightarrow{v} = 2 \cdot 3 \cdot \frac{1}{2} = 3
\]
Vậy, $\overrightarrow{u} \cdot \overrightarrow{v} = 3$.
Do đó, đáp án đúng là A. 3.
Câu 1:
Để giải quyết bài toán này, ta cần thực hiện các bước sau:
a) Tọa độ của ra đa
Ra đa được đặt trên đỉnh tháp cao 80 m (tức là 0,08 km) so với mặt đất. Do đó, tọa độ của ra đa là \((0; 0; 0,08)\).
b) Tọa độ của vị trí A
Máy bay cách 300 km về phía đông và 200 km về phía bắc so với tháp, và cách mặt đất 10 km. Do đó, tọa độ của máy bay A là \((300; -200; 10)\).
c) Khoảng cách từ máy bay đến ra đa
Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\]
Thay tọa độ của ra đa \((0; 0; 0,08)\) và máy bay \((300; -200; 10)\) vào công thức:
\[
d = \sqrt{(300 - 0)^2 + (-200 - 0)^2 + (10 - 0,08)^2}
\]
\[
d = \sqrt{300^2 + (-200)^2 + (9,92)^2}
\]
\[
d = \sqrt{90000 + 40000 + 98,4064}
\]
\[
d = \sqrt{130098,4064} \approx 360,69 \text{ km}
\]
d) Khả năng phát hiện của ra đa
Phạm vi theo dõi của ra đa là 500 km. Vì khoảng cách từ máy bay đến ra đa là khoảng 360,69 km, nhỏ hơn 500 km, nên ra đa có thể phát hiện được máy bay tại vị trí A.
Kết luận
a) Tọa độ của ra đa là \((0; 0; 0,08)\).
b) Tọa độ của vị trí A là \((300; -200; 10)\).
c) Khoảng cách từ máy bay đến ra đa là khoảng 360,69 km.
d) Ra đa của trung tâm kiểm soát không lưu có thể phát hiện được máy bay tại vị trí A.
Câu 1:
Để tìm số đo của góc giữa hai vectơ \(\overrightarrow{MN}\) và \(\overrightarrow{AB}\), ta thực hiện các bước sau:
1. Xác định tọa độ các điểm:
Giả sử hình lập phương \(ABCD - A'B'C'D'\) có cạnh bằng \(a\). Ta chọn hệ trục tọa độ sao cho:
- \(A(0, 0, 0)\)
- \(B(a, 0, 0)\)
- \(D(0, a, 0)\)
- \(A'(0, 0, a)\)
- \(D'(0, a, a)\)
- \(C'(a, a, a)\)
2. Tìm tọa độ của điểm \(M\) và \(N\):
- \(M\) là trung điểm của \(A'D'\), nên tọa độ của \(M\) là:
\[
M\left(\frac{0 + 0}{2}, \frac{0 + a}{2}, \frac{a + a}{2}\right) = \left(0, \frac{a}{2}, a\right)
\]
- \(N\) là trung điểm của \(C'D'\), nên tọa độ của \(N\) là:
\[
N\left(\frac{a + 0}{2}, \frac{a + a}{2}, \frac{a + a}{2}\right) = \left(\frac{a}{2}, a, a\right)
\]
3. Tính vectơ \(\overrightarrow{MN}\):
\[
\overrightarrow{MN} = \left(\frac{a}{2} - 0, a - \frac{a}{2}, a - a\right) = \left(\frac{a}{2}, \frac{a}{2}, 0\right)
\]
4. Tính vectơ \(\overrightarrow{AB}\):
\[
\overrightarrow{AB} = (a - 0, 0 - 0, 0 - 0) = (a, 0, 0)
\]
5. Tính góc giữa hai vectơ \(\overrightarrow{MN}\) và \(\overrightarrow{AB}\):
Góc giữa hai vectơ được tính bằng công thức:
\[
\cos \varphi = \frac{\overrightarrow{MN} \cdot \overrightarrow{AB}}{\|\overrightarrow{MN}\| \cdot \|\overrightarrow{AB}\|}
\]
- Tích vô hướng \(\overrightarrow{MN} \cdot \overrightarrow{AB}\):
\[
\overrightarrow{MN} \cdot \overrightarrow{AB} = \frac{a}{2} \cdot a + \frac{a}{2} \cdot 0 + 0 \cdot 0 = \frac{a^2}{2}
\]
- Độ dài của \(\overrightarrow{MN}\):
\[
\|\overrightarrow{MN}\| = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{a}{2}\right)^2 + 0^2} = \sqrt{\frac{a^2}{4} + \frac{a^2}{4}} = \sqrt{\frac{a^2}{2}} = \frac{a\sqrt{2}}{2}
\]
- Độ dài của \(\overrightarrow{AB}\):
\[
\|\overrightarrow{AB}\| = \sqrt{a^2 + 0^2 + 0^2} = a
\]
- Tính \(\cos \varphi\):
\[
\cos \varphi = \frac{\frac{a^2}{2}}{\frac{a\sqrt{2}}{2} \cdot a} = \frac{\frac{a^2}{2}}{\frac{a^2\sqrt{2}}{2}} = \frac{1}{\sqrt{2}}
\]
- Suy ra \(\varphi = 45^\circ\).
Vậy số đo của góc \(\varphi\) là \(45^\circ\).
Câu 2:
Để tìm số đo của góc \(\widehat{ABC}\), ta cần tính góc giữa hai vectơ \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\).
Bước 1: Tính các vectơ \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\).
- Vectơ \(\overrightarrow{BA}\) được tính như sau:
\[
\overrightarrow{BA} = A - B = (1 - 1, 3 - 1, 5 - 3) = (0, 2, 2)
\]
- Vectơ \(\overrightarrow{BC}\) được tính như sau:
\[
\overrightarrow{BC} = C - B = (4 - 1, -2 - 1, 3 - 3) = (3, -3, 0)
\]
Bước 2: Tính tích vô hướng của hai vectơ \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\).
- Tích vô hướng:
\[
\overrightarrow{BA} \cdot \overrightarrow{BC} = (0 \cdot 3) + (2 \cdot -3) + (2 \cdot 0) = 0 - 6 + 0 = -6
\]
Bước 3: Tính độ dài của các vectơ \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\).
- Độ dài của \(\overrightarrow{BA}\):
\[
|\overrightarrow{BA}| = \sqrt{0^2 + 2^2 + 2^2} = \sqrt{0 + 4 + 4} = \sqrt{8} = 2\sqrt{2}
\]
- Độ dài của \(\overrightarrow{BC}\):
\[
|\overrightarrow{BC}| = \sqrt{3^2 + (-3)^2 + 0^2} = \sqrt{9 + 9 + 0} = \sqrt{18} = 3\sqrt{2}
\]
Bước 4: Tính cosin của góc \(\widehat{ABC}\).
- Sử dụng công thức tích vô hướng:
\[
\cos \widehat{ABC} = \frac{\overrightarrow{BA} \cdot \overrightarrow{BC}}{|\overrightarrow{BA}| \cdot |\overrightarrow{BC}|} = \frac{-6}{(2\sqrt{2}) \cdot (3\sqrt{2})} = \frac{-6}{12} = -\frac{1}{2}
\]
Bước 5: Tìm số đo góc \(\widehat{ABC}\).
- Vì \(\cos \widehat{ABC} = -\frac{1}{2}\), nên góc \(\widehat{ABC}\) là \(120^\circ\).
Vậy số đo của góc \(\widehat{ABC}\) là \(120^\circ\).
Hãy giúp mọi người biết câu trả lời này thế nào?
0/5 (0 đánh giá)
 0
0
0 bình luận
Bình luận
Kwaii__
7 giờ trước
câu 1
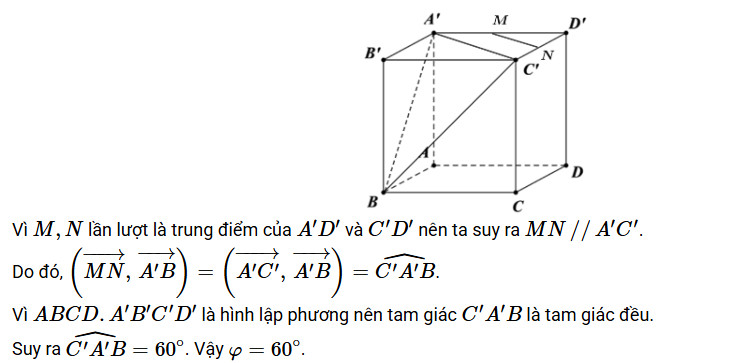
Hãy giúp mọi người biết câu trả lời này thế nào?
0/5 (0 đánh giá)
 0
0
0 bình luận
Bình luận
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
Top thành viên trả lời
Chọn thời gian
Mì 2 Tôm 1.260 Điểm
Huyunh 860 Điểm
Brother 830 Điểm
ᴳᵒᵈ乡xüânĐạt❤ᴾᴿᴼシv 820 Điểm
Nhân Irving 750 Điểm
FQA.vn Nền tảng kết nối cộng đồng hỗ trợ giải bài tập học sinh trong khối K12. Sản phẩm được phát triển bởi CÔNG TY TNHH CÔNG NGHỆ GIA ĐÌNH (FTECH CO., LTD)
Điện thoại: 1900636019
Email: info@fqa.vn
 Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Đống Đa, Thành phố Hà Nội, Việt Nam.
Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Đống Đa, Thành phố Hà Nội, Việt Nam.
Người chịu trách nhiệm quản lý nội dung: Đào Trường Giang
Giấy phép thiết lập MXH số 07/GP-BTTTT do Bộ Thông tin và Truyền thông cấp ngày 05/01/2024
Copyright © 2023 fqa.vn All Rights Reserved



