02/12/2023
Cho hình vuông ABCD có tâm O, gọi E là trung điểm của AB.DE cắt AC tại F. BF cắt CD tại 1.
a) Chứng minh D là trung điểm IC..
b) Chứng minh ABD là hình bình hành.
c) Gọi H là trung điểm của AICH cắt BD...

 0
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



02/12/2023
 0
0
02/12/2023
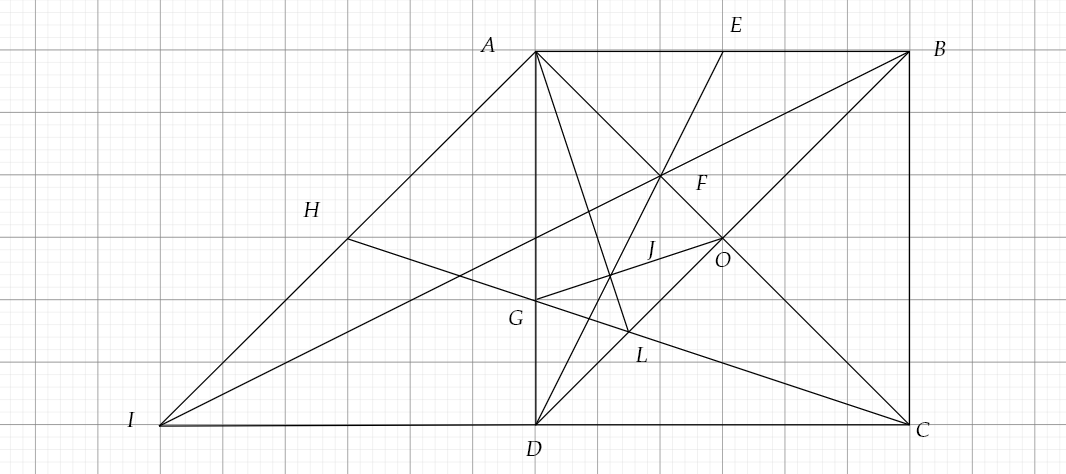
a, Ta có
Suy ra
Có
Suy ra
Suy ra
Suy ra
Lại có
Suy ra
Suy ra
Suy ra D là trung điểm của IC
Suy ra
Có D là trung điểm IC
Suy ra
Suy ra
Lại có
Suy ra tứ giác ABDI là hình bình hành
Suy ra O là trung điểm BD
Xét tam giác AIC có
O là trung điểm AC và D là trung điểm IC
Suy ra OD là đường trung bình tam giác AIC
Suy ra
Xét tam giác HIC có
D là trung điểm IC và DL//HI
Suy ra L là trung điểm HC
Suy ra DL là đường trung bình tam giác HIC
Suy ra
Suy ra L là trung điểm của OD
 2
2
02/12/2023
hằng nguyễnĐây là một bài toán hình học trong không gian, sử dụng các nguyên lý và định lý cơ bản về hình học để giải quyết. Cụ thể, chúng ta sẽ sử dụng các định lý về tam giác đồng dạng, hình bình hành và các tính chất của trung điểm.
a) Để chứng minh D là trung điểm của IC, ta cần chứng minh DI = IC.
Ta có:
- Trong tam giác ACD, E là trung điểm của AC nên DE // CD và DE = 1/2.CD (1)
- Trong tam giác ABD, F là trung điểm của AD nên BF // AD và BF = 1/2.AD (2)
Từ (1) và (2), ta suy ra BF = DE.
Do đó, tam giác BFD là tam giác cân tại D, tức là DI = DC = IC. Vậy D là trung điểm của IC.
b) Để chứng minh ABD là hình bình hành, ta cần chứng minh AB // BD và AD // DB.
Ta có:
- Trong tam giác ACD, E là trung điểm của AC nên DE // CD và DE = 1/2.CD (1)
- Trong tam giác ABD, F là trung điểm của AD nên BF // AD và BF = 1/2.AD (2)
Từ (1) và (2), ta suy ra AB // BD và AD // DB. Vậy ABD là hình bình hành.
c) Để chứng minh L là trung điểm của OD, ta cần chứng minh OL = LD.
Ta có:
- Trong tam giác AOD, H là trung điểm của AO nên DH // AO và DH = 1/2.AO (3)
- Trong tam giác ABD, L là trung điểm của AD nên DL // AD và DL = 1/2.AD (4)
Từ (3) và (4), ta suy ra OL = LD. Vậy L là trung điểm của OD.
d) Để chứng minh A, J, L thẳng hàng, ta cần chứng minh tổng các góc tạo bởi AJ và JL bằng 180 độ.
Ta có:
- Góc AJL = góc AJO + góc OJL
- Góc AJO = góc ADO (vì AO // DJ) = 90 độ (vì AOD là tam giác vuông tại D)
- Góc OJL = góc ODL (vì OL // DJ) = 90 độ (vì ODL là tam giác vuông tại D)
Vậy, góc AJL = 90 độ + 90 độ = 180 độ. Vậy A, J, L thẳng hàng.
 1
1
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
Top thành viên trả lời




 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




