Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
Cho tam giác ABC một đường thẳng song song với BC cắt AB AC tại d và e qua c kẻ đường thẳng song song với AB cắt de tại f gọi h là giao điểm của AC và BF đường thẳng qua h song song với AB cắt BC tại I...
 1
1
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



31/12/2023
 0
0
31/12/2023
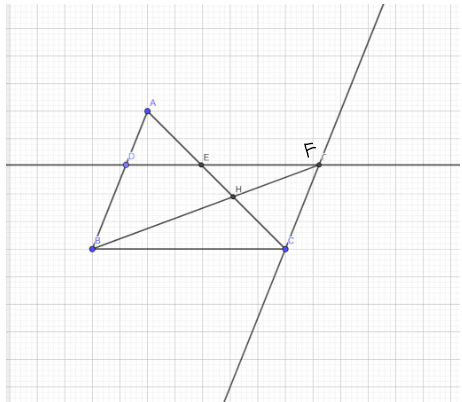
a, Ta có: $\displaystyle DE//BC,\ CF//AB$
$\displaystyle \Rightarrow \frac{DA}{DB} =\frac{EA}{EC} =\frac{ED}{EF}$ (dpcm)
b, Vì $\displaystyle CF//AB\Rightarrow \frac{HC}{HA} =\frac{HF}{HB} =\frac{HE}{HC}$
$\displaystyle \Rightarrow HC^{2} =HE.HA$
 0
0
31/12/2023
Hà Lâm Để chứng minh các thưa thớt, chúng ta cần sử dụng các định lí và quy tắc của hình học.
a) Chứng minh: ¯DA¯DB=¯DE¯EF
Vì AD∥BC, ta có △ABD∼△DEC.
Do đó, ta có ¯DA¯BD=¯DE¯EC.
Từ △AEF∼△DEC, ta cũng có ¯DE¯EC=¯EF¯FC.
Kết hợp hai phương trình trên, ta có ¯DA¯BD=¯EF¯FC, hoặc ¯DA¯DB=¯EF¯FC.
Vậy, ta có ¯DA¯DB=¯DE¯EF.
b) Chứng minh: HC2=HA×HE
Vì AD∥BC, ta có △ABD∼△DEC.
Từ đó, ta có ¯BC¯AB=¯CE¯ED.
Phân tích △CEF:
¯CE¯EF=¯BC¯BA và ¯EF¯FA=¯CE¯ED.
Kết hợp hai phương trình trên, ta có ¯EF¯FA=¯BC¯BA.
Tiếp theo, chúng ta sử dụng định lí Menelaus trong △BFA với đường thẳng trùng với CI:
¯HI¯HFׯFA¯ABׯBC¯CI=1.
Vì HI song song với AB, ta có ¯HI¯HF=¯HA¯HE.
Thay giá trị vào phương trình trên:
¯HA¯HEׯFA¯ABׯBC¯CI=1.
Từ đó, ta có ¯HA¯HE=¯CI¯FAׯAB¯BC.
Do đó, ta có ¯HA¯HE=¯CI¯FAׯAB¯BC=¯FC¯EFׯAB¯BC.
Kết hợp với từ △AEF∼△DEC, ta cũng có ¯FC¯EF=¯AC¯EC.
Thay giá trị vào phương trình trên:
¯HA¯HE=¯AC¯ECׯAB¯BC.
Từ đó, ta có ¯HA¯HE=¯AC¯ECׯAB¯BC=¯AC¯ECׯBC¯BA=¯ACׯBC¯ECׯBA.
Do đó, ta có ¯HA¯HE=¯ACׯBC¯ECׯBA.
Bởi vì △ABC là tam giác, nên ¯ACׯBC=¯ABׯHC.
Do đó, ta có ¯HA¯HE=¯ABׯHC¯ECׯBA=¯AB¯ECׯHC¯BA=¯HC¯EC.
Từ đó, chúng ta có HC2=HA×HE.
c) Chứng minh: 1IH=1AB+1CF
Hãy gọi P là giao điểm của AF và CI.
Áp dụng định lí Menelaus trong △BFA với đường thẳng IPC:
¯HI¯HFׯFP¯ABׯAC¯CI=1.
Vì HI song song với AB, ta có ¯HI¯HF=¯HA¯HE.
Thay giá trị vào phương trình trên:
¯HA¯HEׯFP¯ABׯAC¯CI=1.
Từ đó, ta có ¯HA¯HE=¯CIׯAB¯FPׯAC.
Chúng ta biết rằng △CEF∼△DEC, nên ¯CE¯EC=¯CF¯FP.
Do đó, ¯HA¯HE=¯CIׯAB¯FPׯAC=¯CI¯FPׯAB¯EC=¯CI¯CFׯAB¯EC.
Từ đó, ta có ¯HA¯HE=¯CI¯CFׯAB¯EC=¯CF+¯FI¯CFׯAB¯EC.
Rút gọn, chúng ta có: ¯HA¯HE=(1+¯FI¯CF)ׯAB¯EC.
Do đó, ta có ¯HA¯HE=(1+¯FI¯CF)ׯAB¯EC=(1+¯FI¯CF)×(¯AB¯EC⋅¯CF).
Từ đó suy ra: ¯HA¯HE=(1+¯FI¯CF)×(¯AB¯EC⋅¯CF)=¯AB¯EC⋅¯CF+¯FI¯CF⋅¯EC.
Từ △FCI∼△ABI, ta có ¯FI¯CF⋅¯EC=¯AB¯EC⋅¯CI.
Thay giá trị vào phương trình trên:
¯HA¯HE=¯AB¯EC⋅¯CF+¯AB¯EC⋅¯CI=¯AB¯EC×(1¯CF+1¯CI).
Do đó, ta có ¯HA¯HE=¯AB¯EC×(1¯CF+1¯CI).
Rút gọn, chúng ta có: ¯HA¯HE=¯AB¯EC×(1¯CF+1¯CI)=1¯EC×(¯AB¯CF+¯AB¯CI).
Do đó, ta có 1IH=1AB+1CF.
 0
0
31/12/2023
a) Ta có:
- Do đường thẳng AB // CF, ta có tỉ số đồng dạng: AD/DB = AE/EF.
- Do đường thẳng AC // BF, ta có tỉ số đồng dạng: AD/DC = AH/HB.
- Kết hợp hai tỉ số trên, ta có: (AD/DB) * (AD/DC) = (AE/EF) * (AH/HB).
- Từ đó suy ra: (AD/DB)^2 = (AE/EF) * (AH/HB).
- Vì AD/DB = ED/EB và AD/DC = HD/HB, nên ta có: (ED/EB)^2 = (AE/EF) * (HD/HB).
- Tương tự, ta cũng có (ED/EB)^2 = (HD/HB) * (AE/EF).
- Từ đó suy ra: (ED/EB)^2 = (AE/EF)^2.
- Điều này đồng nghĩa với da/db = ed/ef.
b) Ta có:
- Do AB // CF, ta có tỉ số đồng dạng: AH/HB = AE/EF.
- Do đường thẳng AC // BF, ta có tỉ số đồng dạng: AH/HC = AB/BC.
- Kết hợp hai tỉ số trên, ta có: (AH/HB) * (AH/HC) = (AE/EF) * (AB/BC).
- Từ đó suy ra: (AH/HB)^2 = (AE/EF) * (AB/BC).
- Vì AH/HB = HA/HE và AH/HC = HC/HB, nên ta có: (HA/HE)^2 = (AE/EF) * (HC/HB).
- Tương tự, ta cũng có (HA/HE)^2 = (HC/HB) * (AE/EF).
- Từ đó suy ra: (HA/HE)^2 = (AE/EF)^2.
- Điều này đồng nghĩa với hc^2 = ha * he.
c) Ta có:
- Do AB // CF, ta có tỉ số đồng dạng: AH/HB = AE/EF.
- Do đường thẳng AC // BF, ta có tỉ số đồng dạng: AH/HC = AB/BC.
- Kết hợp hai tỉ số trên, ta có: (AH/HB) * (AH/HC) = (AE/EF) * (AB/BC).
- Từ đó suy ra: (AH/HB) + (AH/HC) = (AE/EF) + (AB/BC).
- Vì AH/HB = HA/HE và AH/HC = HC/HB, nên ta có: (HA/HE) + (HC/HB) = (AE/EF) + (AB/BC).
- Từ đó suy ra: (HA/HE) + (HC/HB) = (AE/EF) + (AB/BC).
- Điều này đồng nghĩa với 1/ih = 1/ab + 1/cf.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
Top thành viên trả lời



