Đăng ký học gia sư
Tất cả
Hỏi bài tập 
Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống 
Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
18/08/2024
Cho tứ giác lồi ABCD có góc A = góc B và BC = AD. Chứng minh:
a) tam giác DAB = tam giác CBA rồi suy ra BD = AC
b) tam giác ACD = tam giác BDC rồi suy ra góc ADC = góc BCD
c) ABCD là hình thang cân
Các...
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.
18/08/2024
1 
18/08/2024
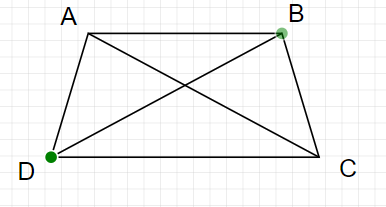
a) Xét $\triangle D A B$ và $\triangle C B A$ có:
AB chung
$góc B A D=góc A B C($ giả thiết)
$A D=B C$ (giả thiết)
$
\begin{aligned}
& \Rightarrow \triangle D A B=\Delta C B A(c-g-c) \\
& \Rightarrow B D=A C
\end{aligned}
$
b)Xét $\triangle A D C$ và $\triangle B C D$ có
$
\begin{aligned}
& A D=B C \\
& A C=B D
\end{aligned}
$
DC chung
$
\Rightarrow \triangle A D C=\Delta B C D(c-c-c)
$
Do $\triangle A D C=\triangle B C D$
$
\Rightarrow \mathrm{góc ADC}=\mathrm{gócBCD}
$
c) Tứ giác $\displaystyle ABCD$ có $\displaystyle AC,BD$ là 2 đường chéo mà $\displaystyle AC=BD$(cmt)
$\displaystyle \Rightarrow ABCD$ là hình thang cân (tính chất)
0 
18/08/2024
Chắc chắn rồi! Chúng ta sẽ chứng minh từng phần theo yêu cầu.
### Đề bài
Cho tứ giác lồi \(ABCD\) với \( \angle A = \angle B\) và \( BC = AD\). Chứng minh:
a) Tam giác \(DAB = \) tam giác \(CBA\) rồi suy ra \(BD = AC\).
b) Tam giác \(ACD = \) tam giác \(BDC\) rồi suy ra \( \angle ADC = \angle BCD\).
c) Tứ giác \(ABCD\) là hình thang cân.
### Chứng minh
**a) Chứng minh tam giác \(DAB\) bằng tam giác \(CBA\)**
Chúng ta sẽ sử dụng điều kiện hai tam giác bằng nhau:
- \( \angle A = \angle B \) (theo giả thiết)
- \( BC = AD \) (theo giả thiết)
- \( \angle DAB = \angle CBA \) (theo giả thiết)
Để chứng minh hai tam giác này bằng nhau, chúng ta cần chứng minh thêm một cạnh nữa. Chúng ta sẽ sử dụng cạnh chung \(AB\).
Vì vậy:
- Tam giác \(DAB\) có các góc \( \angle DAB\) và \( \angle CBA\) bằng nhau.
- Cạnh \(AD = BC\).
- Cạnh \(AB\) chung.
Do đó, tam giác \(DAB\) bằng tam giác \(CBA\) theo tiêu chuẩn góc-góc-cạnh (G-G-C).
Suy ra:
\[ BD = AC \]
**b) Chứng minh tam giác \(ACD = \) tam giác \(BDC\)**
Chúng ta đã có:
- \( BD = AC \) (theo kết quả phần a)
- \( \angle CAD = \angle CBD \) (do \(\angle A = \angle B\))
- \( \angle ACD = \angle BDC \) (do góc bù của nhau)
Do đó, hai tam giác \(ACD\) và \(BDC\) cũng bằng nhau theo tiêu chuẩn góc-cạnh-góc (G-C-G).
Suy ra:
\[ \angle ADC = \angle BCD \]
**c) Chứng minh tứ giác \(ABCD\) là hình thang cân**
Tứ giác \(ABCD\) là hình thang nếu có một cặp cạnh đối song song. Để chứng minh điều này, chúng ta phải chứng minh rằng \(AB\) song song với \(CD\) và \(AD\) song song với \(BC\).
Từ các kết quả trên:
- Tam giác \(DAB\) bằng tam giác \(CBA\), nên các góc tương ứng bằng nhau:
- \( \angle DAB = \angle CBA \)
- \( \angle ADB = \angle CBA \)
- \( \angle ABD = \angle BCA \)
- Tam giác \(ACD\) bằng tam giác \(BDC\):
- \( \angle ACD = \angle BDC \)
- \( \angle CAD = \angle CBD \)
- \( \angle ADC = \angle BCD \)
Từ đây, chúng ta có thể thấy rằng các góc đối diện trong tứ giác \(ABCD\) bằng nhau và do đó tứ giác này có hai cặp góc đối diện bằng nhau. Điều này chứng minh rằng tứ giác \(ABCD\) là hình thang cân.
### Tóm lại
- Tam giác \(DAB = CBA\) và \(BD = AC\).
- Tam giác \(ACD = BDC\) và \( \angle ADC = \angle BCD\).
- Tứ giác \(ABCD\) là hình thang cân.
0 Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
Top thành viên trả lời
Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Ô Chợ Dừa, Quận Đống Đa, Thành phố Hà Nội, Việt Nam.