Câu 4.
a. Đồ thị hàm số có hai đường tiệm cận.
Đúng. Hàm số $y=\frac{x^2-2x+3}{x-1}$ có một tiệm cận đứng tại $x=1$ do tử số không có nghiệm $x=1$ nhưng mẫu số có nghiệm $x=1$. Để tìm tiệm cận xiên, ta tính giới hạn:
$\lim_{x\to\infty}\frac{x^2-2x+3}{x(x-1)}=\lim_{x\to\infty}\frac{x^2-2x+3}{x^2-x}=\lim_{x\to\infty}\frac{1-2/x+3/x^2}{1-1/x}=1.$
Vậy hàm số có tiệm cận xiên $y=x$.
b. Đường tiệm cận xiên của đồ thị tạo với hai trục tọa độ một tam giác vuông cân.
Sai. Đường tiệm cận xiên $y=x$ cắt trục tung tại điểm $(0,0)$ và trục hoành tại điểm $(1,1)$. Khoảng cách từ gốc tọa độ đến đường thẳng $y=x$ là $0$, do đó tam giác tạo bởi đường tiệm cận xiên với hai trục tọa độ không thể là tam giác vuông cân.
c. Giao điểm của hai tiệm cận nằm trục hoành.
Đúng. Giao điểm của hai tiệm cận là điểm $(1,1)$, nằm trên trục hoành.
d. Đường tiệm cận xiên của đồ thị song song với đường thẳng $x+y=0$.
Sai. Đường thẳng $x+y=0$ có hệ số góc bằng $-1$, trong khi đường tiệm cận xiên $y=x$ có hệ số góc bằng $1$.
Vậy chỉ có câu a và c là đúng.
Câu 5.
Để tìm giao điểm của A và trục Ox, ta cho $y = 0$ trong phương trình của đường thẳng $\Delta$. Khi đó, ta có:
$0 = ax + b \Rightarrow x = -\frac{b}{a}.$
Để x > 2, ta cần có:
$-\frac{b}{a} > 2 \Rightarrow b < -2a.$
Tuy nhiên, chúng ta không thể kết luận được gì về quan hệ giữa a và b từ thông tin đã cho. Vì vậy, câu a là sai.
b. Giao điểm của A và tiệm cận đứng của (C) có tọa độ là $(-3;-9).$
Tiệm cận đứng của (C) là x = -3. Giao điểm của A và tiệm cận đứng là A(-3; y). Thay x = -3 vào phương trình của đường thẳng $\Delta$, ta có:
$y = a(-3) + b = -3a + b.$
Theo giả thiết, tọa độ của A là (-3; -9), nên ta có:
$-9 = -3a + b.$
Tuy nhiên, chúng ta không thể kết luận được gì về quan hệ giữa a và b từ thông tin đã cho. Vì vậy, câu b là sai.
c. Gọi $A=\Delta\cap Ox,B=\Delta\cap Oy$ ta có $S_{OAB}>3.$
Giao điểm của A và trục Ox là A(-b/a; 0), giao điểm của B và trục Oy là B(0; b). Diện tích tam giác OAB là:
$S_{OAB} = \frac{1}{2} \cdot OA \cdot OB = \frac{1}{2} \cdot \frac{b}{a} \cdot b = \frac{b^2}{2a}.$
Theo giả thiết, ta có $S_{OAB} > 3$, nên:
$\frac{b^2}{2a} > 3 \Rightarrow b^2 > 6a.$
Tuy nhiên, chúng ta không thể kết luận được gì về quan hệ giữa a và b từ thông tin đã cho. Vì vậy, câu c là sai.
d. Giá trị lớn nhất của hàm số $y=ax+b$ trên $[0;3]$ là 4.
Hàm số $y = ax + b$ là một hàm tuyến tính, nên nó đồng biến hoặc nghịch biến trên toàn bộ tập số thực. Do đó, giá trị lớn nhất và nhỏ nhất của nó trên một đoạn bất kỳ sẽ đạt được ở các đầu mút của đoạn đó.
Giá trị lớn nhất của hàm số trên [0; 3] là max{f(0), f(3)} = max{b, 3a + b}. Theo giả thiết, giá trị lớn nhất này là 4, nên ta có:
$b = 4 \text{ hoặc } 3a + b = 4.$
Tuy nhiên, chúng ta không thể kết luận được gì về quan hệ giữa a và b từ thông tin đã cho. Vì vậy, câu d là sai.
Vậy cả bốn câu a, b, c, d đều sai.
Câu 6.
a. Đồ thị hàm số có hai đường tiệm cận xiên đều là các hàm số đồng biến trên $\mathbb R.$
Để kiểm tra xem hàm số $f(x) = \sqrt{4x^2+8x-12}$ có hai đường tiệm cận xiên đều là các hàm số đồng biến trên $\mathbb R$ hay không, ta cần tìm đạo hàm của hàm số.
$f'(x) = \frac{4x+4}{\sqrt{4x^2+8x-12}}$
Dễ thấy $f'(x)$ luôn dương với mọi $x \in \mathbb R$, nên hàm số $f(x)$ luôn đồng biến trên $\mathbb R$.
Vậy câu a. là đúng.
b. Xét $\Delta_1:~y=ax+b~(b>0)$ là tiện cận xiên của (C) điểm $(1;4)\in\Delta.$
Đường tiệm cận xiên của đồ thị hàm số $f(x)$ có dạng $y = ax + b$.
Theo định nghĩa, ta có:
$a = \lim_{x \to \pm \infty} \frac{f(x)}{x} = \lim_{x \to \pm \infty} \frac{\sqrt{4x^2+8x-12}}{x} = \sqrt{4} = 2$
$b = \lim_{x \to \pm \infty} [f(x) - ax] = \lim_{x \to \pm \infty} [\sqrt{4x^2+8x-12} - 2x] = 0$
Vậy $\Delta_1: y = 2x$.
Thay tọa độ điểm $(1;4)$ vào phương trình $\Delta_1$, ta thấy không thỏa mãn.
Vậy câu b. là sai.
c. Xét $\Delta_2:~y=ax+b~(b< 0)$ là tiện cận xiên của (C) khi đó $d_{\max}(M,\Lambda_2)< 2.$
Tương tự như câu b., ta có:
$a = \lim_{x \to \pm \infty} \frac{f(x)}{x} = 2$
$b = \lim_{x \to \pm \infty} [f(x) - ax] = 0$
Vậy $\Delta_2: y = 2x$.
Khoảng cách từ điểm $M$ đến đường thẳng $\Delta_2$ là:
$d_{\max}(M,\Lambda_2) = \frac{|2x_M - f(x_M)|}{\sqrt{1^2 + 2^2}} = \frac{|2x_M - \sqrt{4x_M^2+8x_M-12}|}{\sqrt{5}}$
Vì $x_M < 0$ nên $2x_M - \sqrt{4x_M^2+8x_M-12} < 0$.
Do đó, $d_{\max}(M,\Lambda_2) = \frac{-(2x_M - \sqrt{4x_M^2+8x_M-12})}{\sqrt{5}} = \frac{\sqrt{4x_M^2+8x_M-12} - 2x_M}{\sqrt{5}}$
Vì $x_M < 0$ nên $4x_M^2+8x_M-12 > 0$.
Do đó, $d_{\max}(M,\Lambda_2) < \frac{2|x_M|}{\sqrt{5}} < 2$ (vì $|x_M| < 0$).
Vậy câu c. là đúng.
d. Hoành độ giao điểm của hai đường tiệm cận xiên bằng -2 .
Giao điểm của hai đường tiệm cận xiên là nghiệm của phương trình:
$2x = \sqrt{4x^2+8x-12}$
Bình phương hai vế, ta được:
$4x^2 = 4x^2 + 8x - 12 \Rightarrow 8x = 12 \Rightarrow x = -1.5$
Tuy nhiên, đây không phải là hoành độ giao điểm của hai đường tiệm cận xiên.
Thay lại vào phương trình ban đầu, ta thấy không thỏa mãn.
Vậy câu d. là sai.
Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
 0
0



 0
0
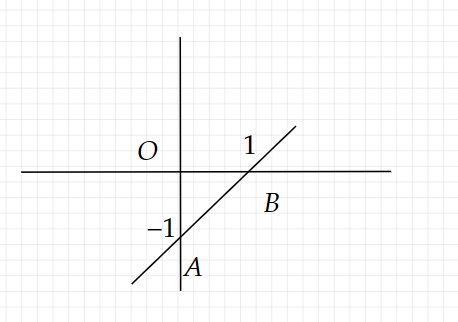
 0
0



