30/09/2024
cho tâm giác MNP cân tại M có MA là trung tuyến F và E lần lượt là trung điểm MP và MN , k là điểm đối xứng của A qua E
a) chứng minh MEAF là hình thoi
b) chứng minh AK=MP
c) tam giác MNP là hình gì đ...
Làm sao để có câu trả lời hay nhất?
- Luôn có GIẢI THÍCH các bước giải
- Không copy câu trả lời của Timi
- Không sao chép trên mạng
- Không spam câu trả lời để nhận điểm
- Spam sẽ bị khóa tài khoản



30/09/2024
 0
0
30/09/2024
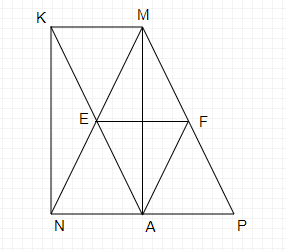
a.
Trong MNP có:
E,F là trung điểm của MN, MP
Suy ra EF là đường trung bình trong tam giác MNP
Tam giác MNP cân tại M có MA là đường trung tuyến
Suy ra MA đồng thời là đường cao
Tam giác MNP có:
AE là đường trung bình
F là trung điểm MP
Tứ giác MEAF có:
Suy ra MEAF là hình thoi
b.
Ta có:
E là trung điểm của MN
E là trung điểm của AK
Tứ giác AMKN có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Suy ra AMKN là hình bình hành
Lại có: MA là đường trung tuyến trong tam giác MNP cân tại M
Suy ra MH đồng thời là đường cao
Suy ra AMKN là hình chữ nhật
Mà MN=MP (MNP cân tại M)
c.
MANK là hình chữ nhật
Để MANK là hình vuông thì AM=AN
Mà MA là đường trung tuyến, AN là nửa cạnh huyền
Vậy để MANK là hình vuông thì MNP là tam giác vuông cân tại M
 0
0
30/09/2024
phương Thảo Giải:
a) Chứng minh MEAF là hình thoi
Tứ giác MEAF có:
ME // AF (do E là trung điểm của MN, F là trung điểm của MP)
MF // AE (tương tự)
MA = AF (do K là điểm đối xứng của A qua E, nên AE = EK = MA)
ME = AF (do ME // AF và MA = AF)
Vậy MEAF là hình bình hành có hai cạnh kề bằng nhau (MA = AF), nên MEAF là hình thoi.
b) Chứng minh AK = MP
Ta có:
AK = 2AE (do K là điểm đối xứng của A qua E)
MP = 2MF (do F là trung điểm của MP)
AE = MF (do MEAF là hình thoi)
Từ đó suy ra AK = MP.
c) Tam giác MNP là hình gì để MANK là hình vuông
Để tứ giác MANK là hình vuông thì:
MANK phải là hình thoi (đã chứng minh ở câu a)
Một góc của MANK phải bằng 90 độ.
Để góc MAN = 90 độ thì tam giác AMN vuông cân tại A.
Mà AM là đường trung tuyến của tam giác cân MNP, nên AM cũng là đường cao.
Vậy để MANK là hình vuông thì tam giác MNP vuông cân tại M.
Kết luận:
MEAF là hình thoi.
AK = MP.
Để MANK là hình vuông thì tam giác MNP phải vuông cân tại M.
Lưu ý:
Để hiểu rõ hơn về bài toán, bạn có thể vẽ hình và theo dõi từng bước chứng minh. Ngoài ra, bạn có thể tham khảo thêm các tính chất của hình thoi, hình vuông và các định lý liên quan trong hình học.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
1 giờ trước
Top thành viên trả lời




 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




