help meeeeeee

Câu 6. Để đồ thị hàm số $y = x^3 - 3mx^2 + 2m$ cắt trục hoành tại ba điểm phân biệt có hoành độ lập thành cấp số cộng, ta cần tìm các giá trị của tham số thực $m$ sao cho phương trình $x^3 - 3mx^2 + 2m = 0$ có ba nghiệm phân biệt lập thành cấp số cộng. Gọi ba nghiệm của phương trình là $a-d$, $a$, và $a+d$. Theo định lý Viète, ta có: \[ (a-d) + a + (a+d) = 3a = 3m \implies a = m \] \[ (a-d)a + a(a+d) + (a-d)(a+d) = -3m^2 + 2m = 0 \] \[ (a-d)a(a+d) = -2m = 0 \] Từ $(a-d)a(a+d) = -2m$, ta có: \[ (m-d)m(m+d) = -2m \] \[ m(m^2 - d^2) = -2m \] \[ m^3 - md^2 = -2m \] \[ m^3 + 2m = md^2 \] \[ m(m^2 + 2) = md^2 \] \[ m^2 + 2 = d^2 \] Do đó, $d^2 = m^2 + 2$. Để phương trình có ba nghiệm phân biệt, $d^2 > 0$, suy ra $m^2 + 2 > 0$, điều này luôn đúng với mọi $m$. Do đó, $m$ có thể nhận mọi giá trị thực. Vậy có vô số giá trị của tham số thực $m$ để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt có hoành độ lập thành cấp số cộng. Đáp số: Vô số giá trị của $m$. Câu 7. Để tìm giao điểm của đường thẳng $\Delta$ với đồ thị của hàm số, ta thay phương trình của đường thẳng vào phương trình của hàm số: \[ y = 2x + 1 \] \[ y = x^3 - x + 3 \] Ta có phương trình: \[ 2x + 1 = x^3 - x + 3 \] Rearrange the equation: \[ x^3 - 3x + 2 = 0 \] Phương trình này có thể được phân tích thành: \[ (x - 1)(x^2 + x - 2) = 0 \] Phân tích tiếp: \[ (x - 1)(x - 1)(x + 2) = 0 \] Từ đây, ta tìm được các nghiệm: \[ x = 1 \quad \text{với bội số 2} \] \[ x = -2 \] Do đó, ta có hai giao điểm: 1. \( x = 1 \) 2. \( x = -2 \) Vì \( x_B < x_A \), ta có: \[ x_B = -2 \] Thay \( x_B = -2 \) vào phương trình của đường thẳng để tìm \( y_B \): \[ y_B = 2(-2) + 1 = -4 + 1 = -3 \] Vậy tọa độ của điểm B là \( (-2, -3) \). Cuối cùng, ta tính \( x_B + y_B \): \[ x_B + y_B = -2 + (-3) = -5 \] Đáp số: \( x_B + y_B = -5 \) Câu 8. Để tìm giá trị của \( m \) sao cho đường thẳng \( d \) cắt đồ thị \( (C_m) \) tại 3 điểm phân biệt, ta cần giải phương trình hoành độ giao điểm của chúng. Phương trình hoành độ giao điểm: \[ x^3 + 3mx^2 - m^3 = m^2x + 2m^3 \] \[ x^3 + 3mx^2 - m^2x - 3m^3 = 0 \] Gọi ba nghiệm của phương trình này là \( x_1, x_2, x_3 \). Ta có: \[ x^3 + 3mx^2 - m^2x - 3m^3 = (x - x_1)(x - x_2)(x - x_3) \] Theo định lý Viète, ta có: \[ x_1 + x_2 + x_3 = -3m \] \[ x_1x_2 + x_2x_3 + x_3x_1 = -m^2 \] \[ x_1x_2x_3 = 3m^3 \] Ta cần tính \( x_1^4 + x_2^4 + x_3^4 \): \[ x_1^4 + x_2^4 + x_3^4 = (x_1^2)^2 + (x_2^2)^2 + (x_3^2)^2 \] Áp dụng công thức bình phương: \[ x_1^2 + x_2^2 + x_3^2 = (x_1 + x_2 + x_3)^2 - 2(x_1x_2 + x_2x_3 + x_3x_1) \] \[ x_1^2 + x_2^2 + x_3^2 = (-3m)^2 - 2(-m^2) \] \[ x_1^2 + x_2^2 + x_3^2 = 9m^2 + 2m^2 \] \[ x_1^2 + x_2^2 + x_3^2 = 11m^2 \] Bây giờ, ta tính \( x_1^4 + x_2^4 + x_3^4 \): \[ x_1^4 + x_2^4 + x_3^4 = (x_1^2)^2 + (x_2^2)^2 + (x_3^2)^2 \] \[ x_1^4 + x_2^4 + x_3^4 = (x_1^2 + x_2^2 + x_3^2)^2 - 2(x_1^2x_2^2 + x_2^2x_3^2 + x_3^2x_1^2) \] Ta biết: \[ x_1^2x_2^2 + x_2^2x_3^2 + x_3^2x_1^2 = (x_1x_2 + x_2x_3 + x_3x_1)^2 - 2x_1x_2x_3(x_1 + x_2 + x_3) \] \[ x_1^2x_2^2 + x_2^2x_3^2 + x_3^2x_1^2 = (-m^2)^2 - 2(3m^3)(-3m) \] \[ x_1^2x_2^2 + x_2^2x_3^2 + x_3^2x_1^2 = m^4 + 18m^4 \] \[ x_1^2x_2^2 + x_2^2x_3^2 + x_3^2x_1^2 = 19m^4 \] Do đó: \[ x_1^4 + x_2^4 + x_3^4 = (11m^2)^2 - 2(19m^4) \] \[ x_1^4 + x_2^4 + x_3^4 = 121m^4 - 38m^4 \] \[ x_1^4 + x_2^4 + x_3^4 = 83m^4 \] Theo đề bài, ta có: \[ 83m^4 = 83 \] \[ m^4 = 1 \] \[ m = \pm 1 \] Vậy \( m_1 = 1 \) và \( m_2 = -1 \). Do đó: \[ m_1 + m_2 = 1 + (-1) = 0 \] Đáp số: \( m_1 + m_2 = 0 \) Câu 9. Để tìm giao điểm của đường thẳng $\Delta$ với đồ thị của hàm số, ta thay phương trình của đường thẳng vào phương trình của hàm số: \[ y = 2x + 1 \] \[ y = x^3 - x + 3 \] Ta có phương trình: \[ 2x + 1 = x^3 - x + 3 \] Rearrange the equation: \[ x^3 - 3x + 2 = 0 \] Phương trình này có thể được phân tích thành: \[ (x - 1)(x^2 + x - 2) = 0 \] Phân tích tiếp: \[ (x - 1)(x - 1)(x + 2) = 0 \] Vậy phương trình có các nghiệm: \[ x = 1 \quad \text{và} \quad x = -2 \] Do đó, tọa độ của các giao điểm là: - Khi \( x = 1 \): \[ y = 2(1) + 1 = 3 \] Vậy giao điểm là \( A(1, 3) \). - Khi \( x = -2 \): \[ y = 2(-2) + 1 = -3 \] Vậy giao điểm là \( B(-2, -3) \). Theo đề bài, \( x_B < x_A \), nên \( B(-2, -3) \) và \( A(1, 3) \). Vậy \( x_B + y_B = -2 + (-3) = -5 \). Đáp số: \( x_B + y_B = -5 \). 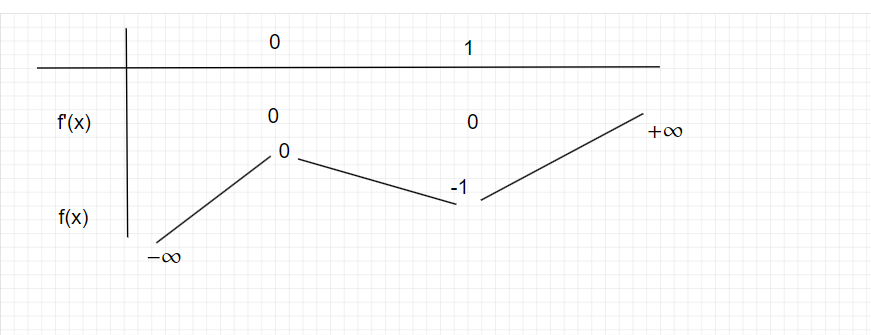Câu 10. Để phương trình $2x^3 - 3x^2 = 2m + 1$ có đúng hai nghiệm phân biệt, ta cần tìm các giá trị của $m$ sao cho đồ thị hàm số $y = 2x^3 - 3x^2$ cắt đường thẳng $y = 2m + 1$ tại đúng hai điểm. Bước 1: Xét hàm số $f(x) = 2x^3 - 3x^2$. - Tính đạo hàm: $f'(x) = 6x^2 - 6x = 6x(x - 1)$. - Tìm các điểm cực trị: - $f'(x) = 0 \Rightarrow 6x(x - 1) = 0 \Rightarrow x = 0$ hoặc $x = 1$. - $f(0) = 0$, $f(1) = -1$. Bước 2: Xác định các giá trị của $m$ để phương trình có đúng hai nghiệm phân biệt. - Đồ thị của $y = 2x^3 - 3x^2$ có cực đại tại $(0, 0)$ và cực tiểu tại $(1, -1)$. - Để phương trình có đúng hai nghiệm phân biệt, đường thẳng $y = 2m + 1$ phải đi qua cực đại hoặc cực tiểu của đồ thị hàm số $y = 2x^3 - 3x^2$. Bước 3: Xác định các giá trị của $m$. - Nếu đường thẳng đi qua cực đại $(0, 0)$: $2m + 1 = 0 \Rightarrow m = -\frac{1}{2}$. - Nếu đường thẳng đi qua cực tiểu $(1, -1)$: $2m + 1 = -1 \Rightarrow m = -1$. Tập S bao gồm các giá trị $m = -\frac{1}{2}$ và $m = -1$. Tổng các phần tử của S là: \[ -\frac{1}{2} + (-1) = -\frac{3}{2} \] Đáp số: $-\frac{3}{2}$. Câu 1. Để giải quyết câu hỏi này, chúng ta sẽ dựa vào bảng biến thiên của hàm số \( f(x) = \frac{ax + 1}{bx + c} \) và các tính chất của hàm phân thức. 1. Xác định các giới hạn và điểm bất định: - Từ bảng biến thiên, ta thấy rằng hàm số \( f(x) \) có hai đường tiệm cận đứng tại \( x = -1 \) và \( x = 2 \). Điều này cho thấy \( bx + c = 0 \) tại \( x = -1 \) và \( x = 2 \). - Do đó, ta có \( b(-1) + c = 0 \Rightarrow -b + c = 0 \Rightarrow c = b \). - Tương tự, \( b(2) + c = 0 \Rightarrow 2b + c = 0 \Rightarrow c = -2b \). 2. Giải hệ phương trình: - Kết hợp hai phương trình \( c = b \) và \( c = -2b \), ta có: \[ b = -2b \Rightarrow 3b = 0 \Rightarrow b = 0 \] - Điều này mâu thuẫn với việc \( b \neq 0 \) vì nếu \( b = 0 \), hàm số không còn là phân thức. Do đó, ta phải xem xét lại các điều kiện khác. 3. Xét dấu của các hệ số: - Từ bảng biến thiên, ta thấy rằng hàm số \( f(x) \) tăng từ \( -\infty \) đến \( -1 \), giảm từ \( -1 \) đến \( 2 \), và tiếp tục tăng từ \( 2 \) đến \( +\infty \). Điều này cho thấy \( a \) và \( b \) phải có cùng dấu để đảm bảo các đoạn tăng/giảm đúng theo bảng biến thiên. - Ta cũng thấy rằng \( f(x) \) có giá trị âm khi \( x < -1 \) và \( x > 2 \), và giá trị dương khi \( -1 < x < 2 \). Điều này cho thấy \( c \) phải có dấu trái ngược với \( a \) và \( b \). 4. Tổng kết các điều kiện: - \( a \) và \( b \) có cùng dấu. - \( c \) có dấu trái ngược với \( a \) và \( b \). Do đó, trong các số \( a, b, \) và \( c \), chỉ có một số dương. Đáp án: Trong các số \( a, b, \) và \( c \), có 1 số dương. Câu 2. Để giải quyết bài toán này, chúng ta cần tìm giá trị của \(a\), \(b\), và \(c\) từ đồ thị hàm số đã cho. Sau đó, chúng ta sẽ tính giá trị của biểu thức \(T = a + 2b + 3c\). Bước 1: Xác định các giá trị \(a\), \(b\), và \(c\) từ đồ thị. - Từ đồ thị, ta thấy rằng điểm \((0, 1)\) nằm trên đồ thị hàm số. Điều này cho thấy \(f(0) = 1\). Do đó, \(c = 1\). - Điểm \((-1, 0)\) cũng nằm trên đồ thị hàm số. Điều này cho thấy \(f(-1) = 0\). Thay vào phương trình hàm số, ta có: \[ f(-1) = a(-1)^2 + b(-1) + c = a - b + c = 0 \] Biết rằng \(c = 1\), ta thay vào: \[ a - b + 1 = 0 \] \[ a - b = -1 \quad \text{(1)} \] - Điểm \((1, 4)\) cũng nằm trên đồ thị hàm số. Điều này cho thấy \(f(1) = 4\). Thay vào phương trình hàm số, ta có: \[ f(1) = a(1)^2 + b(1) + c = a + b + c = 4 \] Biết rằng \(c = 1\), ta thay vào: \[ a + b + 1 = 4 \] \[ a + b = 3 \quad \text{(2)} \] Bước 2: Giải hệ phương trình để tìm \(a\) và \(b\). Ta có hai phương trình: \[ a - b = -1 \quad \text{(1)} \] \[ a + b = 3 \quad \text{(2)} \] Cộng hai phương trình lại: \[ (a - b) + (a + b) = -1 + 3 \] \[ 2a = 2 \] \[ a = 1 \] Thay \(a = 1\) vào phương trình (2): \[ 1 + b = 3 \] \[ b = 2 \] Bước 3: Tính giá trị của biểu thức \(T = a + 2b + 3c\). \[ T = 1 + 2(2) + 3(1) \] \[ T = 1 + 4 + 3 \] \[ T = 8 \] Vậy giá trị của biểu thức \(T\) là \(8\).