05/01/2025
Giúp mik vs săp đi hco rồi

 0
0
Làm sao để có câu trả lời hay nhất?
- Luôn có GIẢI THÍCH các bước giải
- Không copy câu trả lời của Timi
- Không sao chép trên mạng
- Không spam câu trả lời để nhận điểm
- Spam sẽ bị khóa tài khoản



05/01/2025
 0
0
05/01/2025
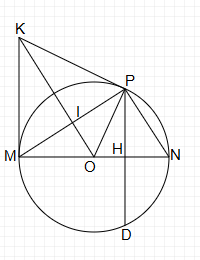
a, Vì P thuộc đường tròn đường kính MN nên
Xét
+)
+)
b, Vì KM và KP là các tiếp tuyến của (O) nên KM=KP
Mà OM=OP
Do đó OK là đường trung trực của MP
Ta có:
 0
0
05/01/2025
Trương Huyền a) Tính độ dài MN, MH nếu MP = 8 cm, NP = 6 cm.
- Độ dài MN:
- Do điểm P thuộc đường tròn (O; R), mà MN là đường kính của đường tròn, nên ta có:
- MN=MP+NP=8 cm+6 cm=14 cmMN = MP + NP = 8 \, \text{cm} + 6 \, \text{cm} = 14 \, \text{cm}MN=MP+NP=8cm+6cm=14cm
- Độ dài MH:
- Ta có tam giác vuông MNP với đường cao PH. Sử dụng định lý Pythagoras trong tam giác vuông MNP, ta có thể tính được MH, vì PH là đường cao từ P xuống cạnh MN.
- Để tính MH, ta cần biết thông tin thêm về tam giác vuông MNP hoặc một số thuộc tính hình học khác. Vì không có thông tin rõ ràng về góc, ta sẽ phải dựa vào các thuộc tính của tam giác vuông và đường tròn (O; R) để tính toán. Tuy nhiên, nếu bài toán yêu cầu cách tính chi tiết hơn, ta sẽ cần có thêm thông tin về các góc hay tỉ số giữa các đoạn thẳng.
b) Chứng minh bốn điểm H, P, K, F cùng thuộc một đường tròn và DF là tiếp tuyến của (O; R).
- Chứng minh bốn điểm H, P, K, F cùng thuộc một đường tròn:
- Để chứng minh bốn điểm H, P, K, F đồng thuộc một đường tròn, ta sử dụng tính chất của các điểm đồng thuộc một đường tròn:
- Từ cấu trúc bài toán, các điểm H, P, K, F có liên quan đến các tiếp tuyến và giao điểm của các đường thẳng cắt nhau tại các điểm trên đường tròn, vì vậy ta sẽ chứng minh tính chất này qua việc chỉ ra các tính chất đồng giác hoặc đồng hồ.
- Chứng minh DF là tiếp tuyến của (O; R):
- Để chứng minh DF là tiếp tuyến, ta cần chỉ ra rằng DF vuông góc với bán kính OD tại điểm D. Nếu DF là tiếp tuyến tại D, theo định lý tiếp tuyến, ta có:
- DF⊥ODDF \perp ODDF⊥OD
- Điều này có thể chứng minh bằng cách sử dụng các tính chất của tiếp tuyến và đường tròn, kết hợp với các giao điểm và các điểm liên quan trong bài toán.
Vì bài toán có sự kết hợp giữa các hình học phẳng và tính chất tiếp tuyến, nếu cần thiết, ta có thể dùng thêm các định lý như định lý tiếp tuyến, định lý giao điểm, hoặc các hệ quả từ định lý Pythagoras và các tỉ số trong tam giác vuông để hoàn thiện các chứng minh này.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
3 giờ trước
3 giờ trước
Top thành viên trả lời



 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




