Bocicioncduovc

Câu 2. Trước hết, ta cần tìm vị trí của chất điểm A sau 25 giây (vì B xuất phát chậm hơn 10 giây và đuổi kịp A sau 15 giây nữa, tức là sau tổng cộng 25 giây kể từ khi A bắt đầu chuyển động). Vận tốc của A theo thời gian là: \[ v_A(t) = \frac{1}{100}t^2 + \frac{13}{30}t \] Quãng đường mà A đã đi được sau 25 giây là: \[ s_A = \int_{0}^{25} v_A(t) \, dt = \int_{0}^{25} \left( \frac{1}{100}t^2 + \frac{13}{30}t \right) \, dt \] \[ s_A = \left[ \frac{1}{300}t^3 + \frac{13}{60}t^2 \right]_{0}^{25} \] \[ s_A = \left( \frac{1}{300}(25)^3 + \frac{13}{60}(25)^2 \right) - \left( \frac{1}{300}(0)^3 + \frac{13}{60}(0)^2 \right) \] \[ s_A = \frac{1}{300}(15625) + \frac{13}{60}(625) \] \[ s_A = \frac{15625}{300} + \frac{8125}{60} \] \[ s_A = \frac{15625}{300} + \frac{40625}{300} \] \[ s_A = \frac{56250}{300} \] \[ s_A = 187.5 \text{ m} \] Bây giờ, ta cần tìm vận tốc của B sau 15 giây. Vì B có gia tốc là \(a\) và xuất phát từ trạng thái nghỉ, vận tốc của B sau 15 giây là: \[ v_B = at \] \[ v_B = a \cdot 15 \] \[ v_B = 15a \] Quãng đường mà B đã đi được sau 15 giây là: \[ s_B = \frac{1}{2}at^2 \] \[ s_B = \frac{1}{2}a(15)^2 \] \[ s_B = \frac{1}{2}a \cdot 225 \] \[ s_B = 112.5a \] Vì B đuổi kịp A sau 15 giây, quãng đường B đi được phải bằng quãng đường A đi được: \[ s_B = s_A \] \[ 112.5a = 187.5 \] \[ a = \frac{187.5}{112.5} \] \[ a = 1.6667 \text{ m/s}^2 \] Vận tốc của B khi đuổi kịp A là: \[ v_B = 15a \] \[ v_B = 15 \cdot 1.6667 \] \[ v_B = 25 \text{ m/s} \] Đáp số: Vận tốc của B khi đuổi kịp A là 25 m/s. Câu 3. Để tính quãng đường S người đó chạy được trong 1 giờ 30 phút kể từ lúc bắt đầu chạy, ta thực hiện các bước sau: 1. Xác định phương trình của đường parabol: Vì đồ thị là một phần của đường parabol với đỉnh \( l(1;5) \) và trục đối xứng song song với trục tung Ov, ta có thể viết phương trình của đường parabol dưới dạng: \[ v = a(t - 1)^2 + 5 \] Để xác định giá trị của \( a \), ta cần biết thêm một điểm trên đồ thị. Giả sử ta biết thêm một điểm khác trên đồ thị, ví dụ \( (0, v_0) \). Ta sẽ thay vào phương trình để tìm \( a \). 2. Tìm giá trị của \( a \): Giả sử ta biết thêm điểm \( (0, 3) \) (tức là khi \( t = 0 \), \( v = 3 \)). Thay vào phương trình: \[ 3 = a(0 - 1)^2 + 5 \] \[ 3 = a + 5 \] \[ a = 3 - 5 \] \[ a = -2 \] Vậy phương trình của đường parabol là: \[ v = -2(t - 1)^2 + 5 \] 3. Tính quãng đường S người đó chạy được trong 1 giờ 30 phút: Quãng đường S người đó chạy được trong 1 giờ 30 phút (tức là \( t = 1.5 \)) là: \[ S = \int_{0}^{1.5} v(t) \, dt \] \[ S = \int_{0}^{1.5} (-2(t - 1)^2 + 5) \, dt \] Ta thực hiện phép tích phân: \[ S = \left[ -\frac{2}{3}(t - 1)^3 + 5t \right]_{0}^{1.5} \] \[ S = \left( -\frac{2}{3}(1.5 - 1)^3 + 5 \cdot 1.5 \right) - \left( -\frac{2}{3}(0 - 1)^3 + 5 \cdot 0 \right) \] \[ S = \left( -\frac{2}{3}(0.5)^3 + 7.5 \right) - \left( -\frac{2}{3}(-1)^3 \right) \] \[ S = \left( -\frac{2}{3} \cdot 0.125 + 7.5 \right) - \left( -\frac{2}{3} \cdot (-1) \right) \] \[ S = \left( -\frac{2}{3} \cdot 0.125 + 7.5 \right) - \left( \frac{2}{3} \right) \] \[ S = \left( -\frac{0.25}{3} + 7.5 \right) - \left( \frac{2}{3} \right) \] \[ S = \left( -0.0833 + 7.5 \right) - 0.6667 \] \[ S = 7.4167 - 0.6667 \] \[ S = 6.75 \] Vậy quãng đường S người đó chạy được trong 1 giờ 30 phút là 6.75 km. Câu 4. Để tìm phương trình của mặt phẳng $(Q)$ đi qua hai điểm $A(2;4;1)$ và $B(-1;1;3)$ và vuông góc với mặt phẳng $(P): x - 3y + 2z - 5 = 0$, ta thực hiện các bước sau: 1. Tìm vectơ pháp tuyến của mặt phẳng $(P)$: Mặt phẳng $(P)$ có phương trình $x - 3y + 2z - 5 = 0$. Vectơ pháp tuyến của $(P)$ là $\vec{n}_P = (1, -3, 2)$. 2. Tìm vectơ $\overrightarrow{AB}$: Điểm $A(2;4;1)$ và điểm $B(-1;1;3)$, ta có: \[ \overrightarrow{AB} = B - A = (-1 - 2, 1 - 4, 3 - 1) = (-3, -3, 2) \] 3. Tìm vectơ pháp tuyến của mặt phẳng $(Q)$: Mặt phẳng $(Q)$ đi qua hai điểm $A$ và $B$ và vuông góc với mặt phẳng $(P)$. Do đó, vectơ pháp tuyến của $(Q)$ sẽ vuông góc với cả $\vec{n}_P$ và $\overrightarrow{AB}$. Ta tính tích có hướng của hai vectơ này: \[ \vec{n}_Q = \vec{n}_P \times \overrightarrow{AB} \] \[ \vec{n}_Q = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & -3 & 2 \\ -3 & -3 & 2 \end{vmatrix} = \mathbf{i}((-3)(2) - (2)(-3)) - \mathbf{j}((1)(2) - (2)(-3)) + \mathbf{k}((1)(-3) - (-3)(-3)) \] \[ = \mathbf{i}( -6 + 6 ) - \mathbf{j}( 2 + 6 ) + \mathbf{k}( -3 - 9 ) \] \[ = \mathbf{i}(0) - \mathbf{j}(8) + \mathbf{k}(-12) \] \[ = (0, -8, -12) \] Ta có vectơ pháp tuyến của $(Q)$ là $\vec{n}_Q = (0, -8, -12)$. 4. Viết phương trình mặt phẳng $(Q)$: Mặt phẳng $(Q)$ có dạng $ax + by + cz - 11 = 0$. Với vectơ pháp tuyến $\vec{n}_Q = (0, -8, -12)$, ta có: \[ 0x - 8y - 12z - 11 = 0 \] Điều chỉnh để phù hợp với dạng $ax + by + cz - 11 = 0$, ta có: \[ 0x - 8y - 12z - 11 = 0 \] Do đó, $a = 0$, $b = -8$, $c = -12$. 5. Tính giá trị của $a + b + c$: \[ a + b + c = 0 + (-8) + (-12) = -20 \] Vậy giá trị của $a + b + c$ là $\boxed{-20}$. Câu 5. Để tính diện tích phần còn lại của mảnh đất hình chữ nhật ABCD sau khi trồng hoa vào phần giới hạn bởi cạnh AB, CD, đường trung bình MN và đường cong hình sin, chúng ta sẽ thực hiện các bước sau: 1. Tính diện tích toàn bộ mảnh đất hình chữ nhật ABCD: Diện tích hình chữ nhật ABCD là: \[ S_{ABCD} = AB \times AD = 2\pi \times 2 = 4\pi \text{ (m}^2\text{)} \] 2. Tính diện tích phần đất được tô màu đen: Phần đất được tô màu đen giới hạn bởi cạnh AB, CD, đường trung bình MN và đường cong hình sin. Đường trung bình MN chia mảnh đất thành hai phần bằng nhau, mỗi phần có chiều dài là \(\pi\) và chiều rộng là 2. Diện tích phần đất được tô màu đen là: \[ S_{đất tô màu} = \int_{0}^{2\pi} \sin(x) \, dx \] Ta tính tích phân: \[ \int_{0}^{2\pi} \sin(x) \, dx = -\cos(x) \Big|_{0}^{2\pi} = -\cos(2\pi) + \cos(0) = -1 + 1 = 0 \] Do đó, diện tích phần đất được tô màu đen là 0 (vì tích phân của sin(x) trên đoạn [0, 2π] là 0). 3. Tính diện tích phần còn lại: Diện tích phần còn lại là diện tích toàn bộ mảnh đất trừ đi diện tích phần đất được tô màu đen: \[ S_{còn lại} = S_{ABCD} - S_{đất tô màu} = 4\pi - 0 = 4\pi \text{ (m}^2\text{)} \] Vậy diện tích phần còn lại là: \[ \boxed{4\pi \text{ (m}^2\text{)}} \] Câu 6. Để tìm giá trị của \( x \) sao cho doanh thu là cao nhất, ta thực hiện các bước sau: 1. Tìm hàm doanh thu \( T(x) \) Ta biết rằng tốc độ thay đổi doanh thu \( T'(x) = -20x + 300 \). Để tìm hàm doanh thu \( T(x) \), ta tích phân \( T'(x) \): \[ T(x) = \int (-20x + 300) \, dx = -10x^2 + 300x + C \] Trong đó \( C \) là hằng số tích phân. 2. Xác định hằng số \( C \) Theo đề bài, nếu tăng giá thuê mỗi gian hàng thêm 10 triệu đồng thì doanh thu là 12 000 triệu đồng. 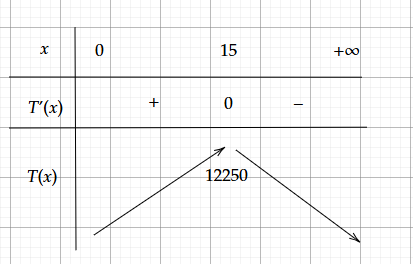Do đó, ta có: \[ T(10) = 12000 \] Thay vào phương trình \( T(x) \): \[ -10(10)^2 + 300(10) + C = 12000 \] \[ -1000 + 3000 + C = 12000 \] \[ 2000 + C = 12000 \] \[ C = 10000 \] Vậy hàm doanh thu là: \[ T(x) = -10x^2 + 300x + 10000 \] 3. Tìm giá trị của \( x \) để doanh thu là cao nhất Để tìm giá trị của \( x \) sao cho doanh thu là cao nhất, ta tìm điểm cực đại của hàm số \( T(x) \). Ta tính đạo hàm của \( T(x) \) và đặt nó bằng 0: \[ T'(x) = -20x + 300 \] \[ -20x + 300 = 0 \] \[ 20x = 300 \] \[ x = 15 \] Để kiểm tra xem \( x = 15 \) là điểm cực đại, ta tính đạo hàm bậc hai của \( T(x) \): \[ T''(x) = -20 \] Vì \( T''(x) < 0 \), nên \( x = 15 \) là điểm cực đại của hàm số \( T(x) \). Vậy giá trị của \( x \) để doanh thu là cao nhất là \( x = 15 \). Đáp số: \( x = 15 \)