Giúp mình với!

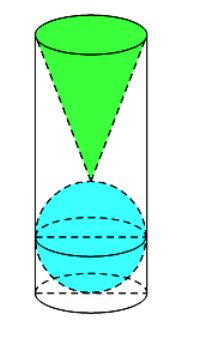
Bài 19. Gọi bán kính của cốc nước là R, chiều cao của cốc nước là H, thể tích của cốc nước là V1, thể tích của viên bi là V2, thể tích của hình nón là V3, thể tích của phần nước tràn ra là V4. Theo đề bài ta có: H = 3 x 2R = 6R V1 = πR^2 x H = πR^2 x 6R = 6πR^3 V2 = 4πR^3 : 3 V3 = πR^2 x R : 3 = πR^3 : 3 V4 = V2 + V3 = 4πR^3 : 3 + πR^3 : 3 = 5πR^3 : 3 Thể tích của lượng nước còn lại trong cốc là: V1 - V4 = 6πR^3 - 5πR^3 : 3 = 13πR^3 : 3 Tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu là: (13πR^3 : 3) : (6πR^3) = 13 : 18 Đáp số: 13 : 18 Bài 20. Gọi bán kính của hình trụ và hình nón là r (cm), đường sinh của hình trụ và hình nón là l (cm). Theo đề bài ta có: l = 2r Thể tích toàn bộ khối đồ chơi là: \[ V_{tổng} = V_{trụ} + V_{nón} \] \[ V_{tổng} = S_{đáy} \times h_{trụ} + \frac{1}{3} \times S_{đáy} \times h_{nón} \] \[ V_{tổng} = S_{đáy} \times (h_{trụ} + \frac{1}{3} \times h_{nón}) \] \[ V_{tổng} = S_{đáy} \times (\frac{3}{3} \times h_{trụ} + \frac{1}{3} \times h_{nón}) \] \[ V_{tổng} = S_{đáy} \times \frac{1}{3} \times (3 \times h_{trụ} + h_{nón}) \] \[ V_{tổng} = S_{đáy} \times \frac{1}{3} \times (3 \times 2r + 2r) \] \[ V_{tổng} = S_{đáy} \times \frac{1}{3} \times 8r \] \[ V_{tổng} = \frac{8}{3} \times V_{trụ} \] \[ V_{trụ} = \frac{3}{8} \times V_{tổng} \] \[ V_{trụ} = \frac{3}{8} \times 50 = 18,75 ~cm^3 \] Đáp số: 18,75 cm³ Bài 21. Chiều cao chất lỏng ban đầu là $\frac{h}{24}$. Thể tích chất lỏng ban đầu là $\frac{1}{24}$ thể tích của hình trụ. Khi lật ngược dụng cụ, thể tích chất lỏng không đổi nên thể tích chất lỏng chiếm $\frac{1}{24}$ thể tích của hình nón. Thể tích của hình nón là $\frac{1}{3}$ thể tích của hình trụ nên thể tích chất lỏng chiếm $\frac{1}{24} \times \frac{1}{3} = \frac{1}{72}$ thể tích của hình trụ. Gọi chiều cao chất lỏng trong hình nón là $h'$. Ta có: $\frac{1}{72}$ thể tích của hình trụ = $\frac{1}{72}$ $\pi r^2 h = \frac{1}{3} \pi r^2 h'$ Từ đó ta có: $\frac{1}{72} h = \frac{1}{3} h'$ $h' = \frac{1}{72} \times 3 = \frac{h}{24}$ Đáp số: $\frac{h}{24}$ Bài 22. Để tính thể tích của khối bê tông, chúng ta sẽ tính thể tích của từng phần riêng lẻ và sau đó trừ đi thể tích của phần rỗng. Chiều cao của khối bê tông là $h = 1,5m$. 1. Phần dưới có dạng hình trụ: Bán kính đáy của phần này là $R = 1m$, chiều cao của phần này là $\frac{1}{3}h = \frac{1}{3} \times 1,5 = 0,5m$. Thể tích của phần này là: \[ V_{trụ} = \pi R^2 h_{trụ} = \pi \times 1^2 \times 0,5 = 0,5\pi \text{ m}^3 \] 2. Phần trên có dạng hình nón cụt: Bán kính đáy lớn của phần này là $R = 1m$, bán kính đáy nhỏ của phần này là $\frac{1}{2}R = 0,5m$, chiều cao của phần này là $\frac{1}{3}h = 0,5m$. Thể tích của phần này là: \[ V_{nón-cụt} = \frac{1}{3}\pi h_{nón-cụt}(R_1^2 + R_1R_2 + R_2^2) \] \[ V_{nón-cụt} = \frac{1}{3}\pi \times 0,5 \times (1^2 + 1 \times 0,5 + 0,5^2) \] \[ V_{nón-cụt} = \frac{1}{3}\pi \times 0,5 \times (1 + 0,5 + 0,25) \] \[ V_{nón-cụt} = \frac{1}{3}\pi \times 0,5 \times 1,75 \] \[ V_{nón-cụt} = \frac{1}{3}\pi \times 0,875 \] \[ V_{nón-cụt} = 0,291666667\pi \text{ m}^3 \] 3. Phần ở giữa rỗng có dạng hình trụ: Bán kính đáy của phần này là $\frac{1}{4}R = 0,25m$, chiều cao của phần này là $\frac{1}{3}h = 0,5m$. Thể tích của phần này là: \[ V_{rỗng} = \pi R_{rỗng}^2 h_{rỗng} = \pi \times 0,25^2 \times 0,5 = \pi \times 0,0625 \times 0,5 = 0,03125\pi \text{ m}^3 \] 4. Tổng thể tích của khối bê tông: \[ V_{tổng} = V_{trụ} + V_{nón-cụt} - V_{rỗng} \] \[ V_{tổng} = 0,5\pi + 0,291666667\pi - 0,03125\pi \] \[ V_{tổng} = (0,5 + 0,291666667 - 0,03125)\pi \] \[ V_{tổng} = 0,760416667\pi \text{ m}^3 \] Vậy thể tích của khối bê tông là $0,760416667\pi \text{ m}^3$.