Vbjhfxkxixdoo

Câu 1. Để giải phương trình $27^{2x-3} = \left(\frac{1}{3}\right)^{x^2 + 2}$, ta thực hiện các bước sau: Bước 1: Viết lại các cơ số dưới dạng cùng cơ số. Ta biết rằng $27 = 3^3$ và $\frac{1}{3} = 3^{-1}$. Do đó, ta có: \[ 27^{2x-3} = (3^3)^{2x-3} = 3^{3(2x-3)} = 3^{6x - 9} \] \[ \left(\frac{1}{3}\right)^{x^2 + 2} = (3^{-1})^{x^2 + 2} = 3^{-(x^2 + 2)} = 3^{-x^2 - 2} \] Bước 2: Bằng cách so sánh hai vế của phương trình, ta có: \[ 3^{6x - 9} = 3^{-x^2 - 2} \] Bước 3: Vì hai lũy thừa có cùng cơ số, ta có thể so sánh các mũ của chúng: \[ 6x - 9 = -x^2 - 2 \] Bước 4: Chuyển tất cả các hạng tử về một vế để tạo thành phương trình bậc hai: \[ x^2 + 6x - 9 + 2 = 0 \] \[ x^2 + 6x - 7 = 0 \] Bước 5: Giải phương trình bậc hai này bằng cách phân tích thành nhân tử: \[ x^2 + 6x - 7 = (x + 7)(x - 1) = 0 \] Bước 6: Tìm nghiệm của phương trình: \[ x + 7 = 0 \quad \text{hoặc} \quad x - 1 = 0 \] \[ x = -7 \quad \text{hoặc} \quad x = 1 \] Vậy nghiệm của phương trình là: \[ x = -7 \quad \text{hoặc} \quad x = 1 \] Câu 2. Để tìm thời gian để vi khuẩn tăng gấp đôi số vi khuẩn ban đầu, chúng ta sẽ thực hiện các bước sau: 1. Xác định các thông số ban đầu: - Số lượng vi khuẩn ban đầu \(A = 100\) con. - Sau 5 giờ, số lượng vi khuẩn là 300 con. 2. Áp dụng công thức tăng trưởng: \[ S = A \cdot e^{rt} \] Thay \(S = 300\), \(A = 100\), và \(t = 5\) vào công thức: \[ 300 = 100 \cdot e^{5r} \] 3. Giải phương trình để tìm \(r\): \[ 3 = e^{5r} \] Lấy logarit tự nhiên hai vế: \[ \ln(3) = \ln(e^{5r}) \] \[ \ln(3) = 5r \] \[ r = \frac{\ln(3)}{5} \] 4. Tìm thời gian để vi khuẩn tăng gấp đôi: Gấp đôi số vi khuẩn ban đầu tức là \(S = 200\): \[ 200 = 100 \cdot e^{rt} \] \[ 2 = e^{rt} \] Thay \(r = \frac{\ln(3)}{5}\) vào: \[ 2 = e^{\left(\frac{\ln(3)}{5}\right)t} \] Lấy logarit tự nhiên hai vế: \[ \ln(2) = \ln\left(e^{\left(\frac{\ln(3)}{5}\right)t}\right) \] \[ \ln(2) = \left(\frac{\ln(3)}{5}\right)t \] \[ t = \frac{5 \ln(2)}{\ln(3)} \] 5. Kết luận: Thời gian để vi khuẩn tăng gấp đôi số vi khuẩn ban đầu là: \[ t = \frac{5 \ln(2)}{\ln(3)} \] Đáp số: \( t = \frac{5 \ln(2)}{\ln(3)} \) giờ. Câu 3. Để chứng minh $(SBD) \perp (SAC)$, ta sẽ sử dụng tính chất của đường thẳng vuông góc với mặt phẳng và mặt phẳng vuông góc với mặt phẳng khác. Bước 1: Xác định các đường thẳng và mặt phẳng liên quan. - Đáy ABCD là hình vuông, do đó AC và BD là hai đường chéo của hình vuông. - SA vuông góc với mặt phẳng (ABCD). Bước 2: Chứng minh SA vuông góc với BD. - Vì SA vuông góc với mặt phẳng (ABCD), nên SA vuông góc với mọi đường thẳng nằm trong mặt phẳng (ABCD), bao gồm cả BD. Bước 3: Chứng minh AC vuông góc với BD. - Trong hình vuông ABCD, đường chéo AC vuông góc với đường chéo BD. Bước 4: Kết luận BD vuông góc với mặt phẳng (SAC). - Ta đã chứng minh SA vuông góc với BD và AC vuông góc với BD. - Do đó, BD vuông góc với hai đường thẳng SA và AC, nằm trong mặt phẳng (SAC). - Theo tính chất của đường thẳng vuông góc với mặt phẳng, nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng đó thì đường thẳng đó vuông góc với mặt phẳng đó. - Vậy BD vuông góc với mặt phẳng (SAC). Bước 5: Kết luận mặt phẳng (SBD) vuông góc với mặt phẳng (SAC). - Vì BD nằm trong mặt phẳng (SBD) và BD vuông góc với mặt phẳng (SAC), theo tính chất của mặt phẳng vuông góc với mặt phẳng khác, nếu một đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia thì mặt phẳng này vuông góc với mặt phẳng kia. - Vậy mặt phẳng (SBD) vuông góc với mặt phẳng (SAC). Đáp số: $(SBD) \perp (SAC)$. Câu 4. 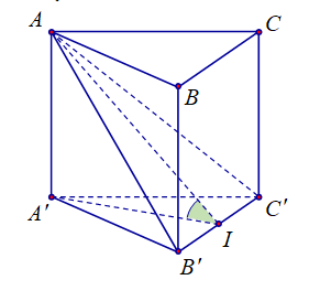Để tính góc giữa hai mặt phẳng $(AB^\prime C^\prime)$ và $(A^\prime B^\prime C^\prime)$ trong lăng trụ đều ABC.A'B'C', ta thực hiện các bước sau: 1. Xác định giao tuyến của hai mặt phẳng: - Mặt phẳng $(AB^\prime C^\prime)$ và $(A^\prime B^\prime C^\prime)$ chung giao tuyến là $B^\prime C^\prime$. 2. Xác định đường vuông góc hạ từ điểm A xuống giao tuyến $B^\prime C^\prime$: - Gọi H là trung điểm của $B^\prime C^\prime$, ta hạ đường thẳng AH vuông góc với $B^\prime C^\prime$. 3. Xác định đường vuông góc hạ từ điểm A' xuống giao tuyến $B^\prime C^\prime$: - Gọi H' là trung điểm của $B^\prime C^\prime$, ta hạ đường thẳng A'H' vuông góc với $B^\prime C^\prime$. 4. Xác định góc giữa hai mặt phẳng: - Góc giữa hai mặt phẳng $(AB^\prime C^\prime)$ và $(A^\prime B^\prime C^\prime)$ là góc giữa hai đường thẳng AH và A'H'. 5. Tính toán: - Vì lăng trụ đều nên tam giác $AB^\prime C^\prime$ và $A^\prime B^\prime C^\prime$ đều là tam giác đều. - Độ dài cạnh $B^\prime C^\prime$ là 2a. - Độ dài đoạn thẳng AH và A'H' là $\frac{\sqrt{3}}{2} \times 2a = a\sqrt{3}$. - Độ dài đoạn thẳng AA' là a. 6. Áp dụng công thức tính góc giữa hai đường thẳng: - Ta có $\cos(\angle HAH') = \frac{AA'}{AH} = \frac{a}{a\sqrt{3}} = \frac{1}{\sqrt{3}}$. - Vậy góc $\angle HAH'$ là $\arccos\left(\frac{1}{\sqrt{3}}\right)$. Kết luận: Góc giữa hai mặt phẳng $(AB^\prime C^\prime)$ và $(A^\prime B^\prime C^\prime)$ là $\arccos\left(\frac{1}{\sqrt{3}}\right)$. Câu 5. Để tính khoảng cách từ điểm A đến mặt phẳng (SBC), ta thực hiện các bước sau: 1. Tìm diện tích của tam giác SBC: Vì SA vuông góc với mặt phẳng (ABC), nên SA cũng vuông góc với BC. Ta tính diện tích tam giác SBC bằng công thức diện tích tam giác có hai cạnh và đường cao: \[ S_{SBC} = \frac{1}{2} \times BC \times SA = \frac{1}{2} \times a \times a = \frac{a^2}{2} \] 2. Tính thể tích của khối chóp SABC: Thể tích của khối chóp SABC được tính bằng công thức: \[ V_{SABC} = \frac{1}{3} \times S_{ABC} \times SA \] Diện tích tam giác đều ABC là: \[ S_{ABC} = \frac{\sqrt{3}}{4} a^2 \] Vậy thể tích của khối chóp SABC là: \[ V_{SABC} = \frac{1}{3} \times \frac{\sqrt{3}}{4} a^2 \times a = \frac{\sqrt{3}}{12} a^3 \] 3. Tính khoảng cách từ điểm A đến mặt phẳng (SBC): Gọi khoảng cách từ điểm A đến mặt phẳng (SBC) là h. Thể tích của khối chóp SABC cũng có thể được tính bằng: \[ V_{SABC} = \frac{1}{3} \times S_{SBC} \times h \] Thay vào giá trị đã biết: \[ \frac{\sqrt{3}}{12} a^3 = \frac{1}{3} \times \frac{a^2}{2} \times h \] Giải phương trình này để tìm h: \[ \frac{\sqrt{3}}{12} a^3 = \frac{a^2}{6} \times h \] \[ h = \frac{\sqrt{3}}{12} a^3 \times \frac{6}{a^2} = \frac{\sqrt{3}}{2} a \] Vậy khoảng cách từ điểm A đến mặt phẳng (SBC) là: \[ \boxed{\frac{\sqrt{3}}{2} a} \] Câu 6. Trước tiên, ta xác định các thông tin đã cho và vẽ sơ đồ hình học để dễ dàng hơn trong việc giải bài toán. - Đáy ABCD là hình thoi cạnh bằng a, tâm O, $\widehat{ABC}=120^0$. - SA = SB = SD = a. Bước 1: Xác định khoảng cách giữa hai đường thẳng BD và SC Ta thấy rằng, khoảng cách giữa hai đường thẳng BD và SC sẽ là khoảng cách từ điểm C đến mặt phẳng (SBD). Bước 2: Tìm diện tích của tam giác SBD Ta biết rằng, tam giác SBD là tam giác đều cạnh a (vì SA = SB = SD = a). Diện tích của tam giác đều cạnh a là: \[ S_{SBD} = \frac{\sqrt{3}}{4} a^2 \] Bước 3: Tìm thể tích của khối chóp SABCD Khối chóp SABCD có đáy là hình thoi ABCD và đỉnh S. Ta tính diện tích đáy ABCD: Diện tích của hình thoi ABCD là: \[ S_{ABCD} = a^2 \sin(120^\circ) = a^2 \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{2} a^2 \] Chiều cao SO của khối chóp SABCD hạ từ đỉnh S vuông góc xuống đáy ABCD. Ta có thể tính chiều cao SO bằng cách sử dụng công thức tính thể tích của khối chóp: \[ V_{SABCD} = \frac{1}{3} \times S_{ABCD} \times SO \] Bước 4: Tính khoảng cách từ điểm C đến mặt phẳng (SBD) Khoảng cách từ điểm C đến mặt phẳng (SBD) là: \[ d(C, (SBD)) = \frac{3 \times V_{SABCD}}{S_{SBD}} \] Thay các giá trị đã tính vào: \[ V_{SABCD} = \frac{1}{3} \times \frac{\sqrt{3}}{2} a^2 \times SO \] \[ d(C, (SBD)) = \frac{3 \times \frac{1}{3} \times \frac{\sqrt{3}}{2} a^2 \times SO}{\frac{\sqrt{3}}{4} a^2} = \frac{\frac{\sqrt{3}}{2} a^2 \times SO}{\frac{\sqrt{3}}{4} a^2} = 2 \times SO \] Bước 5: Kết luận Khoảng cách giữa hai đường thẳng BD và SC là: \[ d(BD, SC) = 2 \times SO \] Để tính chính xác SO, ta cần thêm thông tin về chiều cao SO hoặc sử dụng các phương pháp khác để xác định SO. Tuy nhiên, dựa trên các thông tin đã cho và các bước trên, ta có thể kết luận rằng khoảng cách giữa hai đường thẳng BD và SC là: \[ d(BD, SC) = 2 \times SO \] Đáp số: Khoảng cách giữa hai đường thẳng BD và SC là \( 2 \times SO \).