ghidufncchhcvjjvfucnnv.

Câu 1. Để giải bài toán này, chúng ta sẽ thực hiện các bước sau: 1. Tìm tích phân của hàm số \( f(x) = mx + n \): \[ \int f(x) \, dx = \int (mx + n) \, dx = \frac{m}{2}x^2 + nx + C \] 2. Áp dụng giới hạn tích phân từ 0 đến 1: \[ \int_0^1 f(x) \, dx = \left[ \frac{m}{2}x^2 + nx \right]_0^1 = \left( \frac{m}{2}(1)^2 + n(1) \right) - \left( \frac{m}{2}(0)^2 + n(0) \right) = \frac{m}{2} + n \] Theo đề bài, ta có: \[ \frac{m}{2} + n = 8 \] 3. Áp dụng giới hạn tích phân từ 0 đến 2: \[ \int_0^2 f(x) \, dx = \left[ \frac{m}{2}x^2 + nx \right]_0^2 = \left( \frac{m}{2}(2)^2 + n(2) \right) - \left( \frac{m}{2}(0)^2 + n(0) \right) = 2m + 2n \] Theo đề bài, ta có: \[ 3 \cdot \int_0^2 f(x) \, dx = 3 \cdot (2m + 2n) = 8 \] Do đó: \[ 6m + 6n = 8 \quad \Rightarrow \quad m + n = \frac{8}{6} = \frac{4}{3} \] 4. Giải hệ phương trình: Ta có hai phương trình: \[ \begin{cases} \frac{m}{2} + n = 8 \\ m + n = \frac{4}{3} \end{cases} \] Từ phương trình thứ hai, ta có: \[ n = \frac{4}{3} - m \] Thay vào phương trình thứ nhất: \[ \frac{m}{2} + \left( \frac{4}{3} - m \right) = 8 \] Nhân cả hai vế với 6 để loại bỏ mẫu số: \[ 3m + 8 - 6m = 48 \quad \Rightarrow \quad -3m = 40 \quad \Rightarrow \quad m = -\frac{40}{3} \] Thay \( m = -\frac{40}{3} \) vào \( n = \frac{4}{3} - m \): \[ n = \frac{4}{3} - \left( -\frac{40}{3} \right) = \frac{4}{3} + \frac{40}{3} = \frac{44}{3} \] 5. Tính \( m + n \): \[ m + n = -\frac{40}{3} + \frac{44}{3} = \frac{4}{3} \] Vậy, giá trị của \( m + n \) là: \[ \boxed{\frac{4}{3}} \] Câu 2. Để tìm quãng đường ô tô di chuyển từ lúc hãm phanh đến khi dừng hẳn, ta cần tính khoảng thời gian mà ô tô mất để dừng lại và sau đó tính quãng đường đã đi được trong khoảng thời gian đó. Bước 1: Xác định thời điểm ô tô dừng hẳn - Ô tô dừng hẳn khi vận tốc \( v(t) = 0 \). Ta có: \[ v(t) = -36t + 18 \] Đặt \( v(t) = 0 \): \[ -36t + 18 = 0 \] \[ -36t = -18 \] \[ t = \frac{-18}{-36} \] \[ t = 0.5 \text{ giây} \] Bước 2: Tính quãng đường ô tô di chuyển trong khoảng thời gian từ lúc hãm phanh đến khi dừng hẳn - Quãng đường \( s \) được tính bằng tích của vận tốc trung bình và thời gian. Vận tốc ban đầu \( v_0 = 18 \text{ m/s} \) Vận tốc cuối cùng \( v_f = 0 \text{ m/s} \) Vận tốc trung bình \( v_{\text{tb}} \) là: \[ v_{\text{tb}} = \frac{v_0 + v_f}{2} = \frac{18 + 0}{2} = 9 \text{ m/s} \] Thời gian \( t = 0.5 \text{ giây} \) Quãng đường \( s \) là: \[ s = v_{\text{tb}} \times t = 9 \times 0.5 = 4.5 \text{ mét} \] Vậy, từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển 4.5 mét. Câu 3. Để tính tổng diện tích đáy trên và đáy dưới của khối tròn xoay, ta cần xác định diện tích của hai hình tròn đáy này. Diện tích của mỗi hình tròn đáy sẽ là diện tích của hình tròn có bán kính bằng giá trị của hàm số \( f(x) \) tại các điểm đầu mút của đoạn thẳng \( x = 0 \) và \( x = 4 \). Bước 1: Tính giá trị của hàm số \( f(x) \) tại \( x = 0 \) và \( x = 4 \): \[ f(0) = 0^2 - 4 \cdot 0 + 5 = 5 \] \[ f(4) = 4^2 - 4 \cdot 4 + 5 = 16 - 16 + 5 = 5 \] Bước 2: Xác định bán kính của các hình tròn đáy: - Bán kính của hình tròn đáy trên là \( r_1 = 5 \) - Bán kính của hình tròn đáy dưới là \( r_2 = 5 \) Bước 3: Tính diện tích của mỗi hình tròn đáy: \[ S_{đáy} = \pi r^2 \] Diện tích của mỗi hình tròn đáy là: \[ S_{đáy} = \pi \cdot 5^2 = 25\pi \] Bước 4: Tính tổng diện tích của hai hình tròn đáy: \[ S_{tổng} = 2 \cdot 25\pi = 50\pi \] Vậy tổng diện tích đáy trên và đáy dưới của khối tròn xoay là \( 50\pi \). Câu 4. Để giải bài toán này, chúng ta cần tìm điểm hạ cánh \( M(a, b, c) \) của máy bay trên mặt sân bay \( Oxy \). Mặt sân bay \( Oxy \) có phương trình \( z = 0 \). Bước 1: Xác định phương trình đường thẳng đi qua hai điểm \( A(5, 0, 5) \) và \( B(10, 10, 3) \). Phương trình tham số của đường thẳng đi qua hai điểm \( A \) và \( B \) là: \[ \begin{cases} x = 5 + t(10 - 5) \\ y = 0 + t(10 - 0) \\ z = 5 + t(3 - 5) \end{cases} \] \[ \begin{cases} x = 5 + 5t \\ y = 10t \\ z = 5 - 2t \end{cases} \] Bước 2: Tìm tọa độ điểm \( M(a, b, c) \) trên mặt sân bay \( Oxy \) (nghĩa là \( z = 0 \)). Thay \( z = 0 \) vào phương trình \( z = 5 - 2t \): \[ 5 - 2t = 0 \implies t = \frac{5}{2} = 2.5 \] Bước 3: Thay \( t = 2.5 \) vào phương trình tham số để tìm tọa độ của điểm \( M \): \[ \begin{cases} a = 5 + 5 \cdot 2.5 = 5 + 12.5 = 17.5 \\ b = 10 \cdot 2.5 = 25 \\ c = 5 - 2 \cdot 2.5 = 5 - 5 = 0 \end{cases} \] Bước 4: Tính giá trị của \( a + b - 2c \): \[ a + b - 2c = 17.5 + 25 - 2 \cdot 0 = 17.5 + 25 = 42.5 \] Vậy giá trị của \( a + b - 2c \) là \( 42.5 \). Đáp số: \( 42.5 \) Câu 5. Để tìm phương trình mặt phẳng (Q) đi qua hai điểm A và B và vuông góc với mặt phẳng (P), ta thực hiện các bước sau: 1. Tìm vectơ pháp tuyến của mặt phẳng (P): Mặt phẳng (P) có phương trình \(x - y + z - 4 = 0\). Vectơ pháp tuyến của (P) là \(\vec{n}_P = (1, -1, 1)\). 2. Tìm vectơ AB: Điểm A(1, 2, 0) và điểm B(3, 4, -2). \[ \vec{AB} = (3 - 1, 4 - 2, -2 - 0) = (2, 2, -2) \] 3. Tìm vectơ pháp tuyến của mặt phẳng (Q): Mặt phẳng (Q) đi qua hai điểm A và B và vuông góc với mặt phẳng (P). Do đó, vectơ pháp tuyến của (Q) sẽ vuông góc với cả \(\vec{n}_P\) và \(\vec{AB}\). Ta tính tích có hướng của hai vectơ này: \[ \vec{n}_Q = \vec{n}_P \times \vec{AB} \] \[ \vec{n}_Q = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & -1 & 1 \\ 2 & 2 & -2 \end{vmatrix} = \vec{i}((-1)(-2) - (1)(2)) - \vec{j}((1)(-2) - (1)(2)) + \vec{k}((1)(2) - (-1)(2)) \] \[ \vec{n}_Q = \vec{i}(2 - 2) - \vec{j}(-2 - 2) + \vec{k}(2 + 2) = \vec{i}(0) - \vec{j}(-4) + \vec{k}(4) = (0, 4, 4) \] Vậy vectơ pháp tuyến của mặt phẳng (Q) là \(\vec{n}_Q = (0, 4, 4)\). 4. Viết phương trình mặt phẳng (Q): Mặt phẳng (Q) đi qua điểm A(1, 2, 0) và có vectơ pháp tuyến \(\vec{n}_Q = (0, 4, 4)\). Phương trình mặt phẳng (Q) có dạng: \[ 0(x - 1) + 4(y - 2) + 4(z - 0) = 0 \] \[ 4y - 8 + 4z = 0 \] \[ 4y + 4z - 8 = 0 \] Chia cả phương trình cho 4 để đơn giản hóa: \[ y + z - 2 = 0 \] So sánh với phương trình đã cho \((Q): ax + by + cz + 2 = 0\), ta thấy \(a = 0\), \(b = 1\), \(c = 1\). 5. Tính \(T = a + b + c\): \[ T = 0 + 1 + 1 = 2 \] Vậy đáp án là \(T = 2\). Câu 6. 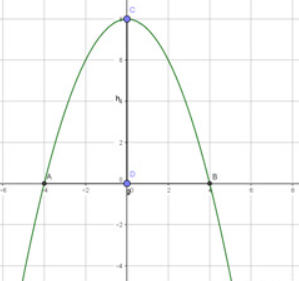Để tính diện tích mặt kính cần lắp vào vòm cửa có dạng hình parabol, chúng ta sẽ thực hiện các bước sau: 1. Xác định phương trình của parabol: - Vòm cửa có dạng hình parabol và cao 8m, rộng 8m. Ta chọn hệ tọa độ sao cho đỉnh parabol trùng với gốc tọa độ (0,0) và trục đối xứng là trục y. - Phương trình của parabol có dạng \( y = ax^2 \). 2. Xác định tham số \( a \): - Điểm (4, 8) thuộc parabol vì vòm cửa rộng 8m nên điểm này nằm ở phía bên phải đỉnh parabol. - Thay tọa độ điểm (4, 8) vào phương trình \( y = ax^2 \): \[ 8 = a \cdot 4^2 \implies 8 = 16a \implies a = \frac{8}{16} = \frac{1}{2} \] - Vậy phương trình của parabol là: \[ y = \frac{1}{2}x^2 \] 3. Tính diện tích mặt kính: - Diện tích mặt kính cần lắp vào là diện tích giữa hai đường thẳng \( x = -4 \) và \( x = 4 \) và parabol \( y = \frac{1}{2}x^2 \). - Diện tích này có thể tính bằng tích phân: \[ A = 2 \int_{0}^{4} \left( 8 - \frac{1}{2}x^2 \right) dx \] - Tính tích phân: \[ \int_{0}^{4} \left( 8 - \frac{1}{2}x^2 \right) dx = \left[ 8x - \frac{1}{6}x^3 \right]_{0}^{4} \] \[ = \left( 8 \cdot 4 - \frac{1}{6} \cdot 4^3 \right) - \left( 8 \cdot 0 - \frac{1}{6} \cdot 0^3 \right) \] \[ = 32 - \frac{64}{6} = 32 - \frac{32}{3} = \frac{96}{3} - \frac{32}{3} = \frac{64}{3} \] - Vậy diện tích một nửa là \( \frac{64}{3} \). Diện tích toàn bộ là: \[ A = 2 \times \frac{64}{3} = \frac{128}{3} \approx 42.7 \text{ m}^2 \] Đáp số: Diện tích mặt kính cần lắp vào là khoảng 42.7 m².