28/03/2025
Cho nửa đường tròn (O) đường kính AB. Trên cùng một nửa mặt phẳng chứa bờ AB, kẻ hai tiếp tuyến Ax, By của nửa đường tròn (0). Từ một điểm M trên nửa đường tròn kẻ tiếp tuyến tại M cắt Ax, By lần lượt...
Làm sao để có câu trả lời hay nhất?
- Luôn có GIẢI THÍCH các bước giải
- Không copy câu trả lời của Timi
- Không sao chép trên mạng
- Không spam câu trả lời để nhận điểm
- Spam sẽ bị khóa tài khoản



28/03/2025
 0
0
28/03/2025
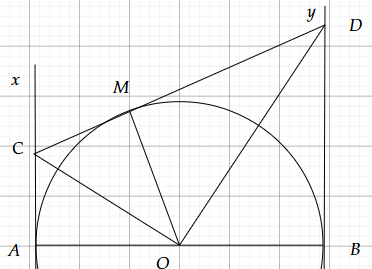
a)
CA, CM là tiếp tuyến của (O) ⟹
Xét tứ giác ACMO, có:
mà hai góc này ở vị trí đối nhau
⟹ Tứ giác ACMO nội tiếp
Xét
CO chung
AO=MO =R
CMTT ⟹
Có:
b)
Có:
Có:
⟹ Tam giác COD vuông tại O
Tam giác COD vuông tại O có đường cao OM, có:
 0
0
28/03/2025
Nhi NguyễnCâu a: Chứng minh tứ giác ACMO nội tiếp và AC + BD = CD
- Ta có AC và BD là hai tiếp tuyến của nửa đường tròn tại M, do đó OM là bán kính vuông góc với tiếp tuyến tại M, tức là OM ⊥ MC và OM ⊥ MD.
- Vì OM là đường kính của đường tròn ngoại tiếp nửa đường tròn, nên ∠MOC = 90° và ∠MOA = 90°.
- Do đó, tứ giác ACMO có bốn điểm cùng nằm trên một đường tròn, vì góc nội tiếp cùng chắn cung MA.
- Suy ra tứ giác ACMO nội tiếp.
Bây giờ, xét các tam giác đồng dạng:
- ΔMAC ∼ ΔMBD (góc chung tại M và góc đối đỉnh)
- Từ đây, ta có AC / BD = MC / MD
- Vì AC và BD là các tiếp tuyến từ A, B đến M, nên AC + BD = CD (tính chất tiếp tuyến cắt nhau).
Kết luận: Tứ giác ACMO nội tiếp và AC + BD = CD.
Câu b: Chứng minh rằng OM² = MC × MD
- Xét tam giác ΔOMC và ΔOMD, vì OM vuông góc với tiếp tuyến tại M nên ∠OMC = ∠OMD = 90°.
- Theo hệ thức lượng trong tam giác vuông, ta có:
- OM2=MC×MDOM² = MC × MDOM2=MC×MD
- Đây là một hệ thức đặc biệt trong tam giác vuông, chứng tỏ rằng tích của hai đoạn MC và MD bằng bình phương bán kính OM.
Kết luận: OM² = MC × MD.
Câu c: Chứng minh K là trung điểm của MH
- Kẻ MH ⊥ AB tại H, cắt CB tại K.
- Xét hai tam giác ΔMHC và ΔMHB, ta có:
- MH là đường cao chung
- ∠MHC = ∠MHB = 90°
- Do đó, MH là đường trung tuyến ứng với cạnh huyền của tam giác vuông MHC, nên K chính là trung điểm của MH.
Kết luận: K là trung điểm của MH.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
5 giờ trước
Top thành viên trả lời




 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




