Giải hộ mình câu này với các bạn

dinhnhanhlChắc chắn rồi, hãy cùng giải bài toán hình học này:

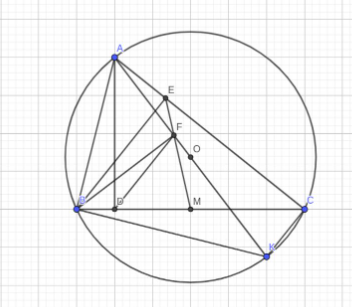
Câu 13: Cho đường tròn (O; R) và dây BC cố định không đi qua tâm. Gọi A là một điểm bất kỳ trên cung lớn BC sao cho tam giác ABC nhọn (AB < AC). Kẻ các đường cao AD, BE của tam giác ABC.

a) Chứng minh tứ giác AEFD nội tiếp.

Lời giải:

Xét tứ giác AEFD:

Ta có: ∠AFD = 90° (FD ⊥ AB)

Ta có: ∠AED = 90° (ED ⊥ AC)

Suy ra: ∠AFD + ∠AED = 90° + 90° = 180°

Kết luận:

Tứ giác AEFD có tổng hai góc đối diện bằng 180°, suy ra tứ giác AEFD nội tiếp.

b) Kẻ đường kính AK của đường tròn (O). Gọi F là hình chiếu của B trên AK. Chứng minh: ΔABD ~ ΔAKE và DF ⊥ AC.

Lời giải:

Chứng minh ΔABD ~ ΔAKE:

Ta có: ∠ADB = ∠AEK = 90°

Ta có: ∠ABD = ∠AKE (cùng chắn cung AC)

Suy ra: ΔABD ~ ΔAKE (g.g)

Chứng minh DF ⊥ AC:

Ta có: ∠AFE = ∠ADE = 90° (tứ giác AEFD nội tiếp)

Suy ra: ∠AFE = ∠AKE = 90°

Suy ra: EF // KE (cùng vuông góc với AK)

Mà KE ⊥ AB (BF ⊥ AK)

Suy ra: EF ⊥ AB

Lại có: ∠AFE = ∠ADE = 90° (tứ giác AEFD nội tiếp)

Suy ra: ∠AFE = ∠ADE = 90°

Suy ra: AEFD nội tiếp đường tròn đường kính AE.

Suy ra: ∠ADF = ∠AEF (cùng chắn cung AF)

Suy ra: ∠ADF = ∠AEF = 90°

Suy ra: DF ⊥ AC.

Kết luận:

a) Tứ giác AEFD nội tiếp.

b) ΔABD ~ ΔAKE và DF ⊥ AC.

Chắc chắn rồi, dưới đây là lời giải chi tiết cho bài toán hình học bạn cung cấp:

Bài toán: Cho đường tròn (O; R) và dây BC cố định không đi qua tâm. Gọi A là một điểm bất kỳ trên cung lớn BC sao cho tam giác ABC nhọn (AB < AC). Kẻ các đường cao AD, BE của tam giác ABC.

a) Chứng minh tứ giác AEFD nội tiếp.

b) Kẻ đường kính AK của đường tròn (O). Gọi F là hình chiếu của D trên AK. Chứng minh: ΔABD ~ ΔAKC và DF ⊥ AC.

Lời giải:

a) Chứng minh tứ giác AEFD nội tiếp:

Xét tứ giác AEFD:Góc AFD = 90° (vì AD là đường cao)

Góc AED = 90° (vì BE là đường cao)

Suy ra, góc AFD + góc AED = 180°

Vậy, tứ giác AEFD nội tiếp đường tròn (tổng hai góc đối bằng 180°).

b) Chứng minh ΔABD ~ ΔAKC và DF ⊥ AC:

Chứng minh ΔABD ~ ΔAKC:Xét ΔABD và ΔAKC:Góc ADB = góc AKC = 90° (vì AD, AK là đường cao)

Góc ABD = góc ACK (cùng chắn cung AC)

Do đó, ΔABD ~ ΔAKC (g-g).

Chứng minh DF ⊥ AC:Vì ΔABD ~ ΔAKC nên AB/AK = AD/AC.

Vì tứ giác AEFD nội tiếp nên góc FAD = góc FED.

Xét ΔAFD và ΔAKC:Góc AFD = góc AKC = 90°

Góc FAD = góc KAC

Do đó, ΔAFD ~ ΔAKC (g-g).

Suy ra, AF/AK = AD/AC.

Từ AB/AK = AD/AC và AF/AK = AD/AC, ta có: AB/AK = AF/AK => AB = AF.

Xét ΔABF và ΔADF:AB = AF

Góc BAF = góc DAF

AF là cạnh chung

Do đó, ΔABF = ΔADF (c-g-c).

Suy ra, góc AFB = góc AFD = 90°.

Vậy, DF ⊥ AC.dinhnhanhl