Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
giải theo chương trình lớp 9

 0
0
Trả lời câu hỏi của kim ngọc
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.
CÂU TRẢ LỜI



Timi
3 giờ trước
Trợ lý học tập AI - Câu trả lời này chỉ mang tính tham khảo
Câu 31:
Để giải bài toán này, chúng ta sẽ sử dụng một số kiến thức về hình học, đặc biệt là định lý về đường kính và dây cung trong đường tròn.
a) Tính độ dài đoạn thẳng CD khi \( R = 10 \, \text{cm} \) và \( OM = 6 \, \text{cm} \).
1. Xác định các yếu tố liên quan:
- \( O \) là tâm của đường tròn.
- \( R = 10 \, \text{cm} \) là bán kính của đường tròn.
- \( OM = 6 \, \text{cm} \) là khoảng cách từ tâm \( O \) đến đường thẳng \( d \).
2. Sử dụng định lý về đường kính và dây cung:
- Theo định lý, nếu \( OM \bot d \) thì \( M \) là trung điểm của dây cung \( CD \).
- Ta có \( OH^2 = R^2 - OM^2 \).
3. Tính \( OH \):
\[
OH = \sqrt{R^2 - OM^2} = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8 \, \text{cm}
\]
4. Tính độ dài đoạn thẳng \( CD \):
- Vì \( M \) là trung điểm của \( CD \), ta có:
\[
CD = 2 \times MH = 2 \times \sqrt{R^2 - OM^2} = 2 \times 8 = 16 \, \text{cm}
\]
b) Tìm bán kính của đường tròn biết \( CD = 24 \, \text{cm} \) và \( MH = 6 \, \text{cm} \).
1. Xác định các yếu tố liên quan:
- \( CD = 24 \, \text{cm} \)
- \( MH = 6 \, \text{cm} \)
2. Sử dụng định lý về đường kính và dây cung:
- Vì \( M \) là trung điểm của \( CD \), ta có:
\[
MH = \frac{CD}{2} = \frac{24}{2} = 12 \, \text{cm}
\]
3. Tính bán kính \( R \):
- Sử dụng công thức:
\[
MH = \sqrt{R^2 - OM^2}
\]
- Thay \( MH = 6 \, \text{cm} \) vào công thức:
\[
6 = \sqrt{R^2 - OM^2}
\]
- Giải phương trình:
\[
R^2 - OM^2 = 36
\]
- Vì \( OM = \frac{CD}{2} = 12 \, \text{cm} \), ta có:
\[
R^2 - 12^2 = 36
\]
\[
R^2 = 36 + 144 = 180
\]
\[
R = \sqrt{180} = 6\sqrt{5} \, \text{cm}
\]
Vậy bán kính của đường tròn là \( 6\sqrt{5} \, \text{cm} \).
Hãy giúp mọi người biết câu trả lời này thế nào?
0/5 (0 đánh giá)
 0
0
0 bình luận
Bình luận
_Bờ vai ank đấy tựa vào đi_
3 giờ trước
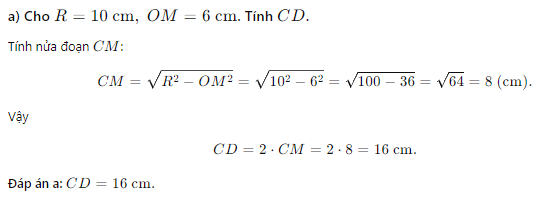
Hãy giúp mọi người biết câu trả lời này thế nào?
0/5 (0 đánh giá)
 0
0
0 bình luận
Bình luận
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
Nguyễn Phạm Khánh Linh
2 giờ trước
Bùi Ngọc Diễm
6 giờ trước
Top thành viên trả lời
Chọn thời gian
Mì 2 Tôm 5.220 Điểm
Brother 5.220 Điểm
Trịnh Minh Hoàng 4.860 Điểm
𝄞⨾𓍢ִ໋qυỳnн-anнн𝄞 3.740 Điểm
Ninh Hoàng 3.120 Điểm
FQA.vn Nền tảng kết nối cộng đồng hỗ trợ giải bài tập học sinh trong khối K12. Sản phẩm được phát triển bởi CÔNG TY TNHH CÔNG NGHỆ GIA ĐÌNH (FTECH CO., LTD)
Điện thoại: 1900636019
Email: info@fqa.vn
 Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Ô Chợ Dừa, Quận Đống Đa, Thành phố Hà Nội, Việt Nam.
Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Ô Chợ Dừa, Quận Đống Đa, Thành phố Hà Nội, Việt Nam.
Người chịu trách nhiệm quản lý nội dung: Nguyễn Tuấn Quang
Giấy phép thiết lập MXH số 07/GP-BTTTT do Bộ Thông tin và Truyền thông cấp ngày 05/01/2024
Copyright © 2023 fqa.vn All Rights Reserved



