Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
02/11/2023
Cho hình chóp S ABCD, đáy là tứ giác lồi ABCD có các cạnh đối không song song với nhau. Tìm giao tuyến của (SAC) và (SBD)

-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



02/11/2023
 0
0
02/11/2023
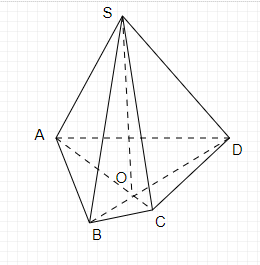
Trong mp (ABCD)
Kẻ AC cắt BD tại O
$\displaystyle \begin{array}{{>{\displaystyle}l}}
S\in ( SAC) ;S\in ( SBD)\\
O\in AC\in ( SAC) ;O\in BD\in ( SBD)\\
\Rightarrow SO=( SAC) \cap ( SBD)
\end{array}$
 0
0
02/11/2023
Xét 2 mp (SAC) và (SBD) ta có S là điểm chung thứ nhất (1)
Trong mp (abcd) gọi O là giao điểm của AC và BD
O∈AC ⊂(SAC)
{ ⇔O là điểm chung của (SAC) và SBD) (2)
O∈BD ⊂(SBD)
từ (1) và (2) suy ra giao tuyến của (SAC) và (SBD) là SO

 0
0
02/11/2023
Giao tuyến của hai mặt phẳng (SAC) và (SBD) là đường thẳng đi qua giao điểm của hai đường thẳng AC và BD.
Vì đáy ABCD là tứ giác lồi có các cạnh đối không song song với nhau, nên ta có:
AC || BD
Do đó, đường thẳng đi qua giao điểm của AC và BD sẽ song song với các cạnh của đáy ABCD.
Vậy, giao tuyến của (SAC) và (SBD) là đường thẳng song song với các cạnh của đáy ABCD.
 0
0
Nguyễn Thanhh Hoa
02/11/2023
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
2 giờ trước
2 giờ trước
2 giờ trước
3 giờ trước
3 giờ trước
Top thành viên trả lời







