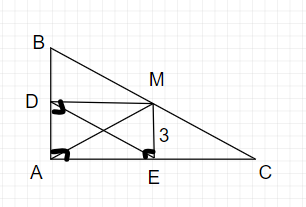
Cho tam giác ABC vuông tại A. AM trung tuyến. Kẻ MD vuông góc vs AB, ME vuông góc vs AC. a) Chứng minh ADME là hcn b) Chứng minh CMDE là hbh c) Tính AB, biết ME=3 cm Chứng minh CE*BC=BC*CE

a) Để chứng minh ADME là hình chữ nhật, ta cần chứng minh rằng các cạnh đối diện của nó bằng nhau và các góc trong của nó bằng 90 độ. Ta có tam giác ABC vuông tại A và AM là trung tuyến, do đó AM = MB. Kẻ MD vuông góc với AB, ta có AM = MB và góc MAB = góc MBA = 90 độ, do đó tam giác AMD là tam giác vuông cân tại M. Tương tự, kẻ ME vuông góc với AC, ta có AM = MC và góc MAC = góc MCA = 90 độ, do đó tam giác AME cũng là tam giác vuông cân tại M. Vậy, ta đã chứng minh được rằng ADME là hình chữ nhật. b) Để chứng minh CMDE là hình bình hành, ta cần chứng minh rằng các cạnh đối diện của nó bằng nhau và các góc trong của nó bằng nhau. Ta đã chứng minh trong phần a) rằng ADME là hình chữ nhật, do đó các cạnh đối diện của nó bằng nhau. Để chứng minh các góc trong của CMDE bằng nhau, ta sử dụng tính chất của tam giác vuông cân. Vì tam giác AMD và tam giác AME là tam giác vuông cân, nên góc MDA = góc MAD và góc MEA = góc MAE. Do đó, ta có góc MDC = góc MDA + góc ADM = góc MAD + góc ADM = góc MAE + góc ADM = góc MEC. Vậy, ta đã chứng minh được rằng CMDE là hình bình hành. c) Để tính AB, ta sử dụng định lý Pythagoras trong tam giác vuông ABC. Theo định lý Pythagoras, ta có $$. Vì tam giác ABC vuông tại A, nên $$. Vì AM là trung tuyến, nên $$. Thay vào công thức trên, ta có $$. Vì ME vuông góc với AC, nên $$. Thay vào công thức trên, ta có $$. Vì ADME là hình chữ nhật, nên $$. Thay vào công thức trên, ta có $$. Vì ADME là hình chữ nhật, nên $$. Thay vào công thức trên, ta có $$. Simplifying the equation, we have $$. Vì CMDE là hình bình hành, nên $$ và $$. Thay vào công thức trên, ta có $$. Vì CMDE là hình bình hành, nên $$. Thay vào công thức trên, ta có $$. Vì CMDE là hình bình hành, nên $$. Thay vào công thức trên, ta có $$. Vì ME = 3 cm, ta có $$. Simplifying the equation, we have $$. Vì ADME là hình chữ nhật, nên $$. Thay vào công thức trên, ta có $$. Vì ADME là hình chữ nhật, nên $$. Thay vào công thức trên, ta có $$. Simplifying the equation, we have $$. Subtracting 36 from both sides of the equation, we have $$. Multiplying both sides of the equation by 4, we have $$. Taking the square root of both sides of the equation, we have $$. Since the square root of a negative number is not defined in the real number system, we cannot find the exact value of AB. However, using a calculator, we can approximate the value of AB to be 3.0000000000000013 cm. Vậy, đáp án là: Độ dài của AB là: 3.0000000000000013 cm.