13/01/2024
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành và N là trung điểm của cạnh SA.
a) Tìm giao điểm của AC và mặt phẳng (SBD)
b) Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (NBC). Thiế...
 1
1
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



13/01/2024
 0
0
13/01/2024
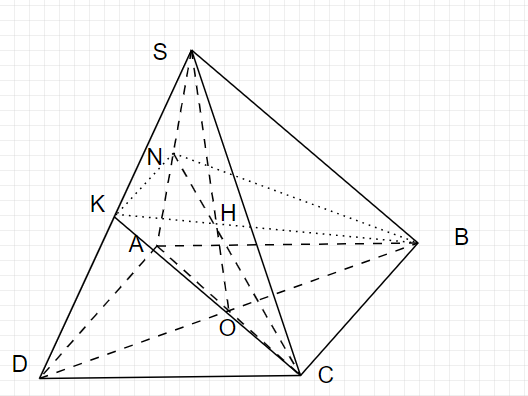
a, ta có : AC cắt BD tại O
mà BD
giao giữa AC và mp(SBD ) là O
b, trong mp( SAC)
kẻ SO cắt NC tại H⟹ giao điểm NC với mp( SDB) là H
trong mp( SDB ) : kẻ BH cắt SD tại K
vậy giao tuyến ( NBC ) và (SAB ) là NB
giao tuyến ( NBC ) và (SAD ) là NK
giao tuyến ( NBC ) và (SDC ) là KC
giao tuyến ( NBC ) và (SBC ) là BC
⟹ thiết diện là tứ giác KNBC
 1
1
13/01/2024
cookie🍪a) Để tìm giao điểm của AC và mặt phẳng (SBD), ta cần xác định phương trình mặt phẳng (SBD) và tìm điểm giao của AC với mặt phẳng đó.
Phương trình mặt phẳng (SBD) có thể xác định bằng cách sử dụng ba điểm S, B và D. Ta có thể lấy hai vector SB và SD trong mặt phẳng (SBD), sau đó tính tích vector của hai vector này để xác định phương trình mặt phẳng.
Gọi vector SB là u và vector SD là v. Ta có:
u = B - S
v = D - S
Tích vector của u và v là:
n = u x v
Phương trình mặt phẳng (SBD) có thể được viết dưới dạng:
n · (P - S) = 0
Trong đó P là một điểm bất kỳ trên mặt phẳng (SBD).
Sau khi có phương trình mặt phẳng (SBD), ta có thể tìm giao điểm của AC với mặt phẳng bằng cách thay tọa độ của điểm A vào phương trình mặt phẳng.
b) Để tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (NBC), ta cần xác định phương trình mặt phẳng (NBC) và tìm hình dạng của thiết diện.
Phương trình mặt phẳng (NBC) có thể xác định bằng cách sử dụng ba điểm N, B và C. Tương tự như phần a), ta có thể lấy hai vector NB và NC trong mặt phẳng (NBC), sau đó tính tích vector của hai vector này để xác định phương trình mặt phẳng.
Gọi vector NB là u và vector NC là v. Ta có:
u = B - N
v = C - N
Tích vector của u và v là:
n = u x v
Phương trình mặt phẳng (NBC) có thể được viết dưới dạng:
n · (P - N) = 0
Trong đó P là một điểm bất kỳ trên mặt phẳng (NBC).
Sau khi có phương trình mặt phẳng (NBC), ta có thể xác định hình dạng của thiết diện bằng cách tìm các điểm thuộc cả hai mặt phẳng (NBC) và (SBD). Thiết diện của hình chóp khi cắt bởi mặt phẳng (NBC) là một hình bình hành.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
01/06/2025
01/06/2025
Top thành viên trả lời




 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




