Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
Duy Nguyễn Khánh
03/10/2024
tìm tiệm cận, y' và vẽ bảng biến thiên

 1
1
Trả lời câu hỏi của Duy Nguyễn Khánh
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.
CÂU TRẢ LỜI



Timi
03/10/2024
Trợ lý học tập AI - Câu trả lời này chỉ mang tính tham khảo
Để tìm tiệm cận, đạo hàm \( y' \) và vẽ bảng biến thiên của hàm số, chúng ta sẽ thực hiện các bước sau:
Bước 1: Xác định miền xác định của hàm số
Giả sử hàm số đã cho là \( f(x) \). Chúng ta cần xác định miền xác định của hàm số này để đảm bảo rằng các phép tính sau đây đều hợp lý.
Bước 2: Tìm tiệm cận đứng
Tiệm cận đứng của hàm số \( f(x) \) là các đường thẳng \( x = a \) sao cho \( \lim_{x \to a^+} f(x) = \pm \infty \) hoặc \( \lim_{x \to a^-} f(x) = \pm \infty \).
Bước 3: Tìm tiệm cận ngang
Tiệm cận ngang của hàm số \( f(x) \) là các đường thẳng \( y = b \) sao cho \( \lim_{x \to \pm \infty} f(x) = b \).
Bước 4: Tính đạo hàm \( y' \)
Tính đạo hàm của hàm số \( f(x) \) để tìm các điểm cực trị và khoảng đồng biến, nghịch biến.
Bước 5: Xác định các điểm cực trị
Gọi \( f'(x) \) là đạo hàm của \( f(x) \). Các điểm cực trị xảy ra tại các điểm mà \( f'(x) = 0 \) hoặc \( f'(x) \) không tồn tại.
Bước 6: Vẽ bảng biến thiên
Dựa vào các thông tin trên, chúng ta sẽ vẽ bảng biến thiên của hàm số \( f(x) \).
Ví dụ cụ thể:
Giả sử hàm số đã cho là \( f(x) = \frac{x^2 - 1}{x - 1} \).
Bước 1: Xác định miền xác định
Miền xác định của hàm số là \( x \neq 1 \).
Bước 2: Tìm tiệm cận đứng
\( \lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} \frac{x^2 - 1}{x - 1} = \lim_{x \to 1^+} \frac{(x - 1)(x + 1)}{x - 1} = \lim_{x \to 1^+} (x + 1) = 2 \)
\( \lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} \frac{x^2 - 1}{x - 1} = \lim_{x \to 1^-} \frac{(x - 1)(x + 1)}{x - 1} = \lim_{x \to 1^-} (x + 1) = 2 \)
Vậy hàm số không có tiệm cận đứng.
Bước 3: Tìm tiệm cận ngang
\( \lim_{x \to \pm \infty} f(x) = \lim_{x \to \pm \infty} \frac{x^2 - 1}{x - 1} = \lim_{x \to \pm \infty} \frac{x^2(1 - \frac{1}{x^2})}{x(1 - \frac{1}{x})} = \lim_{x \to \pm \infty} \frac{x(1 - \frac{1}{x^2})}{1 - \frac{1}{x}} = \lim_{x \to \pm \infty} x = \pm \infty \)
Vậy hàm số không có tiệm cận ngang.
Bước 4: Tính đạo hàm \( y' \)
\( f(x) = \frac{x^2 - 1}{x - 1} = x + 1 \) (với \( x \neq 1 \))
\( f'(x) = 1 \)
Bước 5: Xác định các điểm cực trị
\( f'(x) = 1 \neq 0 \) nên hàm số không có điểm cực trị.
Bước 6: Vẽ bảng biến thiên
Bảng biến thiên của hàm số \( f(x) = x + 1 \) (với \( x \neq 1 \)):
| \( x \) | \( (-\infty, 1) \) | \( 1 \) | \( (1, \infty) \) |
|---------|---------------------|---------|--------------------|
| \( f(x) \) | \( x + 1 \) | Không xác định | \( x + 1 \) |
Hàm số \( f(x) = x + 1 \) (với \( x \neq 1 \)) là hàm số đồng biến trên cả miền xác định của nó.
Kết luận:
- Hàm số không có tiệm cận đứng và tiệm cận ngang.
- Đạo hàm của hàm số là \( f'(x) = 1 \).
- Hàm số đồng biến trên cả miền xác định của nó.
Câu 7.
Để khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = \frac{-x^2 + 1}{x}$, ta thực hiện các bước sau:
Bước 1: Xác định tập xác định
Hàm số $y = \frac{-x^2 + 1}{x}$ có mẫu số là $x$, do đó tập xác định của hàm số là:
\[ D = \mathbb{R} \setminus \{0\} \]
Bước 2: Tìm các giới hạn
- Giới hạn khi $x$ tiến đến vô cùng:
\[ \lim_{x \to \pm \infty} y = \lim_{x \to \pm \infty} \frac{-x^2 + 1}{x} = \lim_{x \to \pm \infty} \left( -x + \frac{1}{x} \right) = -\infty \]
- Giới hạn khi $x$ tiến đến 0 từ bên trái và bên phải:
\[ \lim_{x \to 0^-} y = \lim_{x \to 0^-} \frac{-x^2 + 1}{x} = -\infty \]
\[ \lim_{x \to 0^+} y = \lim_{x \to 0^+} \frac{-x^2 + 1}{x} = +\infty \]
Bước 3: Tìm các điểm đặc biệt
- Điểm cắt trục $Oy$: Đặt $x = 0$, nhưng $x = 0$ không thuộc tập xác định, nên hàm số không cắt trục $Oy$.
- Điểm cực trị: Để tìm điểm cực trị, ta tính đạo hàm của hàm số:
\[ y' = \frac{d}{dx} \left( \frac{-x^2 + 1}{x} \right) = \frac{(-2x)x - (-x^2 + 1)}{x^2} = \frac{-2x^2 + x^2 - 1}{x^2} = \frac{-x^2 - 1}{x^2} = -1 - \frac{1}{x^2} \]
Đặt $y' = 0$:
\[ -1 - \frac{1}{x^2} = 0 \Rightarrow \frac{1}{x^2} = -1 \]
Phương trình này vô nghiệm, do đó hàm số không có điểm cực trị.
Bước 4: Xét dấu của đạo hàm
\[ y' = -1 - \frac{1}{x^2} < 0 \quad \forall x \neq 0 \]
Do đó, hàm số nghịch biến trên cả hai khoảng $(-\infty, 0)$ và $(0, +\infty)$.
Bước 5: Vẽ đồ thị
- Đồ thị hàm số $y = \frac{-x^2 + 1}{x}$ có tiệm cận đứng là đường thẳng $x = 0$.
- Đồ thị không có tiệm cận ngang vì giới hạn khi $x$ tiến đến vô cùng là $-\infty$.
- Đồ thị không có điểm cực trị và luôn nghịch biến trên các khoảng $(-\infty, 0)$ và $(0, +\infty)$.
Kết luận
Hàm số $y = \frac{-x^2 + 1}{x}$ có tập xác định là $D = \mathbb{R} \setminus \{0\}$, không có điểm cực trị, luôn nghịch biến trên các khoảng $(-\infty, 0)$ và $(0, +\infty)$, và có tiệm cận đứng là đường thẳng $x = 0$.
Câu 8.
Để khảo sát và vẽ đồ thị của hàm số $y=\frac{x^2+2x-2}{x-1}$, ta thực hiện các bước sau:
1. Tìm tập xác định:
Hàm số xác định khi $x \neq 1$. Vậy tập xác định là $D = \mathbb{R} \setminus \{1\}$.
2. Tìm giao điểm với trục tọa độ:
- Giao điểm với trục $Oy$: Thay $x = 0$ vào hàm số:
\[
y = \frac{0^2 + 2 \cdot 0 - 2}{0 - 1} = \frac{-2}{-1} = 2
\]
Vậy giao điểm với trục $Oy$ là $(0, 2)$.
- Giao điểm với trục $Ox$: Thay $y = 0$ vào hàm số:
\[
0 = \frac{x^2 + 2x - 2}{x - 1}
\]
Điều này xảy ra khi $x^2 + 2x - 2 = 0$. Giải phương trình này:
\[
x = \frac{-2 \pm \sqrt{4 + 8}}{2} = \frac{-2 \pm \sqrt{12}}{2} = \frac{-2 \pm 2\sqrt{3}}{2} = -1 \pm \sqrt{3}
\]
Vậy giao điểm với trục $Ox$ là $(-1 + \sqrt{3}, 0)$ và $(-1 - \sqrt{3}, 0)$.
3. Tìm tiệm cận đứng và ngang:
- Tiệm cận đứng: Khi $x \to 1$, mẫu số $x - 1 \to 0$, nên hàm số có tiệm cận đứng là $x = 1$.
- Tiệm cận ngang: Ta xét giới hạn khi $x \to \infty$:
\[
y = \frac{x^2 + 2x - 2}{x - 1} = \frac{x^2(1 + \frac{2}{x} - \frac{2}{x^2})}{x(1 - \frac{1}{x})} = \frac{x(1 + \frac{2}{x} - \frac{2}{x^2})}{1 - \frac{1}{x}}
\]
Khi $x \to \infty$, $\frac{2}{x} \to 0$, $\frac{2}{x^2} \to 0$, $\frac{1}{x} \to 0$, nên:
\[
y \to x
\]
Vậy hàm số có tiệm cận ngang là $y = x$.
4. Tìm đạo hàm và cực trị:
- Đạo hàm của hàm số:
\[
y' = \left(\frac{x^2 + 2x - 2}{x - 1}\right)' = \frac{(2x + 2)(x - 1) - (x^2 + 2x - 2)}{(x - 1)^2} = \frac{2x^2 - 2x + 2x - 2 - x^2 - 2x + 2}{(x - 1)^2} = \frac{x^2 - 2x}{(x - 1)^2} = \frac{x(x - 2)}{(x - 1)^2}
\]
- Xét dấu đạo hàm:
\[
y' = 0 \Rightarrow x(x - 2) = 0 \Rightarrow x = 0 \text{ hoặc } x = 2
\]
Ta có bảng xét dấu:
\[
\begin{array}{c|ccc}
x & (-\infty, 0) & (0, 1) & (1, 2) & (2, \infty) \\
\hline
y' & + & - & - & + \\
\end{array}
\]
Từ bảng xét dấu, ta thấy:
- Hàm số đồng biến trên khoảng $(-\infty, 0)$ và $(2, \infty)$.
- Hàm số nghịch biến trên khoảng $(0, 1)$ và $(1, 2)$.
- Cực đại tại $x = 0$, $y = 2$.
- Cực tiểu tại $x = 2$, $y = 4$.
5. Vẽ đồ thị:
- Vẽ các giao điểm $(0, 2)$, $(-1 + \sqrt{3}, 0)$, $(-1 - \sqrt{3}, 0)$.
- Vẽ tiệm cận đứng $x = 1$ và tiệm cận ngang $y = x$.
- Vẽ các đoạn đồ thị theo tính chất đồng biến và nghịch biến đã tìm được.
- Đánh dấu các điểm cực đại $(0, 2)$ và cực tiểu $(2, 4)$.
Đồ thị của hàm số $y = \frac{x^2 + 2x - 2}{x - 1}$ sẽ có dạng như sau:
\[
\begin{tikzpicture}[scale=0.8]
\draw[->] (-5,0) -- (5,0) node[right] {$x$};
\draw[->] (0,-5) -- (0,5) node[above] {$y$};
\draw[dashed] (1,-5) -- (1,5);
\draw[dashed] (-5,-5) -- (5,5);
\draw[thick, smooth, domain=-4:0.9] plot (\x, {(\x\x + 2\x - 2)/(\x - 1)});
\draw[thick, smooth, domain=1.1:4] plot (\x, {(\x\x + 2\x - 2)/(\x - 1)});
\fill (0,2) circle (2pt) node[anchor=south east] {$(0, 2)$};
\fill (2,4) circle (2pt) node[anchor=south west] {$(2, 4)$};
\fill (-1 + sqrt(3),0) circle (2pt) node[anchor=north] {$(-1 + \sqrt{3}, 0)$};
\fill (-1 - sqrt(3),0) circle (2pt) node[anchor=north] {$(-1 - \sqrt{3}, 0)$};
\end{tikzpicture}
\]
Đây là đồ thị của hàm số $y = \frac{x^2 + 2x - 2}{x - 1}$.
Câu 9.
Để khảo sát và vẽ đồ thị của hàm số $y=\frac{-x^2-3x+4}{x+2}$, ta thực hiện các bước sau:
Bước 1: Xác định tập xác định
Tập xác định của hàm số là $D = \mathbb{R} \setminus \{-2\}$ vì mẫu số $x + 2$ phải khác 0.
Bước 2: Tìm giao điểm với trục tọa độ
- Giao điểm với trục Oy: Thay $x = 0$ vào hàm số:
\[ y = \frac{-0^2 - 3 \cdot 0 + 4}{0 + 2} = \frac{4}{2} = 2 \]
Giao điểm là $(0, 2)$.
- Giao điểm với trục Ox: Thay $y = 0$ vào hàm số:
\[ 0 = \frac{-x^2 - 3x + 4}{x + 2} \Rightarrow -x^2 - 3x + 4 = 0 \]
Giải phương trình bậc hai:
\[ x^2 + 3x - 4 = 0 \]
\[ (x + 4)(x - 1) = 0 \]
\[ x = -4 \text{ hoặc } x = 1 \]
Giao điểm là $(-4, 0)$ và $(1, 0)$.
Bước 3: Tìm tiệm cận
- Tiệm cận đứng: Khi $x \to -2$, mẫu số $x + 2 \to 0$. Ta có:
\[ \lim_{x \to -2^-} y = \lim_{x \to -2^-} \frac{-x^2 - 3x + 4}{x + 2} = +\infty \]
\[ \lim_{x \to -2^+} y = \lim_{x \to -2^+} \frac{-x^2 - 3x + 4}{x + 2} = -\infty \]
Tiệm cận đứng là đường thẳng $x = -2$.
- Tiệm cận斜渐近线:
\[ y = \frac{-x^2 - 3x + 4}{x + 2} = \frac{-(x^2 + 2x) - x + 4}{x + 2} = \frac{-(x^2 + 2x) - (x + 2) + 6}{x + 2} = -x - 1 + \frac{6}{x + 2} \]
当 \( x \to \pm \infty \) 时,\( \frac{6}{x + 2} \to 0 \),因此斜渐近线为 \( y = -x - 1 \)。
步骤 4:求导数并确定单调性
\[ y' = \left( \frac{-x^2 - 3x + 4}{x + 2} \right)' = \frac{(-2x - 3)(x + 2) - (-x^2 - 3x + 4)}{(x + 2)^2} = \frac{-2x^2 - 7x - 6 + x^2 + 3x - 4}{(x + 2)^2} = \frac{-x^2 - 4x - 10}{(x + 2)^2} \]
令 \( y' = 0 \):
\[ -x^2 - 4x - 10 = 0 \]
\[ x^2 + 4x + 10 = 0 \]
判别式 \( \Delta = 16 - 40 = -24 < 0 \),因此没有实根。这意味着导数始终为负,函数在定义域内单调递减。
步骤 5:绘制图形
根据以上分析,我们可以绘制函数的图形。函数在 \( x = -2 \) 处有垂直渐近线,在 \( x \to \pm \infty \) 时有斜渐近线 \( y = -x - 1 \)。函数在 \( x = 0 \) 时与 \( y \) 轴相交于点 \( (0, 2) \),在 \( x = -4 \) 和 \( x = 1 \) 时与 \( x \) 轴相交于点 \( (-4, 0) \) 和 \( (1, 0) \)。函数在整个定义域内单调递减。
最终答案是:
- 集合定义:\( D = \mathbb{R} \setminus \{-2\} \)
- 与 \( y \) 轴的交点:\( (0, 2) \)
- 与 \( x \) 轴的交点:\( (-4, 0) \) 和 \( (1, 0) \)
- 垂直渐近线:\( x = -2 \)
- 斜渐近线:\( y = -x - 1 \)
- 函数在定义域内单调递减
图形如下所示(请参考绘图工具或软件进行绘制)。
结论:
通过以上步骤,我们已经完成了对函数 \( y = \frac{-x^2 - 3x + 4}{x + 2} \) 的详细分析和图形绘制。
Câu 10.
Để khảo sát sự biến thiên và vẽ đồ thị của hàm số $y=f(x)=\frac{x^2+4x+5}{x+2}$, ta thực hiện các bước sau:
Bước 1: Tìm tập xác định
Tập xác định của hàm số là $D=\mathbb{R}\setminus \{-2\}$ vì mẫu số $x+2$ phải khác 0.
Bước 2: Tìm giới hạn
- $\lim_{x \to -2^-} f(x) = +\infty$
- $\lim_{x \to -2^+} f(x) = -\infty$
- $\lim_{x \to \pm \infty} f(x) = x$
Do đó, đường thẳng $x = -2$ là đường tiệm cận đứng và đường thẳng $y = x$ là đường tiệm cận xiên.
Bước 3: Tìm đạo hàm
$f'(x) = \frac{(2x+4)(x+2)-(x^2+4x+5)}{(x+2)^2} = \frac{x^2+4x+8-x^2-4x-5}{(x+2)^2} = \frac{3}{(x+2)^2}$
Bước 4: Xác định dấu của đạo hàm
$f'(x) > 0$ với mọi $x \neq -2$. Do đó, hàm số đồng biến trên khoảng $(-\infty, -2)$ và $(-2, +\infty)$.
Bước 5: Tìm cực trị
Hàm số không có cực trị vì đạo hàm không đổi dấu.
Bước 6: Tìm điểm đặc biệt
- Điểm giao với trục Oy: $f(0) = \frac{5}{2}$. Vậy điểm $(0, \frac{5}{2})$ nằm trên đồ thị.
- Điểm giao với trục Ox: $f(x) = 0$ không có nghiệm, vậy đồ thị không cắt trục Ox.
Bước 7: Vẽ đồ thị
- Đồ thị đi qua điểm $(0, \frac{5}{2})$.
- Đồ thị có tiệm cận đứng là $x = -2$ và tiệm cận xiên là $y = x$.
- Đồ thị đồng biến trên cả hai khoảng $(-\infty, -2)$ và $(-2, +\infty)$.
Đồ thị của hàm số $y = \frac{x^2+4x+5}{x+2}$:
[Đồ thị sẽ được vẽ dựa trên các thông tin đã tìm ra ở trên]
Kết luận: Đồ thị của hàm số $y = \frac{x^2+4x+5}{x+2}$ là một đồ thị đồng biến trên cả hai khoảng $(-\infty, -2)$ và $(-2, +\infty)$, có tiệm cận đứng là $x = -2$ và tiệm cận xiên là $y = x$, đi qua điểm $(0, \frac{5}{2})$.
Câu 11.
Để khảo sát sự biến thiên và vẽ đồ thị của hàm số $y=f(x)=\frac{-x^2-x+2}{x+1}$, ta thực hiện các bước sau:
Bước 1: Xác định tập xác định
Tập xác định của hàm số là $D=\mathbb{R}\setminus \left\{-1\right\}$ vì mẫu số $x+1$ không được phép bằng 0.
Bước 2: Tìm giao điểm với trục tọa độ
- Giao điểm với trục Oy: Thay $x=0$ vào hàm số, ta có $y=\frac{-0^2-0+2}{0+1}=2$. Vậy giao điểm là $(0, 2)$.
- Giao điểm với trục Ox: Thay $y=0$ vào hàm số, ta có $\frac{-x^2-x+2}{x+1}=0$. Điều này xảy ra khi $-x^2-x+2=0$, tức là $x^2+x-2=0$. Giải phương trình bậc hai này, ta tìm được $x_1=1$ và $x_2=-2$. Vậy giao điểm là $(1, 0)$ và $(-2, 0)$.
Bước 3: Xét tính chẵn lẻ
$f(-x)=\frac{-(-x)^2-(-x)+2}{-x+1}=\frac{-x^2+x+2}{-x+1}$. Ta thấy rằng $f(-x)\neq f(x)$ và $f(-x)\neq -f(x)$, do đó hàm số không chẵn cũng không lẻ.
Bước 4: Tìm giới hạn
- Giới hạn tại vô cực: $\lim_{x\to \pm \infty }f(x)=\lim_{x\to \pm \infty }\frac{-x^2-x+2}{x+1}=\lim_{x\to \pm \infty }\frac{-x^2(1+\frac{1}{x}-\frac{2}{x^2})}{x(1+\frac{1}{x})}=-x=-\infty$.
- Giới hạn tại $x=-1$: $\lim_{x\to -1^-}f(x)=+\infty$ và $\lim_{x\to -1^+}f(x)=-\infty$. Do đó, đường thẳng $x=-1$ là đường tiệm cận đứng.
Bước 5: Tìm đạo hàm và các điểm đặc biệt
$f'(x)=\frac{d}{dx}\left(\frac{-x^2-x+2}{x+1}\right)=\frac{(-2x-1)(x+1)-(-x^2-x+2)}{(x+1)^2}=\frac{-x^2-2x-1+x^2+x-2}{(x+1)^2}=\frac{-x-3}{(x+1)^2}$.
Đạo hàm bằng 0 khi $-x-3=0$, tức là $x=-3$. Ta có $f(-3)=\frac{-(-3)^2-(-3)+2}{-3+1}=\frac{-9+3+2}{-2}=\frac{-4}{-2}=2$. Vậy điểm đặc biệt là $(-3, 2)$.
Bước 6: Xét dấu đạo hàm và vẽ đồ thị
- Khi $x< -3$, $f'(x)< 0$ nên hàm số giảm.
- Khi $-3< x< -1$, $f'(x)>0$ nên hàm số tăng.
- Khi $x>-1$, $f'(x)< 0$ nên hàm số giảm.
Bước 7: Vẽ đồ thị
- Đồ thị đi qua các điểm $(0, 2)$, $(1, 0)$, $(-2, 0)$, $(-3, 2)$.
- Đồ thị có đường tiệm cận đứng là $x=-1$.
- Đồ thị giảm từ trái sang phải ngoại trừ đoạn từ $x=-3$ đến $x=-1$ là tăng.
Vậy đồ thị của hàm số $y=f(x)=\frac{-x^2-x+2}{x+1}$ đã được khảo sát và vẽ đầy đủ.
Hãy giúp mọi người biết câu trả lời này thế nào?
1.0/5 (1 đánh giá)
 0
0
0 bình luận
Bình luận
Ha
03/10/2024
Câu 7:
$\displaystyle \begin{array}{{>{\displaystyle}l}}
y=\frac{-x^{2} +1}{x} =-x+\frac{1}{x}\\
y'=-1-\frac{1}{x^{2}} =-\left( 1+\frac{1}{x^{2}}\right) < 0\\
\lim _{x\rightarrow -\infty } y=+\infty \\
\lim _{x\rightarrow +\infty } y=-\infty \\
\lim _{x\rightarrow 0^{+}} y=+\infty \\
\lim _{x\rightarrow 0^{-}} y=-\infty \\
BBT:
\end{array}$
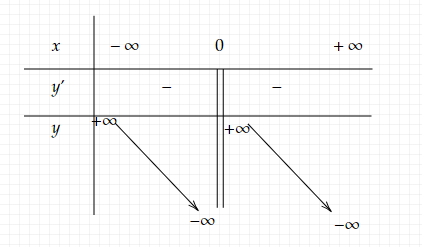
Hãy giúp mọi người biết câu trả lời này thế nào?
0/5 (0 đánh giá)
 0
0
0 bình luận
Bình luận
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
thekingchau
31/08/2025
thekingchau
31/08/2025
thekingchau
31/08/2025
thekingchau
31/08/2025
Top thành viên trả lời
Chọn thời gian
lười 210 Điểm
Haciicuti 70 Điểm
tú nguyen 50 Điểm
⋆.˚✮🎧✮˚.⋆ɱɑɨ 40 Điểm
sunnyy 30 Điểm


FQA.vn Nền tảng kết nối cộng đồng hỗ trợ giải bài tập học sinh trong khối K12. Sản phẩm được phát triển bởi CÔNG TY TNHH CÔNG NGHỆ GIA ĐÌNH (FTECH CO., LTD)
Điện thoại: 1900636019
Email: info@fqa.vn
 Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Ô Chợ Dừa, Quận Đống Đa, Thành phố Hà Nội, Việt Nam.
Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Ô Chợ Dừa, Quận Đống Đa, Thành phố Hà Nội, Việt Nam.
Người chịu trách nhiệm quản lý nội dung: Nguyễn Tuấn Quang
Giấy phép thiết lập MXH số 07/GP-BTTTT do Bộ Thông tin và Truyền thông cấp ngày 05/01/2024
Copyright © 2023 fqa.vn All Rights Reserved





