Tất cả
Hỏi bài tập Toán Học
Vật Lý
Hóa Học
Tiếng Anh
Ngữ Văn
Hỏi đời sống Tâm lý cảm xúc
Tình cảm
Gia đình bạn bè
Cơ thể & Dậy thì
Giải trí
Mạng xã hội
Định hướng cuộc sống
Hỏi đáp ẩn danh
29/10/2024
Câu 4. CChi phí tiền xăng C C(v) = 16000/v + 5/2 * v (đồng) phụ thuộc tốc độ trung bình (0 < v <= 120) . Vận hành để tiết kiệm tiền xăng nhất? v(km / h) theo công thức: xe với tốc độ trung bình v(km /...
 0
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



29/10/2024
 0
0
29/10/2024
Xét hàm số
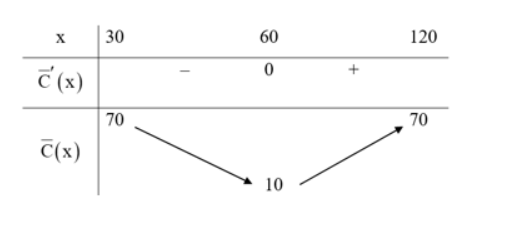
1. Tập xác định: D = [30; 120].
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm
Trên khoảng (30; 60),
Trên khoảng (60; 120)
● Cực trị:
Hàm số có một điểm cực trị là điểm cực tiểu tại x = 60 và
Bảng biến thiên:
Đồ thị:
Đồ thị hàm số không cắt các trục tọa độ.
Điểm cực tiểu của đồ thị hàm số là (60; 10).
Đồ thị hàm số đi qua các điểm (30; 70), (40; 30), (80; 20), (90; 30) và (120; 70).
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.
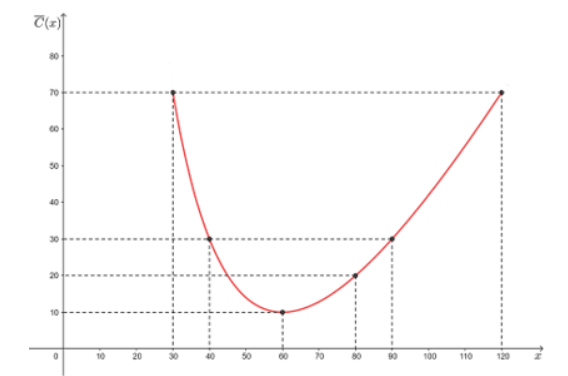
ta thấy trên đoạn [30; 120], giá trị nhỏ nhất của hàm số
Vậy số phần ăn là 60 thì chi phí trung bình của một phần ăn là thấp nhất.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
5 giờ trước
6 giờ trước
6 giờ trước
6 giờ trước
6 giờ trước
Top thành viên trả lời








