giúp em vứi mn

a) Sắp xếp lại mẫu số liệu trên theo thứ tự không giảm, ta được:

147              187,1           200,7           242,2           251,4           258,4           288,5

298,1           305              332              341,4           388,6           400              413,5

413,5           421              432,2           475              520              522,9

Khoảng biến thiên của mẫu số liệu trên là:

R = 522,9 – 147 = 375,9 (mm).

Cỡ mẫu n = 20.

Tứ phân vị thứ nhất là trung vị của mẫu số liệu:

147; 187,1; 200,7; 242,2; 251,4; 258,4 ; 288,5; 298,1; 305 ; 332.

Do đó,$$
Tứ phân vị thứ ba là trung vị của mẫu số liệu:

341,4; 388,6 ; 400; 413,5; 413,5 ; 421; 432,2; 475; 520; 522,9.

Do đó,$$
Khoảng tứ phân vị của mẫu số liệu đã cho là:

∆Q = Q3 – Q1 = 417,25 – 254,9 = 162,35.

b) Nhóm đầu tiên là [140; 240), ta chọn 3 nhóm còn lại là

[240; 340), [340; 440), [440; 540).

Từ bảng thống kê ban đầu, ta lập được bảng tần số ghép nhóm như sau:

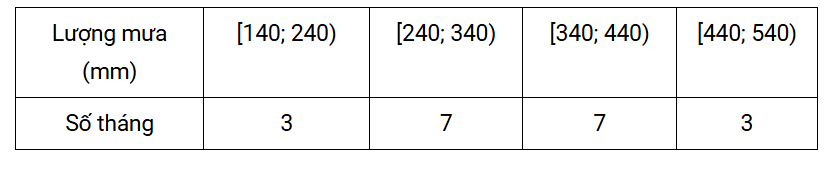
c) Cỡ mẫu n = 20.

Khoảng biến thiên của mẫu số liệu ghép nhóm là

R' = 540 – 140 = 400 (mm).

Gọi x1; x2; …; x20 là mẫu số liệu gốc về lượng mưa đo được vào tháng 7 từ năm 2002 đến 2021 tại một trạm quan trắc đặt ở Cà Mau được xếp theo thứ tự không giảm.

Ta có x1; x2; x3 ∈ [140; 240), x4; …; x10 ∈ [240; 340),

         x11; …; x17 ∈ [340; 440), x18; x19; x20 ∈ [440; 540).

Tứ phân vị thứ nhất của mẫu số liệu gốc là  ∈ [240; 340).

Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: .

Tứ phân vị thứ ba của mẫu số liệu gốc là $$∈ [340; 440).

Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
$$
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
$$≈ 142,86.

Ta thấy khoảng biến thiên của mẫu số liệu ghép nhóm lớn hơn mẫu số liệu đã cho; khoảng tứ phân vị của mẫu số liệu ghép nhóm nhỏ hơn mẫu số liệu đã cho.