Câu 4: Một bể chứa nhiên liệu hình trụ đặt nằm ngang, có chiều dài 5 m, có bán kính đáy 1m. Chiều cao của mực nhiên liệu là 1,5m. Tính thể tích phần nhiên liệu trong bể (theo đơn vị m', làm tròn đến ch...

Thể tích của cả bể nhiên liệu là: $\displaystyle V=\pi r^{2} .h=\pi .1^{2} .5=5\pi \left( m^{3}\right)$
Gọi $\displaystyle V_{1}$ là thể tích phần trống nhiên liệu, $\displaystyle V_{2}$ là phần thể tích chứa nhiên liệu.
Khi đó, $\displaystyle V_{2} =V-V_{1}$. Để tìm $\displaystyle V_{2}$ theo yêu cầu đề bài, ta tính $\displaystyle V_{1}$ trước.
$\displaystyle V_{1} =B_{trong} .h$ với $\displaystyle B_{trong}$ là phần diện tích đáy không chứa nhiên liệu.
Chọn hệ trục Oxy như hình vẽ:

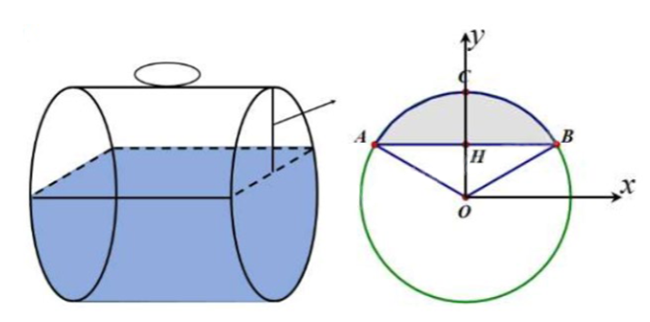
$\displaystyle B_{trong} =S_{ACB} =2S_{BHC}$
chiều cao mực nhiên liệu là 1,5m, bán kính đáy bằng 1m nên OH=0,5m
Ta có: $\displaystyle HB=\sqrt{OB^{2} -OH^{2}} =\sqrt{1^{2} -0,5^{2}} =\frac{\sqrt{3}}{2}$
Vậy $\displaystyle B\left(\frac{\sqrt{3}}{2} ;\frac{1}{2}\right)$
Đường tròn đáy là đường tròn tâm O, bán kính R=1 nên có phương trình $\displaystyle x^{2} +y^{2} =1$. Khi đó phần đồ thị nửa đường trong nằm trên trục hoành có phương trình $\displaystyle y=\sqrt{1-x^{2}}$
$\displaystyle S_{BHC}$ là phần diện tích giới hạn bởi nửa đường tròn $\displaystyle y=\sqrt{1-x^{2}}$, đường thẳng $\displaystyle y=\frac{1}{2}$, trục tung $\displaystyle x=0$ và điểm B có hoành độ $\displaystyle x=\frac{\sqrt{3}}{2}$
Ứng dụng tích phân để tính $\displaystyle S_{BHC}$, ta có:
$\displaystyle S_{BHC} =\int _{0}^{\frac{\sqrt{3}}{2}} |\sqrt{1-x^{2}} -\frac{1}{2} |dx=\int _{0}^{\frac{\sqrt{3}}{2}}\left(\sqrt{1-x^{2}} -\frac{1}{2}\right) dx\ $(do trong khoảng $\displaystyle \left( 0;\frac{\sqrt{3}}{2}\right)$ đồ thị $\displaystyle y=\sqrt{1-x^{2}}$ nằm phía trên đồ thị $\displaystyle y=\frac{1}{2}$, suy ra$\displaystyle \sqrt{1-x^{2}}  >\frac{1}{2} \Longrightarrow \sqrt{1-x^{2}} -\frac{1}{2}  >0\Longrightarrow |\sqrt{1-x^{2}} -\frac{1}{2} |=\sqrt{1-x^{2}} -\frac{1}{2})$
$\displaystyle S_{BHC} =\int _{0}^{\frac{\sqrt{3}}{2}}\left(\sqrt{1-x^{2}} -\frac{1}{2}\right) dx=\int _{0}^{\frac{\sqrt{3}}{2}}\left(\sqrt{1-x^{2}}\right) dx-\frac{1}{2}\int _{0}^{\frac{\sqrt{3}}{2}} dx$
Ta có: 
$\displaystyle \frac{1}{2}\int _{0}^{\frac{\sqrt{3}}{2}} dx=\frac{1}{2} .\left(\frac{\sqrt{3}}{2} -0\right) =\frac{\sqrt{3}}{4}$
Để tính $\displaystyle \int _{0}^{\frac{\sqrt{3}}{2}}\left(\sqrt{1-x^{2}}\right) dx$, ta đặt $\displaystyle x=\sin t\Longrightarrow dx=\cos tdt$
Đổi cận

Khi đó $\displaystyle \int _{0}^{\frac{\sqrt{3}}{2}}\left(\sqrt{1-x^{2}}\right) dx=\int _{0}^{\frac{\pi }{3}}\left(\sqrt{1-\sin^{2} t}\right)\cos tdt=\int _{0}^{\frac{\pi }{3}} |\cos t|\cos tdt=\int _{0}^{\frac{\pi }{3}}\cos^{2} tdt$ (vì trong khoảng $\displaystyle \left( 0;\frac{\pi }{3}\right)$ $\displaystyle \cos t >0\Longrightarrow |\cos t|=\cos t)$
$\displaystyle  \begin{array}{{>{\displaystyle}l}}
\Longrightarrow \int _{0}^{\frac{\sqrt{3}}{2}}(\sqrt{1-x^{2}} dx=\int _{0}^{\frac{\pi }{3}}\cos^{2} tdt=\int _{0}^{\frac{\pi }{3}}\frac{1+\cos 2x}{2} tdt=\int _{0}^{\frac{\pi }{3}}\left(\frac{1}{2} +\frac{\cos 2x}{2}\right) tdt\\
=\left(\frac{x}{2} +\frac{\sin 2x}{4}\right) |_{0}^{\frac{\pi }{3}} =\frac{\pi }{6} +\frac{\sin\frac{\pi }{3}}{4} =\frac{\pi }{6} +\frac{\sqrt{3}}{8}
\end{array}$
$\displaystyle S_{BHC} =\int _{0}^{\frac{\sqrt{3}}{2}}\left(\sqrt{1-x^{2}}\right) dx-\frac{1}{2}\int _{0}^{\frac{\sqrt{3}}{2}} dx=\frac{\pi }{6} +\frac{\sqrt{3}}{8} -\frac{\sqrt{3}}{4} =\frac{\pi }{6} -\frac{\sqrt{3}}{8}$
$\displaystyle  \begin{array}{{>{\displaystyle}l}}
B_{trong} =2S_{BHC} =2.\left(\frac{\pi }{6} -\frac{\sqrt{3}}{8}\right) =\frac{\pi }{3} -\frac{\sqrt{3}}{4}\\
V_{1} =B_{trong} .h=5.\left(\frac{\pi }{3} -\frac{\sqrt{3}}{4}\right)
\end{array}$
Thể tích phần nhiên liệu trong bể là: 
$\displaystyle V_{2} =V-V_{1} =5\pi -5.\left(\frac{\pi }{3} -\frac{\sqrt{3}}{4}\right) \approx 12,6\ \left( m^{3}\right)$