giúp em với ạ giải ngắn thyi ạ

Câu 17. Để tính giá trị biểu thức \( T = abc \), ta cần tìm các hệ số \( a \), \( b \), và \( c \) trong biểu thức \( F(x) = (ax^2 + bx + c) \sqrt{2x - 4} \). Trước tiên, ta tính đạo hàm của \( F(x) \): \[ F'(x) = \left( ax^2 + bx + c \right)' \sqrt{2x - 4} + \left( ax^2 + bx + c \right) \left( \sqrt{2x - 4} \right)' \] Ta có: \[ \left( ax^2 + bx + c \right)' = 2ax + b \] \[ \left( \sqrt{2x - 4} \right)' = \frac{1}{2} (2x - 4)^{-\frac{1}{2}} \cdot 2 = \frac{1}{\sqrt{2x - 4}} \] Do đó: \[ F'(x) = (2ax + b) \sqrt{2x - 4} + (ax^2 + bx + c) \frac{1}{\sqrt{2x - 4}} \] Nhân cả hai vế với \(\sqrt{2x - 4}\) để đơn giản hóa: \[ F'(x) \sqrt{2x - 4} = (2ax + b)(2x - 4) + (ax^2 + bx + c) \] Phân tích biểu thức: \[ F'(x) \sqrt{2x - 4} = 2ax(2x - 4) + b(2x - 4) + ax^2 + bx + c \] \[ = 4ax^2 - 8ax + 2bx - 4b + ax^2 + bx + c \] \[ = 5ax^2 + (-8a + 3b)x + (-4b + c) \] Theo đề bài, \( F'(x) = f(x) = \frac{10x^2 - 13x - 252}{\sqrt{2x - 4}} \). Do đó: \[ 5ax^2 + (-8a + 3b)x + (-4b + c) = 10x^2 - 13x - 252 \] So sánh hệ số tương ứng: 1. \( 5a = 10 \Rightarrow a = 2 \) 2. \( -8a + 3b = -13 \Rightarrow -8(2) + 3b = -13 \Rightarrow -16 + 3b = -13 \Rightarrow 3b = 3 \Rightarrow b = 1 \) 3. \( -4b + c = -252 \Rightarrow -4(1) + c = -252 \Rightarrow -4 + c = -252 \Rightarrow c = -248 \) Vậy \( a = 2 \), \( b = 1 \), và \( c = -248 \). Giá trị biểu thức \( T = abc \) là: \[ T = 2 \times 1 \times (-248) = -496 \] Đáp số: \( T = -496 \) Câu 18. Để tính giá trị của biểu thức \( T = a - b \), chúng ta cần thực hiện các bước sau: 1. Tìm giá trị của tích phân \(\int^5_{-1} x^2 |x-1| dx\): Ta chia đoạn tích phân thành hai phần dựa vào điểm \( x = 1 \): \[ \int^5_{-1} x^2 |x-1| dx = \int^1_{-1} x^2 (1-x) dx + \int^5_1 x^2 (x-1) dx \] 2. Tính từng phần tích phân: - Phần thứ nhất: \(\int^1_{-1} x^2 (1-x) dx\) \[ \int^1_{-1} x^2 (1-x) dx = \int^1_{-1} (x^2 - x^3) dx \] Tính từng phần riêng lẻ: \[ \int^1_{-1} x^2 dx = \left[ \frac{x^3}{3} \right]^1_{-1} = \frac{1^3}{3} - \frac{(-1)^3}{3} = \frac{1}{3} + \frac{1}{3} = \frac{2}{3} \] \[ \int^1_{-1} x^3 dx = \left[ \frac{x^4}{4} \right]^1_{-1} = \frac{1^4}{4} - \frac{(-1)^4}{4} = \frac{1}{4} - \frac{1}{4} = 0 \] Vậy: \[ \int^1_{-1} (x^2 - x^3) dx = \frac{2}{3} - 0 = \frac{2}{3} \] - Phần thứ hai: \(\int^5_1 x^2 (x-1) dx\) \[ \int^5_1 x^2 (x-1) dx = \int^5_1 (x^3 - x^2) dx \] Tính từng phần riêng lẻ: \[ \int^5_1 x^3 dx = \left[ \frac{x^4}{4} \right]^5_1 = \frac{5^4}{4} - \frac{1^4}{4} = \frac{625}{4} - \frac{1}{4} = \frac{624}{4} = 156 \] \[ \int^5_1 x^2 dx = \left[ \frac{x^3}{3} \right]^5_1 = \frac{5^3}{3} - \frac{1^3}{3} = \frac{125}{3} - \frac{1}{3} = \frac{124}{3} \] Vậy: \[ \int^5_1 (x^3 - x^2) dx = 156 - \frac{124}{3} = \frac{468}{3} - \frac{124}{3} = \frac{344}{3} \] 3. Tổng hợp kết quả: \[ \int^5_{-1} x^2 |x-1| dx = \frac{2}{3} + \frac{344}{3} = \frac{346}{3} \] 4. Phân số tối giản: \(\frac{346}{3}\) đã là phân số tối giản, vậy \(a = 346\) và \(b = 3\). 5. Tính giá trị của biểu thức \(T = a - b\): \[ T = 346 - 3 = 343 \] Đáp số: \(T = 343\). Câu 19. Ta có: $\int^c_af(x)dx=\int^b_af(x)dx+\int^c_bf(x)dx$ $=\left | \int^b_af(x)dx \right |-\left | \int^c_bf(x)dx \right |$ $=S_1-S_2$ $=294-327=-33$ Câu 20. Để tính diện tích phần gạch chéo trong hình vẽ, ta cần xác định diện tích giữa hai đồ thị từ điểm giao thứ nhất đến điểm giao thứ hai của chúng. Bước 1: Xác định các điểm giao của đồ thị $y=x^2$ và đường thẳng $y=mx+n$. - Ta có phương trình $x^2 = mx + n$. - Sắp xếp lại phương trình này thành dạng chuẩn: $x^2 - mx - n = 0$. Bước 2: Tìm nghiệm của phương trình bậc hai $x^2 - mx - n = 0$. - Áp dụng công thức nghiệm của phương trình bậc hai: $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, với $a = 1$, $b = -m$, và $c = -n$. - Do đó, $x = \frac{m \pm \sqrt{m^2 + 4n}}{2}$. Bước 3: Xác định giá trị của $m$ và $n$ dựa vào các điểm đã cho. - Điểm $(3, 9)$ nằm trên cả hai đồ thị, do đó thay vào phương trình $y = mx + n$: $9 = 3m + n$. - Ta cũng biết rằng điểm $(0, 0)$ nằm trên đồ thị $y = x^2$, do đó thay vào phương trình $y = mx + n$: $0 = m \cdot 0 + n \Rightarrow n = 0$. - Từ đó suy ra $9 = 3m \Rightarrow m = 3$. Bước 4: Xác định diện tích giữa hai đồ thị từ $x = 0$ đến $x = 3$. - Diện tích cần tính là $\int_{0}^{3} (x^2 - (3x)) \, dx$. - Tính tích phân: $\int_{0}^{3} (x^2 - 3x) \, dx = \left[ \frac{x^3}{3} - \frac{3x^2}{2} \right]_{0}^{3}$. - Thay cận: $\left( \frac{3^3}{3} - \frac{3 \cdot 3^2}{2} \right) - \left( \frac{0^3}{3} - \frac{3 \cdot 0^2}{2} \right) = \left( 9 - \frac{27}{2} \right) - 0 = 9 - 13.5 = -4.5$. Do diện tích không thể âm, ta lấy giá trị tuyệt đối: $|-4.5| = 4.5$. Vậy diện tích phần gạch chéo là $4.5$. Câu 21. Để giải bài toán này, chúng ta sẽ thực hiện các bước sau: 1. Xác định phương trình của parabol: - Ta chọn hệ tọa độ sao cho đỉnh của parabol trùng với gốc tọa độ (0,0) và trục đối xứng của parabol trùng với trục y. - Chiều cao từ mặt đất đến đỉnh là 2,25 mét, tức là điểm (0, 2,25). - Chiều rộng tiếp giáp với mặt đất là 3 mét, tức là hai điểm (-1,5, 0) và (1,5, 0). Phương trình của parabol có dạng: \[ y = ax^2 + bx + c \] Vì đỉnh của parabol là (0, 2,25), ta có: \[ y = ax^2 + 2,25 \] Thay điểm (1,5, 0) vào phương trình: \[ 0 = a(1,5)^2 + 2,25 \] \[ 0 = 2,25a + 2,25 \] \[ 2,25a = -2,25 \] \[ a = -1 \] Vậy phương trình của parabol là: \[ y = -x^2 + 2,25 \] 2. Tính diện tích của hình parabol: Diện tích của hình parabol có thể tính bằng cách tích phân phương trình của parabol từ -1,5 đến 1,5: \[ A = \int_{-1,5}^{1,5} (-x^2 + 2,25) \, dx \] Tính tích phân: \[ A = \left[ -\frac{x^3}{3} + 2,25x \right]_{-1,5}^{1,5} \] \[ A = \left( -\frac{(1,5)^3}{3} + 2,25(1,5) \right) - \left( -\frac{(-1,5)^3}{3} + 2,25(-1,5) \right) \] \[ A = \left( -\frac{3,375}{3} + 3,375 \right) - \left( \frac{3,375}{3} - 3,375 \right) \] \[ A = \left( -1,125 + 3,375 \right) - \left( 1,125 - 3,375 \right) \] \[ A = 2,25 - (-2,25) \] \[ A = 2,25 + 2,25 \] \[ A = 4,5 \text{ m}^2 \] 3. Tính số tiền nhà trường phải trả: Giá thuê mỗi mét vuông là 1,5 triệu đồng, vậy số tiền nhà trường phải trả là: \[ \text{Số tiền} = 4,5 \times 1,5 = 6,75 \text{ triệu đồng} \] Đáp số: 6,75 triệu đồng. 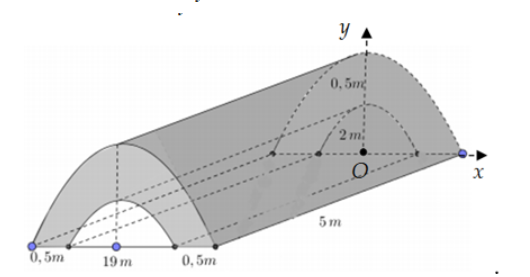Câu 22. Để tính số tiền mà tỉnh Phú Yên cần bỏ ra để xây cây cầu, ta cần tính thể tích của phần bê tông dùng để đổ cây cầu. Ta sẽ chia phần bê tông thành hai phần đối xứng qua trục Oy và tính thể tích của một phần rồi nhân đôi. Phần bê tông bên trái có dạng một khối bê tông giữa hai đường parabol y = -x^2 + 4 và y = -x^2 + 1 từ x = -2 đến x = 0. Thể tích của một phần này là: \[ V_1 = \int_{-2}^{0} \left[(-x^2 + 4) - (-x^2 + 1)\right] dx \] \[ V_1 = \int_{-2}^{0} (4 - 1) dx \] \[ V_1 = \int_{-2}^{0} 3 dx \] \[ V_1 = 3x \Big|_{-2}^{0} \] \[ V_1 = 3(0) - 3(-2) \] \[ V_1 = 6 \] Vậy thể tích của cả hai phần là: \[ V = 2 \times V_1 = 2 \times 6 = 12 \] Số tiền cần bỏ ra để xây cây cầu là: \[ Tiền = 12 \times 5 = 60 \text{ triệu đồng} \] Đáp số: 60 triệu đồng.