Giải hộ mình câu này với các bạn

Câu 8. Để giải bài toán này, ta cần sử dụng tính chất của xác suất của biến cố độc lập. Nếu A và B là hai biến cố độc lập, thì xác suất của biến cố đồng thời xảy ra cả A và B (biến cố AB) được tính bằng tích của xác suất của A và xác suất của B. Công thức là: \[ P(AB) = P(A) \times P(B) \] Trong bài toán này: - Xác suất của biến cố A là \( P(A) = \frac{1}{2} \) - Xác suất của biến cố B là \( P(B) = \frac{1}{4} \) Áp dụng công thức trên, ta có: \[ P(AB) = \frac{1}{2} \times \frac{1}{4} = \frac{1}{8} \] Vậy, xác suất để xảy ra biến cố A và B là: \[ P(AB) = \frac{1}{8} \] Do đó, đáp án đúng là: A. \( P(AB) = \frac{1}{8} \) Câu 9. Để giải quyết bài toán này, chúng ta cần dựa vào tính chất của hàm số mũ và hàm số lôgarit. 1. Hàm số mũ \( y = a^x \): - Nếu \( a > 1 \), đồ thị hàm số \( y = a^x \) sẽ tăng từ trái sang phải. - Nếu \( 0 < a < 1 \), đồ thị hàm số \( y = a^x \) sẽ giảm từ trái sang phải. 2. Hàm số lôgarit \( y = \log_b x \): - Nếu \( b > 1 \), đồ thị hàm số \( y = \log_b x \) sẽ tăng từ trái sang phải. - Nếu \( 0 < b < 1 \), đồ thị hàm số \( y = \log_b x \) sẽ giảm từ trái sang phải. Bây giờ, chúng ta sẽ phân tích đồ thị đã cho: - Đồ thị của hàm số \( y = a^x \) đang tăng từ trái sang phải, do đó \( a > 1 \). - Đồ thị của hàm số \( y = \log_b x \) đang giảm từ trái sang phải, do đó \( 0 < b < 1 \). Từ những phân tích trên, chúng ta có thể kết luận rằng: - \( a > 1 \) - \( 0 < b < 1 \) Do đó, đáp án đúng là: B. \( a > 1; 0 < b < 1 \). Câu 10. 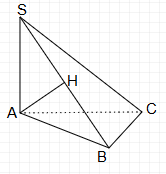Trước tiên, ta xét các khẳng định một cách chi tiết: - Khẳng định A: \( SA \perp BC \) Do \( SA \perp \text{đáy} \), tức là \( SA \perp AB \) và \( SA \perp AC \). Vì \( BC \) nằm trong mặt phẳng đáy, nên \( SA \perp BC \). - Khẳng định B: \( AH \perp BC \) \( AH \) là đường cao của tam giác \( SAB \), do đó \( AH \perp SB \). Mặt khác, vì \( BC \) nằm trong mặt phẳng đáy và \( AH \) nằm trong mặt phẳng \( SAB \), nên \( AH \) không trực tiếp vuông góc với \( BC \). Tuy nhiên, do \( BC \perp AB \) và \( AB \perp SA \), ta có thể suy ra \( BC \perp \text{mặt phẳng} SAB \). Do đó, \( AH \perp BC \). - Khẳng định C: \( AH \perp AC \) \( AH \) là đường cao của tam giác \( SAB \), do đó \( AH \perp SB \). Tuy nhiên, \( AC \) nằm trong mặt phẳng đáy và không trực tiếp liên quan đến \( AH \) trong mặt phẳng \( SAB \). Do đó, \( AH \) không trực tiếp vuông góc với \( AC \). - Khẳng định D: \( AH \perp SC \) \( AH \) là đường cao của tam giác \( SAB \), do đó \( AH \perp SB \). Tuy nhiên, \( SC \) nằm trong mặt phẳng \( SAC \) và không trực tiếp liên quan đến \( AH \) trong mặt phẳng \( SAB \). Do đó, \( AH \) không trực tiếp vuông góc với \( SC \). Từ các lập luận trên, ta thấy rằng khẳng định C và D đều không đúng. Tuy nhiên, trong bốn khẳng định, chỉ có một khẳng định sai. Do đó, khẳng định sai là: C. \( AH \perp AC \) Đáp án: C. \( AH \perp AC \) Câu 11. Để giải quyết bài toán này, chúng ta sẽ sử dụng công thức cường độ động đất \( M = \log A - \log A_0 \). Bước 1: Xác định thông tin đã biết: - Trận động đất ở San Francisco có cường độ \( M_{SF} = 8 \) độ Richter. - Biên độ rung chấn của trận động đất ở Nam Mỹ mạnh hơn gấp 4 lần so với trận động đất ở San Francisco. Bước 2: Áp dụng công thức cường độ động đất: \[ M_{SF} = \log A_{SF} - \log A_0 \] \[ 8 = \log A_{SF} - \log A_0 \] Bước 3: Biên độ rung chấn của trận động đất ở Nam Mỹ là: \[ A_{NamMy} = 4 \times A_{SF} \] Bước 4: Áp dụng công thức cường độ động đất cho trận động đất ở Nam Mỹ: \[ M_{NamMy} = \log A_{NamMy} - \log A_0 \] \[ M_{NamMy} = \log (4 \times A_{SF}) - \log A_0 \] Bước 5: Sử dụng tính chất của logarit để đơn giản hóa: \[ M_{NamMy} = \log 4 + \log A_{SF} - \log A_0 \] Bước 6: Thay giá trị \( \log A_{SF} - \log A_0 \) từ Bước 2 vào: \[ M_{NamMy} = \log 4 + 8 \] Bước 7: Tính giá trị của \( \log 4 \): \[ \log 4 \approx 0,602 \] Bước 8: Kết hợp các giá trị lại: \[ M_{NamMy} = 0,602 + 8 \] \[ M_{NamMy} \approx 8,602 \] Vậy cường độ của trận động đất ở Nam Mỹ gần với số 8,6 nhất. Đáp án đúng là: C. 8,6. Câu 12. 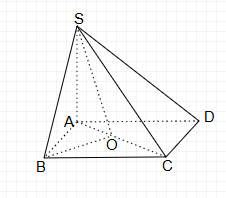Để tính diện tích hình chiếu của $\Delta SBC$ trên mặt phẳng (SAC), ta thực hiện các bước sau: 1. Xác định hình chiếu của điểm B trên mặt phẳng (SAC). Gọi hình chiếu này là B'. Vì SA vuông góc với đáy ABCD, nên B' nằm trên đường thẳng AC. 2. Xác định hình chiếu của đoạn thẳng BC trên mặt phẳng (SAC). Hình chiếu này là đoạn thẳng B'C'. 3. Diện tích hình chiếu của $\Delta SBC$ trên mặt phẳng (SAC) sẽ là diện tích tam giác SB'C'. Ta có: - Tam giác SAC là tam giác vuông tại A. - Tam giác SBC là tam giác vuông tại B. Diện tích tam giác SAC là: \[ S_{SAC} = \frac{1}{2} \times SA \times AC = \frac{1}{2} \times 2a \times \sqrt{(2a)^2 + a^2} = \frac{1}{2} \times 2a \times a\sqrt{5} = a^2\sqrt{5} \] Diện tích tam giác SBC là: \[ S_{SBC} = \frac{1}{2} \times SB \times BC = \frac{1}{2} \times \sqrt{(2a)^2 + (2a)^2} \times \sqrt{(2a)^2 + a^2} = \frac{1}{2} \times 2a\sqrt{2} \times a\sqrt{5} = a^2\sqrt{10} \] Tỉ số diện tích tam giác SB'C' so với tam giác SBC là: \[ \frac{S_{SB'C'}}{S_{SBC}} = \frac{AC}{BC} = \frac{a\sqrt{5}}{a\sqrt{10}} = \frac{\sqrt{5}}{\sqrt{10}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \] Do đó diện tích hình chiếu của $\Delta SBC$ trên mặt phẳng (SAC) là: \[ S_{SB'C'} = S_{SBC} \times \frac{\sqrt{2}}{2} = a^2\sqrt{10} \times \frac{\sqrt{2}}{2} = a^2\sqrt{5} \times \frac{1}{2} = \frac{a^2\sqrt{5}}{2} \] Vậy đáp án đúng là: \[ \boxed{\frac{a^2\sqrt{5}}{2}} \] Câu 1. Để lập luận về các đồ thị hàm số $y = \log_a x$, $y = \log_b x$, $y = \log_c x$ dựa trên hình vẽ, chúng ta sẽ tiến hành như sau: 1. Xác định tính chất của hàm số logarit: - Hàm số $y = \log_a x$ là hàm số lôgarit cơ số $a$. - Nếu $a > 1$, hàm số $y = \log_a x$ là hàm số đồng biến trên $(0, +\infty)$. - Nếu $0 < a < 1$, hàm số $y = \log_a x$ là hàm số nghịch biến trên $(0, +\infty)$. 2. Phân tích đồ thị: - Trên hình vẽ, ta thấy đồ thị $y = \log_a x$ nằm phía trên đồ thị $y = \log_b x$ và $y = \log_c x$ khi $x > 1$. Điều này cho thấy $\log_a x$ tăng nhanh hơn so với $\log_b x$ và $\log_c x$ khi $x > 1$. - Đồ thị $y = \log_b x$ nằm giữa hai đồ thị còn lại, tức là $\log_b x$ tăng chậm hơn $\log_a x$ nhưng nhanh hơn $\log_c x$ khi $x > 1$. - Đồ thị $y = \log_c x$ nằm phía dưới cùng, tức là $\log_c x$ tăng chậm nhất trong ba hàm số khi $x > 1$. 3. So sánh các cơ số: - Vì $\log_a x$ tăng nhanh nhất, nên cơ số $a$ phải lớn nhất trong ba cơ số $a$, $b$, $c$. - Vì $\log_b x$ tăng ở giữa, nên cơ số $b$ phải nằm giữa hai cơ số $a$ và $c$. - Vì $\log_c x$ tăng chậm nhất, nên cơ số $c$ phải nhỏ nhất trong ba cơ số $a$, $b$, $c$. Từ đó, ta có thể kết luận: - $a > b > c$ Đáp số: $a > b > c$